专题18.20平行四边形最短路径问题 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.20平行四边形最短路径问题 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 21:49:13 | ||
图片预览

文档简介
专题18.20 平行四边形最短路径问题(巩固篇)(专项练习)
一、单选题
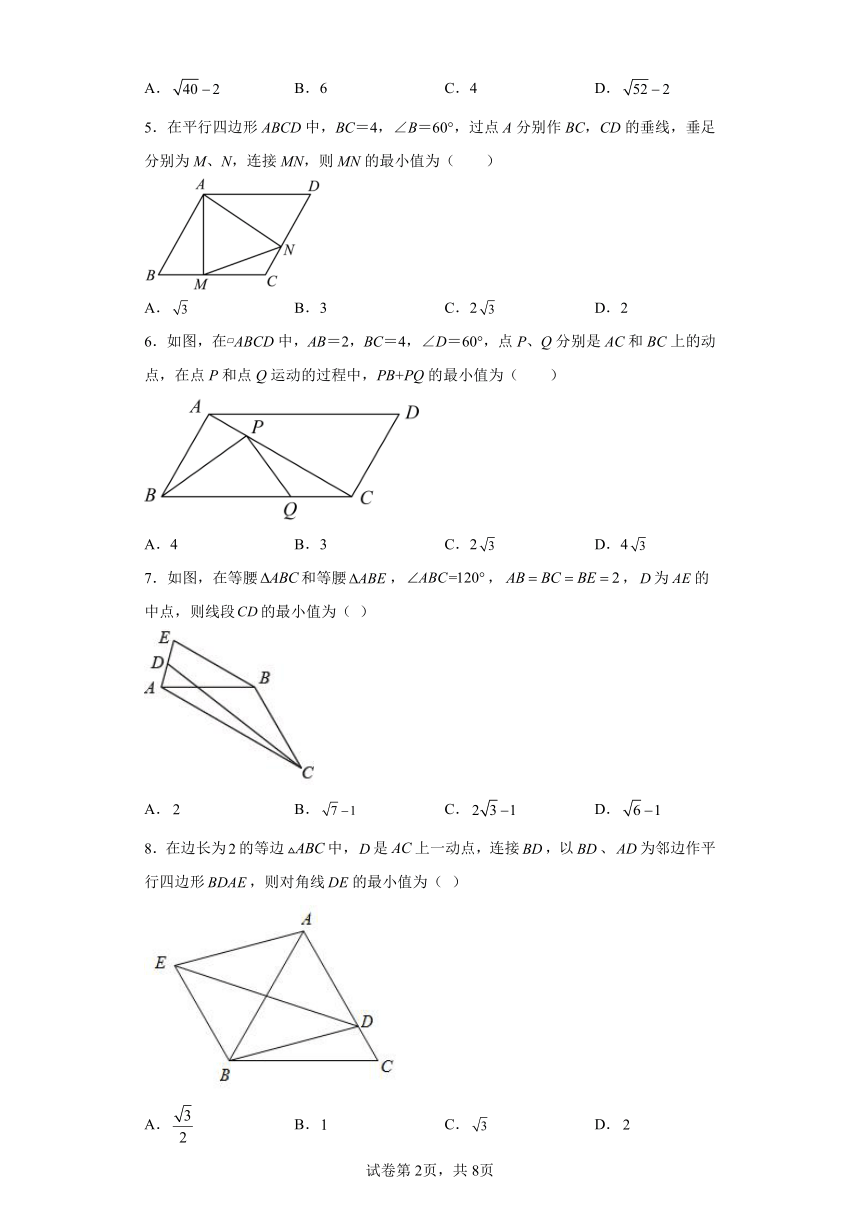
1.如图,△ABC中,∠BAC=45°,AB=AC=8,P为AB边上的一动点,以PA,PC为边作平行四边形PAQC,则线段AQ长度的最小值为( )
A.6 B.8 C. D.
2.如图,在平行四边形ABCD中,,,E是AB的中点,P是边AD上的一动点,若,则的最小值为( )
A. B. C. D.
3.如图,在中,,,,D为AB边上一点,将DC平移到AE(点D与点A对应),连接DE,则DE的最小值为( )
A. B.2 C.4 D.
4.如图,在平行四边形中,,,,是边的中点,是线段上的动点,将沿所在直线折叠得到,连接,则的最小值是( )
A. B.6 C.4 D.
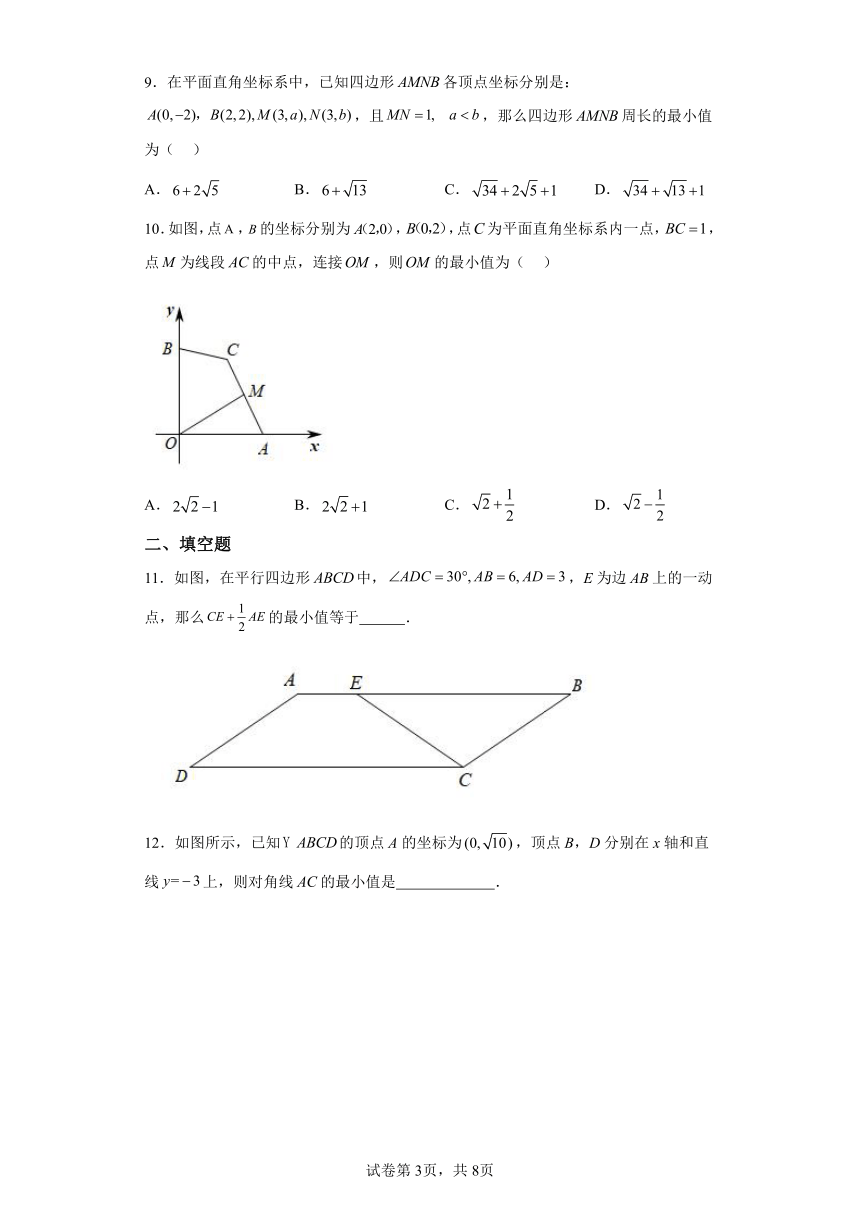
5.在平行四边形ABCD中,BC=4,∠B=60°,过点A分别作BC,CD的垂线,垂足分别为M、N,连接MN,则MN的最小值为( )
A. B.3 C.2 D.2
6.如图,在 ABCD中,AB=2,BC=4,∠D=60°,点P、Q分别是AC和BC上的动点,在点P和点Q运动的过程中,PB+PQ的最小值为( )
A.4 B.3 C.2 D.4
7.如图,在等腰和等腰,,,为的中点,则线段的最小值为( )
A. B. C. D.
8.在边长为的等边中,是上一动点,连接,以、为邻边作平行四边形,则对角线的最小值为( )
A. B. C. D.
9.在平面直角坐标系中,已知四边形各顶点坐标分别是:,且,那么四边形周长的最小值为( )
A. B. C. D.
10.如图,点,的坐标分别为,,点为平面直角坐标系内一点,,点为线段的中点,连接,则的最小值为( )
A. B. C. D.
二、填空题
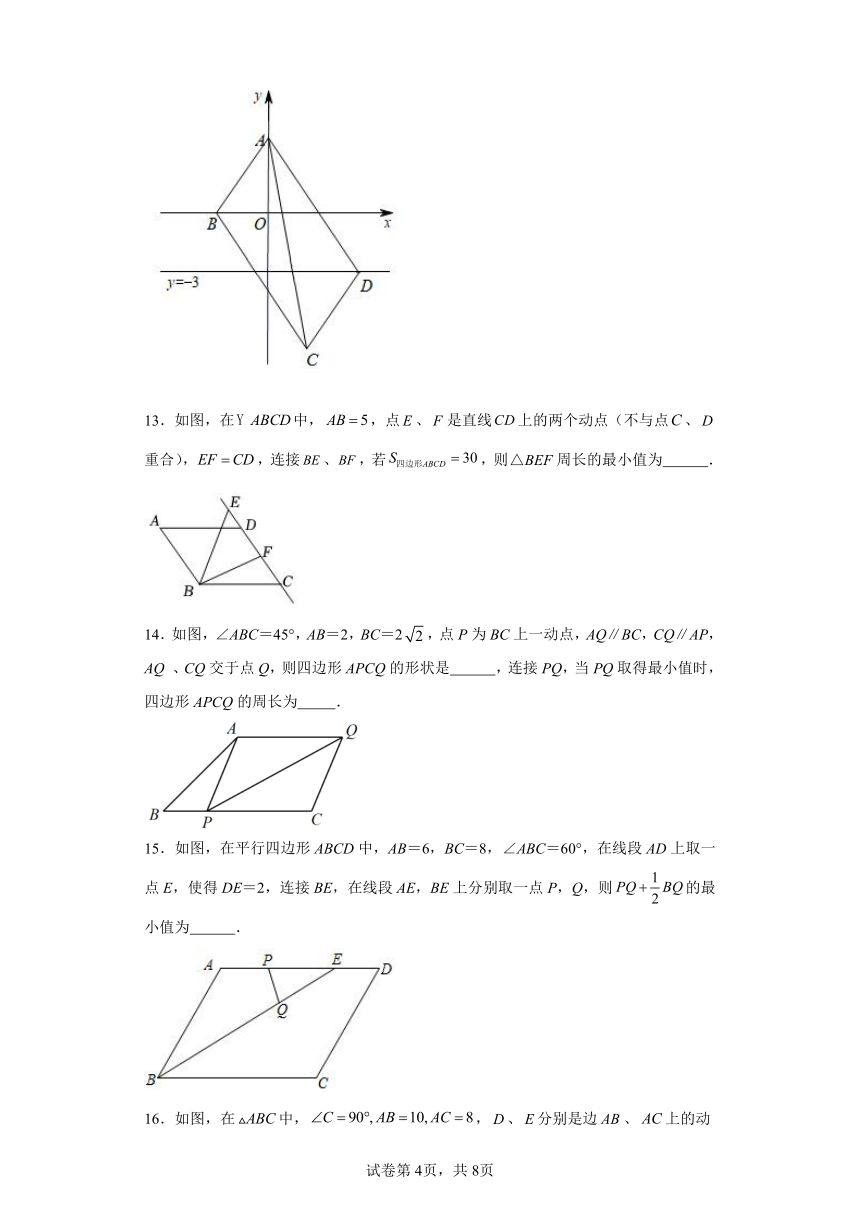
11.如图,在平行四边形中,,E为边上的一动点,那么的最小值等于 .
12.如图所示,已知的顶点A的坐标为,顶点B,D分别在x轴和直线上,则对角线的最小值是 .
13.如图,在中,,点、是直线上的两个动点(不与点、重合),,连接、,若,则周长的最小值为 .
14.如图,∠ABC=45°,AB=2,BC=2,点P为BC上一动点,AQ∥BC,CQ∥AP,AQ 、CQ交于点Q,则四边形APCQ的形状是 ,连接PQ,当PQ取得最小值时,四边形APCQ的周长为 .
15.如图,在平行四边形ABCD中,AB=6,BC=8,∠ABC=60°,在线段AD上取一点E,使得DE=2,连接BE,在线段AE,BE上分别取一点P,Q,则的最小值为 .
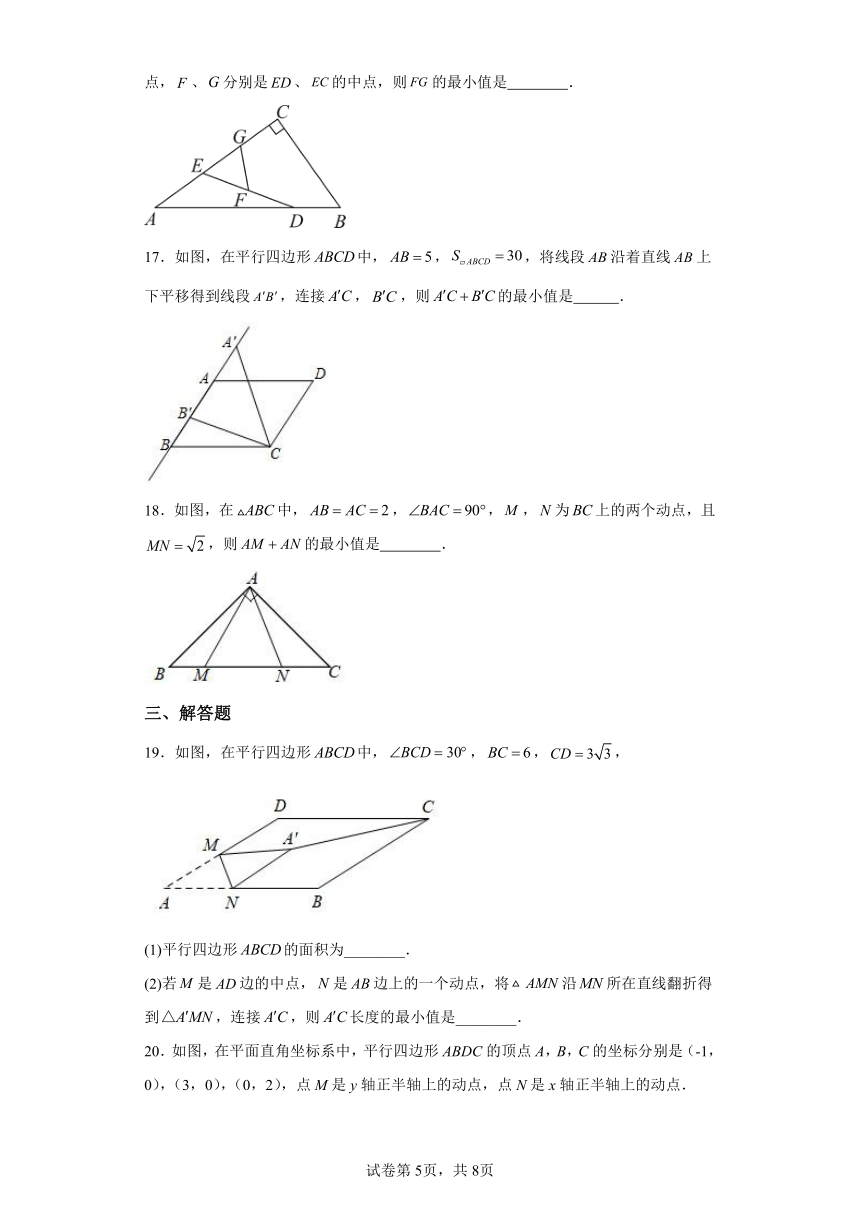
16.如图,在中,,、分别是边、上的动点,、分别是、的中点,则的最小值是 .
17.如图,在平行四边形中,,,将线段沿着直线上下平移得到线段,连接,,则的最小值是 .
18.如图,在中,,,,为上的两个动点,且,则的最小值是 .
三、解答题
19.如图,在平行四边形中,,,,
(1)平行四边形的面积为________.
(2)若是边的中点,是边上的一个动点,将沿所在直线翻折得到,连接,则长度的最小值是________.
20.如图,在平面直角坐标系中,平行四边形ABDC的顶点A,B,C的坐标分别是(-1,0),(3,0),(0,2),点M是y轴正半轴上的动点,点N是x轴正半轴上的动点.
(1)填空:点D的坐标为_______;CN+DN的最小值为_________
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,若四边形OMDB的面积是8,求t的值;
(3)在(2)的条件下,点M从O点出发的同时,点N从点B出发,以每秒2个单位的速度向左平移运动,设射线DN交y轴于点E.设运动时间为t秒.问:S△EMD-S△OEN的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
21.如图,在中,,,动点在的延长线上,是以为斜边的直角三角形,是的中点,连接,,且.
(1)证明:、、三点共线;
(2)连接.
①试判断线段与的数量关系,并给出证明;
②当,且线段取到最小值时,求的长度.
22.如图1,在平面直角坐标系中,点,点,且a,b满足.平移OA至CB(点O与点C对应,点A与点B对应),连接OC,AB.
(1)填空: , ,点B的坐标为 ;
(2)点D,E分别是OA,AB边上的动点,连接DC,DE,M,N分别为DC,DE的中点,连接MN.当D,E分别在OA,AB边上运动时,MN是否存在最小值?若存在,求出MN的最小值;若不存在,请说明理由;
(3)如图2,将线段CO绕点C逆时针旋转90°至CF,连接OF.P为线段OF上一点,以CP为直角边作等腰直角三角形CPQ,其中.试猜想,,三者之间有怎样的数量关系,并证明你的猜想.
23.如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB.
(1)如图1所示,当∠DPA'=10°时,∠A'PB= 度;
(2)如图2所示,当PA'⊥BC时,求线段PA的长度;
(3)当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.
24.在学习完了《18.1平行四边形的性质》之后,王老师在数学活动课上对下面一个问题让学生展开探究活动.
问题情境:图1,在 ABCD中,CA⊥AB,AB=6cm,AC=8cm,点O为AC的中点,动点P在BC边上运动,直线PO交AD于E.
问题发现:数学智慧小组”通过积极的动手操作,观察,猜想,提出了如下问题:
(1)在点P运动的过程中,始终存在PO=OE,为什么?
(2)在点P运动到PO⊥AC时,四边形ABPE是平行四边形,为什么?此时BP的长度是多少?
(3)在点P运动的过程中,四边形ABPE的周长是否存在最小值?如果存在,则四边形ABPE的周长的最小值是 cm;BP的长度为 cm.
问题解决:
“数学智慧小组”欢迎您的加入,请开启您的“问题解决之旅”吧!
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据平行四边形的性质,垂线段最短,可以得到当CP⊥AB时,CP取得最小值,此时CP的值就是AQ的最小值,从而可以解答本题.
【详解】解:∵四边形PAQC是平行四边形,
∴AQ=PC,
∴要求AQ的最小值,只要求PC的最小值即可,
∴当CP⊥AB时,CP取得最小值,
∵∠BAC=45°,
,
设,
在Rt△APC中,AB=AC=8,
则,即,
解得,
故选:D.
【点睛】本题考查平行四边形的性质、等腰三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
2.C
【分析】由得∠ADB=90°,由勾股定理求出BD=2,得到∠BAD=∠ABD=45°,延长BD至点,使得 D=BD=2,连接E,则点P在E与AD的交点时,PE+PB的值最小,给出证明,再过点E作EF⊥B于点F,由勾股定理求出EF的长,再求得F=BD+D-BE=3,最后利用勾股定理得出答案.
【详解】解:∵
∴∠ADB=90°
∵,
∴AB=2
由勾股定理得
BD=
∴AD=BD=2
∴∠BAD=∠ABD=45°
∵E是AB的中点,
∴BE=AE=AB=
延长BD至点,使得 D=BD=2,连接E,
则点P在E与AD的交点时,PE+PB的值最小,如下图,
理由如下:
∵ ’ ,D=BD=2,
∴ AD垂直平分B
∴AD上任意一点P,总有PB=P,
由“两点之间,线段最短”可知,点P在E与AD的交点处时,
PE+PB的值最小,最小值为E的长,此时过点E作EF⊥B于点F,如上图,
则∠EFB=∠EF=90°,
∵∠ABD=45°
∴EF=BF
∴EF2+BF2=BE2=2EF2
∴EF=BF==1
∴F=BD+D-BE=3
在Rt△EF中,由勾股定理得
E===
即的最小值为
故选:C
【点睛】本题考查了最短路径问题、勾股定理、等腰直角三角形等知识点,掌握最短路径的确定方法、灵活应用勾股定理是解题的关键.
3.A
【分析】过点C作CG⊥AB于点G,连接CE,根据,,,运用勾股定理的逆定理,证明△ABC是直角三角形,得到∠ACB=90°,根据平移性质证明四边形ADEC是平行四边形,得到CE∥AD,根据当DE⊥AB时, DE最小,此时,根据∠DEC=∠ECG=90°,证明四边形EDGC是矩形,得到DE=CG,运用面积法得到,求出,得到DE的最小值为.
【详解】过点C作CG⊥AB于点G,连接CE,
则∠AGC=90°,
∵中,,,,
∴,
∴是直角三角形,∠ACB=90°,
由平移知,AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
∴CE∥AD,
当DE⊥AB时, DE最小,
此时,∠DEC=∠ECG=90°,
∴四边形EDGC是矩形,
∴DE=CG,
∵
∴
∴,
∴,
∴DE的最小值为.
故选A.
【点睛】本题主要考查了勾股定理的逆定理,平移,平行四边形,三角形面积,垂线段,解决问题的关键是添加辅助线,熟练掌握用勾股定理的逆定理判断直角三角形,平移的性质,平行四边形的判定和性质,三角形面积公式,垂线段最短的性质.
4.D
【分析】点的运动轨迹以E为圆心,以AE的长为半径的圆,则当点落在DE上时,取最小值,根据折叠的性质利用勾股定理即可求解.
【详解】解:点的运动轨迹以E为圆心,以AE的长为半径的圆,则当点落在DE上时,取最小值,如图所示:
∵AB=4,E是AB边的中点,
∴AE=BE=2,
由沿所在直线折叠得到,
∴,
在平行四边形ABCD中,
∵∠B=60°,
∴∠BEG=∠AEH=30°,
∴BG=AH=1,
,
∴DH=AD=AH=6+1=7,
在Rt△DHE中,由勾股定理得:
,
∴,
∴的最小值是,
故选:D.
【点睛】本题考查了折叠的性质,平行四边形的性质,两点之间线段最短的综合应用,勾股定理,含30°角的直角三角形,确定点的位置,利用勾股定理解决问题是解题的关键.
5.B
【分析】由平行四边形的性质和直角三角形的性质可求FC,AN,EN,AE的长,即可求解.
【详解】解:如图,过点C作CF⊥AB于点F,过点N作NE⊥AD于E,
∵四边形ABCD是平行四边形,
∴,∠B=∠D=60°,
∵CF⊥AB,AN⊥CD,
∴,∠BCF=30°,
∴四边形AFCN是平行四边形,BFBC=2,CFBF=2,
∴AN=CF=2,
∵AN⊥CD,∠D=60°,
∴∠NAD=30°,
∴ENAN,AEEN=3,
∵AM⊥BC,NE⊥AD,
∴,
∴当MN⊥EN时,MN有最小值为3,
故选:B.
【点睛】本题考查了平行四边形的性质,直角三角形的性质,添加恰当辅助线构造直角三角形是解题的关键.
6.C
【分析】取BC的中点G,连接AG.首先证明∠BAC=90°,作点B关于AC的对称点F,连接GF,证FG⊥BC,则FG的长即为PB+PQ的最小值.
【详解】解:取BC的中点G,连接AG.在 ABCD中,AB=2,BC=4,∠D=60°,
∴AB=BG=2,∠ABG=∠D=60°,
∴△ABG是等边三角形,
∴AG=GC=2,∠AGB=∠BAG=60°,
∴∠GAC=∠GCA=30°,
∴∠BAC=90°,
作点B关于AC的对称点F,连接GF, 交AC于点P,由对称可知,B、A、F在一条直线上,AG=AF,
∵∠BAG=∠F+∠AGF=60°,
∴∠F=∠AGF=30°,
∴∠FGB=90°,
当点Q与点G重合时,PB+PQ=PF+PG=FG,FG的长即为PB+PQ的最小值,
∵∠F=∠AGF=30°,AG=GC=2,
∴BF=4,
,
∴BP+PQ的最小值为2.
故选:C.
【点睛】本题主要考查了轴对称﹣最短路线问题,勾股定理,等边三角形的性质,根据垂线段最短作出辅助线,确定点P,Q的位置是解答此题的关键.
7.B
【分析】取AB的中点G,接DG,CG,过C作于点H,根据三角形中位线的性质和勾股定理解答即可.
【详解】解:取AB得中点G,连接DG,CG,过点C作交AB延长线与H.
∵点D是AE的中点,点G是AB的中点,
∴AD = ED,AG=BG,
∴DG是的中位线,
∴DG=BE,
∵AB=BC=BE=2,
∴DG=1,BG=1,
∵,
∴,
∵,
∴,,
∴,
∴,
∴HG= BG +BH=2,
在中,
,
∵,
∴,
∴当且仅当D、G、C三点共线时,线段CD取最小值为.
故选:B.
【点睛】此题考查勾股定理,关解题的键是根据三角形的中位线定理和勾股定理解答.
8.C
【分析】根据平行四边形的性质可推出DE=2OD,则可得当OD⊥AC时,DO的值最小,即DE的值最小,过O作OF⊥AC于点F,利用等边三角形及直角三角形性质可求得AF=OA=,则可利用勾股定理求得OF的长,即可得出结论.
【详解】解:设AB与DE相交于点O,
∵四边形是平行四边形,是边长为2的等边三角形,
∴OA=OB=AB=1,OD=OE=DE.
即DE=2OD.
∴当OD⊥AC时,DO的值最小,即DE的值最小.
如图,过O作OF⊥AC于点F,
∴∠AFO =90°.
∵是等边三角形,
∴∠BAC =60°.
∴∠AOF =30°.
∴AF=OA=.
∴OF=.
当OD=OF时,DO的值最小,即DE的值最小,
∴DE=2OF=.
故选:C.
【点睛】此题考查了平行四边形、等边三角形及直角三角形的性质等知识,熟练掌握平行四边形的性质是解题的关键.
9.A
【分析】如图,把向上平移一个单位得:,作关于直线的对称点 连接,交直线于 连接,则此时四边形的周长最短,再利用勾股定理可得: ,利用从而可得答案.
【详解】解:如图,把向上平移一个单位得:,作关于直线的对称点 连接,交直线于 连接,
,
由
四边形是平行四边形,
所以此时:四边形的周长最短,
故选:
【点睛】本题考查的是图形与坐标,勾股定理的应用,轴对称的性质,平行四边形的判定与性质,掌握以上知识是解题的关键.
10.D
【分析】连接,取中点,连接,根据三角形任意两边之和大于第三边求最值即可.
【详解】解:连接,取中点,连接,
∵,
∴当取最大值时,三点共线,即在之间,
即,
∵分别是的中点,
∴,
∵,
∴,
∴,
∴,
故选:D.
【点睛】本题考查三角形的三边关系,中位线定理,平面直角坐标系中的点与几何,勾股定理,能够熟练掌握数形结合思想是解决本题的关键.
11.3
【分析】如图,过作交的延长线于点,根据平行四边形的性质,推出,从而得到,进而得到,根据,可知,当三点共线时,线段的和最小,利用所对的直角边是斜边的一半即可得解.
【详解】解:如图,过作交的延长线于点,
∵四边形为平行四边形,
∴,
∴,
∴,
∴,
∵,
∴当三点共线时,线段的和最小,
∵,,
∴,
即:的最小值等于3;
故答案为:3.
【点睛】本题考查平行四边形的性质,以及含的直角三角形.通过添加辅助线,构造含的直角三角形,利用垂线段最短进行求解,是解题的关键.本题是胡不归模型,平时多归纳总结,可以快速解题.
12.##
【分析】设点C坐标为(a,b),由平行四边形的性质可求b=,可得点C在直线y=上运动,再根据点C在y轴上时,AC的长度有最小值求解即可.
【详解】解:设点C坐标为(a,b),
∵顶点B、D分别在x轴和直线y= 3上,
∴点B,点D的纵坐标分别为0, 3,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴,
∴b=,
∴点C在直线y=上运动,
∴当点C在y轴上时,AC的长度有最小值,
∴对角线AC的最小值为:,
故答案为:.
【点睛】本题考查了平行四边形的性质,坐标与图形性质,确定点C的运动轨迹是本题的关键.
13.18
【分析】作点E关于AB的对称点G,连接EG交AB于点H,连接BG,FG,则EG⊥AB,GH=EH,BE=BG,可得当点G,B,F三点共线时,BG+BF最小,即为FG的长,此时周长的最小,再根据平行四边形的性质可得,GH=EH=6,进而得到EG=12,再由勾股定理,即可求解.
【详解】解:如图,作点E关于AB的对称点G,连接EG交AB于点H,连接BG,FG,则EG⊥AB,GH=EH,BE=BG,
∴周长为BE+BF+EF=BG+BF+EF,
∴当点G,B,F三点共线时,BG+BF最小,即为FG的长,此时周长的最小,
四边形是平行四边形,
,,
∴EG⊥CD,
,
∴,
∴GH=EH=6,
∴EG=12,
∴,
的最小值为,
的周长的最小值为,
故答案为:.
【点睛】本题考查轴对称最短问题,解题的关键是熟练掌握平行四边形的性质,勾股定理,属于中考常见题.
14. 平行四边形 ##
【分析】根据两组对边分别平行的四边形是平行四边形即可求解;当PQ是AQ和BC间距离时PQ取得最小值,计算四边形APCQ的周长即可.
【详解】解:如图,∵AQBC,CQAP,
∴四边形APCQ是平行四边形.
当PQ⊥BC时,PQ取得最小值,
∵四边形APCQ是平行四边形,
∴AH=HC=AC,QH=PH=PQ,
∵∠ABC=45°,AB=2,BC=,
∴AC=2,∠ACB=45°,
∵QP⊥BC,
∴∠PHC=45°,
∴PH=PC=,
∴PQ=,
∴QC=,
∴四边形APCQ的周长为:2PC+2QC=2×+2×=,
故答案为:平行四边形;.
【点睛】本题主要考查了平行四边形的性质,等腰三角形的判定,垂线段最短的性质,综合性较强.
15.
【分析】根据平行四边形的性质可得∠EBC=30°,过点Q作QM⊥BC于点M,过点P作PN⊥BC于点N,过点A作AH⊥BC于点H,根据含30°角的直角三角形的性质可得QM=BQ,PQ+BQ最小值即为PN的长,根据平行线之间的距离相等,可得PN=AH,根据勾股定理求出AH的长即可.
【详解】解:在平行四边形ABCD中,AD∥BC,AD=BC,
∴∠AEB=∠EBC,
∵AB=6,BC=8,DE=2,
∴AE=8-2=6,
∴AE=AB,
∴∠AEB=∠ABE,
∴∠ABE=∠EBC,
∵∠ABC=60°,
∴∠EBC=30°,
过点Q作QM⊥BC于点M,过点P作PN⊥BC于点N,过点A作AH⊥BC于点H,如图所示:
则QM=BQ,
∴PQ+BQ最小值即为PN的长,
∵AD∥BC,
∵PN=AH,
∵∠BAH=30°,AB=6,
∴BH=3,
根据勾股定理,可得AH=PN=,
∴PQ+BQ的最小值为,
故答案为:.
【点睛】本题考查了平行四边形的性质,直角三角形的性质,勾股定理等,通过构造直角三角形,找出PQ+BQ最小值即为PN的长是解题的关键.
16.
【分析】连接CD,根据三角形中位线的性质定理得出FG=,由勾股定理求出BC,再根据三角形等面积法求出CD,即可得出结果.
【详解】解:连接CD,
∵F、G分别是ED、EC的中点,
∴FG是△FDC的中位线,
∴FG=,
当CD最小时,FG最小,
当CD⊥AB时,CD最小,
在△ABC中,∠C=90°,AB=10,AC=8,
则BC=,
当CD⊥AB时,
,
∴,
解得:CD=,
∴FG的最小值为,
故答案为:.
【点睛】题目主要考查三角形中位线定理,勾股定理解三角形,垂线段最短,掌握三角形中位线定理是解题关键.
17.13
【分析】先由平移性质证明四边形为平行四边形,从而得,进而使得,再作关于直线的对称点,由对称性得,再由,求出,,由勾股定理求出即可.
【详解】解:连接,
由平移性质得:,,
四边形为平行四边形,
,
,
作关于直线的对称点,连接,,交延长线于,
由对称性得:,,,
,
,,
,
,,
,
,
,
的最小值为,
故答案为:
【点睛】本题主要考查了平行四边形的判定与性质、最短路径问题、勾股定理,解决此题的关键是证明四边形为平行四边形、再作关于直线的对称点,将的最小值转化为.
18.
【分析】过点A作AD//BC,且AD=MN,连接MD,则四边形ADMN是平行四边形,作点A关于BC的对称点A′,连接AA′交BC于点O,连接A′M,三点D、M、A′共线时,最小为A′D的长,利用勾股定理求A′D的长度即可解决问题.
【详解】解:过点A作AD//BC,且AD=MN,连接MD,
则四边形ADMN是平行四边形,
∴MD=AN,AD=MN,
作点A关于BC的对称点A′,连接A A′交BC于点O,连接A′M,
则AM=A′M,
∴AM+AN=A′M+DM,
∴三点D、M、A′共线时,A′M+DM最小为A′D的长,
∵AD//BC,AO⊥BC,
∴∠DA=90°,
∵,,,
∴BC=
BO=CO=AO=,
∴,
在Rt△AD中,由勾股定理得:
D=
∴的最小是值为:,
故答案为:
【点睛】本题主要考查了等腰三角形的性质,平行四边形的判定与性质,勾股定理等知识,构造平行四边形将AN转化为DM是解题的关键.
19.(1)
(2)
【分析】(1)过点作,交延长线于,根据平行四边形的性质得出,,根据含度角的直角三角形的性质得出,进而求得四边形的面积;
(2)连接,过点作于,交的延长线于点,根据轴对称的性质,以及两点直线线段最短可得到,当折线与线段重合时,线段的长度最短,根据勾股定理即可求解.
【详解】(1)解:过点作,交延长线于,
四边形是平行四边形,
,,,
,
,
四边形的面积;
故答案为:;
(2)连接,过点作于,交的延长线于点;
四边形为平行四边形,
,,
点为的中点,,
,,
,,
,
由勾股定理得:,
,
由翻折变换的性质得:,
,
,当折线与线段重合时,线段的长度最短,
此时,
故答案为:.
【点睛】本题考查了平行四边形的性质,含30度角的直角三角形的性质,勾股定理,轴对称求线段最值问题,掌握轴对称的性质是解题的关键.
20.(1)(4,2),4
(2)t的值是;
(3))S△EMD-S△OEN的值不会发生变化,S△EMD-S△OEN的值是3.
【分析】(1)作C(0,2)关于x轴的对称点C'(0,-2),连接DC'交x轴于N,此时CN+DN最小,最小值为C'D的长,由A(-1,0),B(3,0),四边形ABDC是平行四边形,可得DC=AB=4,D(4,2),在Rt△DCC'中,利用勾股定理求得DC'=4,即得CN+DN的最小值为4;
(2)根据S四边形OCDB=7,四边形OMDB的面积是8,知M在C的上方,且S△CDM=8-7=1,故CM DC=1,即(t-2)×4=1,可解得t的值;
(3)连接OD,由S△EMD-S△OEN=S△MOD+S△NOD=OM CD+ON OC=3,可得S△EMD-S△OEN的值是3,不会变化.
【详解】(1)解:作C(0,2)关于x轴的对称点C'(0,-2),连接DC'交x轴于N,此时CN+DN最小,最小值为C'D的长,如图:
∵A(-1,0),B(3,0),
∴AB=4,
∵四边形ABDC是平行四边形,
∴DC=AB=4,
∴D(4,2),
在Rt△DCC'中,
DC'=,
∴CN+DN的最小值为4,
故答案为:(4,2),4;
(2)解:如图:
∵S四边形OCDB=×(4+3)×2=7,
又四边形OMDB的面积是8,
∴M在C的上方,且S△CDM=8-7=1,
∴CM DC=1,
即(t-2)×4=1,
解得t=,
答:t的值是;
(3)解:S△EMD-S△OEN的值不会发生变化,理由如下:
连接OD,如图:
∵S△EMD-S△OEN=S四边形MOND,
∴S△EMD-S△OEN
=S△MOD+S△NOD
=OM CD+ON OC
=t×4+(3-2t)×2
=2t+3-2t
=3,
∴S△EMD-S△OEN的值是3,不会变化.
【点睛】本题考查四边形综合应用,涉及平移的性质、轴对称的性质,坐标与图形性质、平行四边形的性质、三角形面积等知识;熟练掌握平移的性质是解题的关键.
21.(1)见解析;
(2)①EC=OA,证明见解析;②.
【分析】(1)证明∠AFE+∠AFB=180°,可得结论;
(2)①结论:EC=AO.连接EO,OC,证明△EOC是等腰直角三角形,可得结论;
②如图2中,取AE的中点J,连接OJ.证明OJ∥EB,推出OF⊥OJ时,OF的值最小,此时四边形OFEJ是矩形,利用勾股定理求出OA,可得结论.
【详解】(1)证明:∵∠AEF=90°,AE=EF,
∴∠EAF=∠EFA=45°,
∵2∠CBF+∠EAF=135°,
∴∠CBF=45°,
∵∠C=90°,
∴∠CFB=90°-45°=45°,
∴∠CFB=∠AFE,
∵∠CFB+∠AFB=180°,
∴∠AFE+∠AFB=180°,
∴E、F、B共线.
(2)解:①结论:EC=OA.
理由:如图1中,连接EO,CO.
∵∠AEB=∠ACB=90°,OA=OB,
∴OE=OA=OB=OC,
∴∠OAC=∠OCA,∠OEB=∠OBE,
∵∠BOC=∠OAC+∠OCA=2∠OCA,∠AOE=∠OEB+∠OBE=2∠OBE,
∴∠BOC+∠AOE=2∠CAO+2∠OBE=2(∠OAC+∠OBE)=2∠CFB=90°,
∴∠EOC=90°,
∴△EOC是等腰直角三角形,
∴EC=EO=OA;
②如图2中,取AE的中点J,连接OJ.
∵AJ=EJ,AO=OB,
∴OJ∥EB,
∴OF⊥OJ时,OF的值最小,此时四边形OFEJ是矩形,
∴EF=AE=OJ=2,AJ=EJ=1,
∴,
∴EC=OA=.
【点睛】本题属于三角形综合题,考查了等腰直角三角形的性质和判定,勾股定理,三角形中位线定理,垂线段最短等知识,解题的关键是学会添加常用辅助线,构造等腰直角三角形解决问题.
22.(1)6,4,(9,4)
(2)存在,
(3),证明见解析
【分析】(1)根据二次根式有意义的条件和绝对值的意义求解即可;
(2)连接CE,根据中位线定理可知MN=CE,当时,CE有最小值,根据三角形面积可求CE的值,即可求解;
(3)连接QF,可证△OCP≌△FCQ,得OP=QF,在直角三角形QFP中,,可求解.
【详解】(1)解:∵,,,
∴,
∴6-a=0,b-4=0,
∴a=6,b=4.
∴点B的坐标为(9,4).
故答案为:6,4,(9,4).
(2)解:MN存在最小值,理由是:
连接CE,如图1,
∵M、N分别是CD、DE的中点,
∴MN=CE.
当时,CE有最小值,
∵C(3,4),A(6,0),
∴OA=6,AB=OC=5,
∴,
∴MN=.
(3)解:连接QF,如图2,
由旋转可知,OC=OF,∠OCF=90°,∠O=∠CFO=45°.
∵△CPQ为等腰直角三角形CPQ,
∴CP=CQ,∠PCQ=90°,∠QCP=45°,
∴∠OCF=∠PCQ,
∴∠OCF-∠PCF=∠PCQ-∠PCF,
即∠OCP=∠FCQ,
在△OCP和△FCQ中,
∴△OCP≌△FCQ(SAS),
∴OP=QF,
∠QFP=∠QFC+∠CFO=45°+45°=90°,
∴,
∵OP=QF,
∴
【点睛】本题考查了全等三角形的判定与性质、三角形的中位线、勾股定理等知识,熟练掌握这些知识是解题的关键.
23.(1)85
(2)5+5
(3)2+2
【分析】(1)根据平角的定义,翻折的性质求解即可;
(2)作BH⊥AD于H.勾股定理解Rt△ABH,由四边形ABCD是平行四边形,AD∥BC,可得∠APA′=90°,PH=BH,根据PA=AH+PH 即可求解;
(3)作BH⊥AD于H,连接BP.勾股定理求得PB,当BA′的长度最小时,△BFA′的周长最小,由BA′≥PB﹣PA′,求得,然后即可求得△BFA′的周长的最小值.
【详解】(1)如图1中,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:∠A′PB=∠APB=×170°=85°.
故答案为85.
(2)如图2中,作BH⊥AD于H.
在Rt△ABH中,∵∠AHB=90°,AB=10,∠A=60°,
∴AH=5,BH=5,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∴PH=BH=5,
∴PA=AH+PH=5+5.
(3)如图3中,作BH⊥AD于H,连接BP.
∵PA=8,AH=5,
∴PH=8﹣5=3,
∵BH=5,
∴PB===2,
由翻折可知:PA=PA′=8,FA=FA′,
∴△BFA′的周长=FA′+BF+BA′=AF+BF+BA′=AB+BA′=10+BA′,
∴当BA′的长度最小时,△BFA′的周长最小,
∵BA′≥PB﹣PA′,
∴BA′≥2﹣8,
∴BA′的最小值为2﹣8,
∴△BFA′的周长的最小值为10+2﹣8=2+2.
【点睛】本题考查了勾股定理解直角三角形,平行四边形的性质,折叠的性质,轴对称求线段和最值问题,综合运用以上知识是解题的关键.
24.(1)见解析;(2)四边形ABPE是平行四边形,理由见解析,BP =5cm;(3),
【分析】(1)证明△AEO△CPO即可说明PO=OE;
(2)证明EP∥AB,即可证明四边形ABPE是平行四边形,利用三角形中位线定理即可求解;
(3)求得四边形ABPE的周长为:6+10+PE=16+PE,得到当PE⊥BC时,PE最小,利用平行四边形的面积公式求得PE,即可求得四边形ABPE的周长最小值,根据△AEO△CPO以及勾股定理即可求得BP的长度.
【详解】(1)证明:∵四边形ABCD是平行四边形,点O为AC的中点,
∴AE∥PC,AO=OC,
∴∠EAO=∠PCO,∠AOE=∠COP,
∴△AEO△CPO,
∴PO=OE;
(2)∵CA⊥AB,且PO⊥AC,
∴PO∥AB,即EP∥AB,
∵四边形ABCD是平行四边形,
∴AE∥BP,
∵CA⊥AB,且AB=6cm,AC=8cm,
∴BC=(cm),
∴四边形ABPE是平行四边形,
∵点O为AC的中点,且PO∥AB,
∴BP=PC=BC=5(cm);
(3)四边形ABPE的周长为:AB+BP+PE+AE,
由(1)知△AEO△CPO,则AE=CP,
∴BP+AE=BP+CP=BC=10,
∴四边形ABPE的周长为:6+10+PE=16+PE,
则PE最小时,四边形ABPE的周长最小,
∴当PE⊥BC时,PE最小(垂线段最短),
∵BCPE=ABAC,
∴PE=(cm),
∴四边形ABPE的周长最小值为16+=(cm),
∵△AEO△CPO,
∴PO=EO=PE=(cm),OC=AC=(cm),
∴PC=(cm),
∴BP=BC-PC=(cm),
故答案为:,.
.
【点睛】本题考查了平行四边形的判定和性质,三角形中位线定理,全等三角形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,△ABC中,∠BAC=45°,AB=AC=8,P为AB边上的一动点,以PA,PC为边作平行四边形PAQC,则线段AQ长度的最小值为( )
A.6 B.8 C. D.
2.如图,在平行四边形ABCD中,,,E是AB的中点,P是边AD上的一动点,若,则的最小值为( )
A. B. C. D.
3.如图,在中,,,,D为AB边上一点,将DC平移到AE(点D与点A对应),连接DE,则DE的最小值为( )
A. B.2 C.4 D.
4.如图,在平行四边形中,,,,是边的中点,是线段上的动点,将沿所在直线折叠得到,连接,则的最小值是( )
A. B.6 C.4 D.
5.在平行四边形ABCD中,BC=4,∠B=60°,过点A分别作BC,CD的垂线,垂足分别为M、N,连接MN,则MN的最小值为( )
A. B.3 C.2 D.2
6.如图,在 ABCD中,AB=2,BC=4,∠D=60°,点P、Q分别是AC和BC上的动点,在点P和点Q运动的过程中,PB+PQ的最小值为( )
A.4 B.3 C.2 D.4
7.如图,在等腰和等腰,,,为的中点,则线段的最小值为( )
A. B. C. D.
8.在边长为的等边中,是上一动点,连接,以、为邻边作平行四边形,则对角线的最小值为( )
A. B. C. D.
9.在平面直角坐标系中,已知四边形各顶点坐标分别是:,且,那么四边形周长的最小值为( )
A. B. C. D.
10.如图,点,的坐标分别为,,点为平面直角坐标系内一点,,点为线段的中点,连接,则的最小值为( )
A. B. C. D.
二、填空题
11.如图,在平行四边形中,,E为边上的一动点,那么的最小值等于 .
12.如图所示,已知的顶点A的坐标为,顶点B,D分别在x轴和直线上,则对角线的最小值是 .
13.如图,在中,,点、是直线上的两个动点(不与点、重合),,连接、,若,则周长的最小值为 .
14.如图,∠ABC=45°,AB=2,BC=2,点P为BC上一动点,AQ∥BC,CQ∥AP,AQ 、CQ交于点Q,则四边形APCQ的形状是 ,连接PQ,当PQ取得最小值时,四边形APCQ的周长为 .
15.如图,在平行四边形ABCD中,AB=6,BC=8,∠ABC=60°,在线段AD上取一点E,使得DE=2,连接BE,在线段AE,BE上分别取一点P,Q,则的最小值为 .
16.如图,在中,,、分别是边、上的动点,、分别是、的中点,则的最小值是 .
17.如图,在平行四边形中,,,将线段沿着直线上下平移得到线段,连接,,则的最小值是 .
18.如图,在中,,,,为上的两个动点,且,则的最小值是 .
三、解答题
19.如图,在平行四边形中,,,,
(1)平行四边形的面积为________.
(2)若是边的中点,是边上的一个动点,将沿所在直线翻折得到,连接,则长度的最小值是________.
20.如图,在平面直角坐标系中,平行四边形ABDC的顶点A,B,C的坐标分别是(-1,0),(3,0),(0,2),点M是y轴正半轴上的动点,点N是x轴正半轴上的动点.
(1)填空:点D的坐标为_______;CN+DN的最小值为_________
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,若四边形OMDB的面积是8,求t的值;
(3)在(2)的条件下,点M从O点出发的同时,点N从点B出发,以每秒2个单位的速度向左平移运动,设射线DN交y轴于点E.设运动时间为t秒.问:S△EMD-S△OEN的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
21.如图,在中,,,动点在的延长线上,是以为斜边的直角三角形,是的中点,连接,,且.
(1)证明:、、三点共线;
(2)连接.
①试判断线段与的数量关系,并给出证明;
②当,且线段取到最小值时,求的长度.
22.如图1,在平面直角坐标系中,点,点,且a,b满足.平移OA至CB(点O与点C对应,点A与点B对应),连接OC,AB.
(1)填空: , ,点B的坐标为 ;
(2)点D,E分别是OA,AB边上的动点,连接DC,DE,M,N分别为DC,DE的中点,连接MN.当D,E分别在OA,AB边上运动时,MN是否存在最小值?若存在,求出MN的最小值;若不存在,请说明理由;
(3)如图2,将线段CO绕点C逆时针旋转90°至CF,连接OF.P为线段OF上一点,以CP为直角边作等腰直角三角形CPQ,其中.试猜想,,三者之间有怎样的数量关系,并证明你的猜想.
23.如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB.
(1)如图1所示,当∠DPA'=10°时,∠A'PB= 度;
(2)如图2所示,当PA'⊥BC时,求线段PA的长度;
(3)当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.
24.在学习完了《18.1平行四边形的性质》之后,王老师在数学活动课上对下面一个问题让学生展开探究活动.
问题情境:图1,在 ABCD中,CA⊥AB,AB=6cm,AC=8cm,点O为AC的中点,动点P在BC边上运动,直线PO交AD于E.
问题发现:数学智慧小组”通过积极的动手操作,观察,猜想,提出了如下问题:
(1)在点P运动的过程中,始终存在PO=OE,为什么?
(2)在点P运动到PO⊥AC时,四边形ABPE是平行四边形,为什么?此时BP的长度是多少?
(3)在点P运动的过程中,四边形ABPE的周长是否存在最小值?如果存在,则四边形ABPE的周长的最小值是 cm;BP的长度为 cm.
问题解决:
“数学智慧小组”欢迎您的加入,请开启您的“问题解决之旅”吧!
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据平行四边形的性质,垂线段最短,可以得到当CP⊥AB时,CP取得最小值,此时CP的值就是AQ的最小值,从而可以解答本题.
【详解】解:∵四边形PAQC是平行四边形,
∴AQ=PC,
∴要求AQ的最小值,只要求PC的最小值即可,
∴当CP⊥AB时,CP取得最小值,
∵∠BAC=45°,
,
设,
在Rt△APC中,AB=AC=8,
则,即,
解得,
故选:D.
【点睛】本题考查平行四边形的性质、等腰三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
2.C
【分析】由得∠ADB=90°,由勾股定理求出BD=2,得到∠BAD=∠ABD=45°,延长BD至点,使得 D=BD=2,连接E,则点P在E与AD的交点时,PE+PB的值最小,给出证明,再过点E作EF⊥B于点F,由勾股定理求出EF的长,再求得F=BD+D-BE=3,最后利用勾股定理得出答案.
【详解】解:∵
∴∠ADB=90°
∵,
∴AB=2
由勾股定理得
BD=
∴AD=BD=2
∴∠BAD=∠ABD=45°
∵E是AB的中点,
∴BE=AE=AB=
延长BD至点,使得 D=BD=2,连接E,
则点P在E与AD的交点时,PE+PB的值最小,如下图,
理由如下:
∵ ’ ,D=BD=2,
∴ AD垂直平分B
∴AD上任意一点P,总有PB=P,
由“两点之间,线段最短”可知,点P在E与AD的交点处时,
PE+PB的值最小,最小值为E的长,此时过点E作EF⊥B于点F,如上图,
则∠EFB=∠EF=90°,
∵∠ABD=45°
∴EF=BF
∴EF2+BF2=BE2=2EF2
∴EF=BF==1
∴F=BD+D-BE=3
在Rt△EF中,由勾股定理得
E===
即的最小值为
故选:C
【点睛】本题考查了最短路径问题、勾股定理、等腰直角三角形等知识点,掌握最短路径的确定方法、灵活应用勾股定理是解题的关键.
3.A
【分析】过点C作CG⊥AB于点G,连接CE,根据,,,运用勾股定理的逆定理,证明△ABC是直角三角形,得到∠ACB=90°,根据平移性质证明四边形ADEC是平行四边形,得到CE∥AD,根据当DE⊥AB时, DE最小,此时,根据∠DEC=∠ECG=90°,证明四边形EDGC是矩形,得到DE=CG,运用面积法得到,求出,得到DE的最小值为.
【详解】过点C作CG⊥AB于点G,连接CE,
则∠AGC=90°,
∵中,,,,
∴,
∴是直角三角形,∠ACB=90°,
由平移知,AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
∴CE∥AD,
当DE⊥AB时, DE最小,
此时,∠DEC=∠ECG=90°,
∴四边形EDGC是矩形,
∴DE=CG,
∵
∴
∴,
∴,
∴DE的最小值为.
故选A.
【点睛】本题主要考查了勾股定理的逆定理,平移,平行四边形,三角形面积,垂线段,解决问题的关键是添加辅助线,熟练掌握用勾股定理的逆定理判断直角三角形,平移的性质,平行四边形的判定和性质,三角形面积公式,垂线段最短的性质.
4.D
【分析】点的运动轨迹以E为圆心,以AE的长为半径的圆,则当点落在DE上时,取最小值,根据折叠的性质利用勾股定理即可求解.
【详解】解:点的运动轨迹以E为圆心,以AE的长为半径的圆,则当点落在DE上时,取最小值,如图所示:
∵AB=4,E是AB边的中点,
∴AE=BE=2,
由沿所在直线折叠得到,
∴,
在平行四边形ABCD中,
∵∠B=60°,
∴∠BEG=∠AEH=30°,
∴BG=AH=1,
,
∴DH=AD=AH=6+1=7,
在Rt△DHE中,由勾股定理得:
,
∴,
∴的最小值是,
故选:D.
【点睛】本题考查了折叠的性质,平行四边形的性质,两点之间线段最短的综合应用,勾股定理,含30°角的直角三角形,确定点的位置,利用勾股定理解决问题是解题的关键.
5.B
【分析】由平行四边形的性质和直角三角形的性质可求FC,AN,EN,AE的长,即可求解.
【详解】解:如图,过点C作CF⊥AB于点F,过点N作NE⊥AD于E,
∵四边形ABCD是平行四边形,
∴,∠B=∠D=60°,
∵CF⊥AB,AN⊥CD,
∴,∠BCF=30°,
∴四边形AFCN是平行四边形,BFBC=2,CFBF=2,
∴AN=CF=2,
∵AN⊥CD,∠D=60°,
∴∠NAD=30°,
∴ENAN,AEEN=3,
∵AM⊥BC,NE⊥AD,
∴,
∴当MN⊥EN时,MN有最小值为3,
故选:B.
【点睛】本题考查了平行四边形的性质,直角三角形的性质,添加恰当辅助线构造直角三角形是解题的关键.
6.C
【分析】取BC的中点G,连接AG.首先证明∠BAC=90°,作点B关于AC的对称点F,连接GF,证FG⊥BC,则FG的长即为PB+PQ的最小值.
【详解】解:取BC的中点G,连接AG.在 ABCD中,AB=2,BC=4,∠D=60°,
∴AB=BG=2,∠ABG=∠D=60°,
∴△ABG是等边三角形,
∴AG=GC=2,∠AGB=∠BAG=60°,
∴∠GAC=∠GCA=30°,
∴∠BAC=90°,
作点B关于AC的对称点F,连接GF, 交AC于点P,由对称可知,B、A、F在一条直线上,AG=AF,
∵∠BAG=∠F+∠AGF=60°,
∴∠F=∠AGF=30°,
∴∠FGB=90°,
当点Q与点G重合时,PB+PQ=PF+PG=FG,FG的长即为PB+PQ的最小值,
∵∠F=∠AGF=30°,AG=GC=2,
∴BF=4,
,
∴BP+PQ的最小值为2.
故选:C.
【点睛】本题主要考查了轴对称﹣最短路线问题,勾股定理,等边三角形的性质,根据垂线段最短作出辅助线,确定点P,Q的位置是解答此题的关键.
7.B
【分析】取AB的中点G,接DG,CG,过C作于点H,根据三角形中位线的性质和勾股定理解答即可.
【详解】解:取AB得中点G,连接DG,CG,过点C作交AB延长线与H.
∵点D是AE的中点,点G是AB的中点,
∴AD = ED,AG=BG,
∴DG是的中位线,
∴DG=BE,
∵AB=BC=BE=2,
∴DG=1,BG=1,
∵,
∴,
∵,
∴,,
∴,
∴,
∴HG= BG +BH=2,
在中,
,
∵,
∴,
∴当且仅当D、G、C三点共线时,线段CD取最小值为.
故选:B.
【点睛】此题考查勾股定理,关解题的键是根据三角形的中位线定理和勾股定理解答.
8.C
【分析】根据平行四边形的性质可推出DE=2OD,则可得当OD⊥AC时,DO的值最小,即DE的值最小,过O作OF⊥AC于点F,利用等边三角形及直角三角形性质可求得AF=OA=,则可利用勾股定理求得OF的长,即可得出结论.
【详解】解:设AB与DE相交于点O,
∵四边形是平行四边形,是边长为2的等边三角形,
∴OA=OB=AB=1,OD=OE=DE.
即DE=2OD.
∴当OD⊥AC时,DO的值最小,即DE的值最小.
如图,过O作OF⊥AC于点F,
∴∠AFO =90°.
∵是等边三角形,
∴∠BAC =60°.
∴∠AOF =30°.
∴AF=OA=.
∴OF=.
当OD=OF时,DO的值最小,即DE的值最小,
∴DE=2OF=.
故选:C.
【点睛】此题考查了平行四边形、等边三角形及直角三角形的性质等知识,熟练掌握平行四边形的性质是解题的关键.
9.A
【分析】如图,把向上平移一个单位得:,作关于直线的对称点 连接,交直线于 连接,则此时四边形的周长最短,再利用勾股定理可得: ,利用从而可得答案.
【详解】解:如图,把向上平移一个单位得:,作关于直线的对称点 连接,交直线于 连接,
,
由
四边形是平行四边形,
所以此时:四边形的周长最短,
故选:
【点睛】本题考查的是图形与坐标,勾股定理的应用,轴对称的性质,平行四边形的判定与性质,掌握以上知识是解题的关键.
10.D
【分析】连接,取中点,连接,根据三角形任意两边之和大于第三边求最值即可.
【详解】解:连接,取中点,连接,
∵,
∴当取最大值时,三点共线,即在之间,
即,
∵分别是的中点,
∴,
∵,
∴,
∴,
∴,
故选:D.
【点睛】本题考查三角形的三边关系,中位线定理,平面直角坐标系中的点与几何,勾股定理,能够熟练掌握数形结合思想是解决本题的关键.
11.3
【分析】如图,过作交的延长线于点,根据平行四边形的性质,推出,从而得到,进而得到,根据,可知,当三点共线时,线段的和最小,利用所对的直角边是斜边的一半即可得解.
【详解】解:如图,过作交的延长线于点,
∵四边形为平行四边形,
∴,
∴,
∴,
∴,
∵,
∴当三点共线时,线段的和最小,
∵,,
∴,
即:的最小值等于3;
故答案为:3.
【点睛】本题考查平行四边形的性质,以及含的直角三角形.通过添加辅助线,构造含的直角三角形,利用垂线段最短进行求解,是解题的关键.本题是胡不归模型,平时多归纳总结,可以快速解题.
12.##
【分析】设点C坐标为(a,b),由平行四边形的性质可求b=,可得点C在直线y=上运动,再根据点C在y轴上时,AC的长度有最小值求解即可.
【详解】解:设点C坐标为(a,b),
∵顶点B、D分别在x轴和直线y= 3上,
∴点B,点D的纵坐标分别为0, 3,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴,
∴b=,
∴点C在直线y=上运动,
∴当点C在y轴上时,AC的长度有最小值,
∴对角线AC的最小值为:,
故答案为:.
【点睛】本题考查了平行四边形的性质,坐标与图形性质,确定点C的运动轨迹是本题的关键.
13.18
【分析】作点E关于AB的对称点G,连接EG交AB于点H,连接BG,FG,则EG⊥AB,GH=EH,BE=BG,可得当点G,B,F三点共线时,BG+BF最小,即为FG的长,此时周长的最小,再根据平行四边形的性质可得,GH=EH=6,进而得到EG=12,再由勾股定理,即可求解.
【详解】解:如图,作点E关于AB的对称点G,连接EG交AB于点H,连接BG,FG,则EG⊥AB,GH=EH,BE=BG,
∴周长为BE+BF+EF=BG+BF+EF,
∴当点G,B,F三点共线时,BG+BF最小,即为FG的长,此时周长的最小,
四边形是平行四边形,
,,
∴EG⊥CD,
,
∴,
∴GH=EH=6,
∴EG=12,
∴,
的最小值为,
的周长的最小值为,
故答案为:.
【点睛】本题考查轴对称最短问题,解题的关键是熟练掌握平行四边形的性质,勾股定理,属于中考常见题.
14. 平行四边形 ##
【分析】根据两组对边分别平行的四边形是平行四边形即可求解;当PQ是AQ和BC间距离时PQ取得最小值,计算四边形APCQ的周长即可.
【详解】解:如图,∵AQBC,CQAP,
∴四边形APCQ是平行四边形.
当PQ⊥BC时,PQ取得最小值,
∵四边形APCQ是平行四边形,
∴AH=HC=AC,QH=PH=PQ,
∵∠ABC=45°,AB=2,BC=,
∴AC=2,∠ACB=45°,
∵QP⊥BC,
∴∠PHC=45°,
∴PH=PC=,
∴PQ=,
∴QC=,
∴四边形APCQ的周长为:2PC+2QC=2×+2×=,
故答案为:平行四边形;.
【点睛】本题主要考查了平行四边形的性质,等腰三角形的判定,垂线段最短的性质,综合性较强.
15.
【分析】根据平行四边形的性质可得∠EBC=30°,过点Q作QM⊥BC于点M,过点P作PN⊥BC于点N,过点A作AH⊥BC于点H,根据含30°角的直角三角形的性质可得QM=BQ,PQ+BQ最小值即为PN的长,根据平行线之间的距离相等,可得PN=AH,根据勾股定理求出AH的长即可.
【详解】解:在平行四边形ABCD中,AD∥BC,AD=BC,
∴∠AEB=∠EBC,
∵AB=6,BC=8,DE=2,
∴AE=8-2=6,
∴AE=AB,
∴∠AEB=∠ABE,
∴∠ABE=∠EBC,
∵∠ABC=60°,
∴∠EBC=30°,
过点Q作QM⊥BC于点M,过点P作PN⊥BC于点N,过点A作AH⊥BC于点H,如图所示:
则QM=BQ,
∴PQ+BQ最小值即为PN的长,
∵AD∥BC,
∵PN=AH,
∵∠BAH=30°,AB=6,
∴BH=3,
根据勾股定理,可得AH=PN=,
∴PQ+BQ的最小值为,
故答案为:.
【点睛】本题考查了平行四边形的性质,直角三角形的性质,勾股定理等,通过构造直角三角形,找出PQ+BQ最小值即为PN的长是解题的关键.
16.
【分析】连接CD,根据三角形中位线的性质定理得出FG=,由勾股定理求出BC,再根据三角形等面积法求出CD,即可得出结果.
【详解】解:连接CD,
∵F、G分别是ED、EC的中点,
∴FG是△FDC的中位线,
∴FG=,
当CD最小时,FG最小,
当CD⊥AB时,CD最小,
在△ABC中,∠C=90°,AB=10,AC=8,
则BC=,
当CD⊥AB时,
,
∴,
解得:CD=,
∴FG的最小值为,
故答案为:.
【点睛】题目主要考查三角形中位线定理,勾股定理解三角形,垂线段最短,掌握三角形中位线定理是解题关键.
17.13
【分析】先由平移性质证明四边形为平行四边形,从而得,进而使得,再作关于直线的对称点,由对称性得,再由,求出,,由勾股定理求出即可.
【详解】解:连接,
由平移性质得:,,
四边形为平行四边形,
,
,
作关于直线的对称点,连接,,交延长线于,
由对称性得:,,,
,
,,
,
,,
,
,
,
的最小值为,
故答案为:
【点睛】本题主要考查了平行四边形的判定与性质、最短路径问题、勾股定理,解决此题的关键是证明四边形为平行四边形、再作关于直线的对称点,将的最小值转化为.
18.
【分析】过点A作AD//BC,且AD=MN,连接MD,则四边形ADMN是平行四边形,作点A关于BC的对称点A′,连接AA′交BC于点O,连接A′M,三点D、M、A′共线时,最小为A′D的长,利用勾股定理求A′D的长度即可解决问题.
【详解】解:过点A作AD//BC,且AD=MN,连接MD,
则四边形ADMN是平行四边形,
∴MD=AN,AD=MN,
作点A关于BC的对称点A′,连接A A′交BC于点O,连接A′M,
则AM=A′M,
∴AM+AN=A′M+DM,
∴三点D、M、A′共线时,A′M+DM最小为A′D的长,
∵AD//BC,AO⊥BC,
∴∠DA=90°,
∵,,,
∴BC=
BO=CO=AO=,
∴,
在Rt△AD中,由勾股定理得:
D=
∴的最小是值为:,
故答案为:
【点睛】本题主要考查了等腰三角形的性质,平行四边形的判定与性质,勾股定理等知识,构造平行四边形将AN转化为DM是解题的关键.
19.(1)
(2)
【分析】(1)过点作,交延长线于,根据平行四边形的性质得出,,根据含度角的直角三角形的性质得出,进而求得四边形的面积;
(2)连接,过点作于,交的延长线于点,根据轴对称的性质,以及两点直线线段最短可得到,当折线与线段重合时,线段的长度最短,根据勾股定理即可求解.
【详解】(1)解:过点作,交延长线于,
四边形是平行四边形,
,,,
,
,
四边形的面积;
故答案为:;
(2)连接,过点作于,交的延长线于点;
四边形为平行四边形,
,,
点为的中点,,
,,
,,
,
由勾股定理得:,
,
由翻折变换的性质得:,
,
,当折线与线段重合时,线段的长度最短,
此时,
故答案为:.
【点睛】本题考查了平行四边形的性质,含30度角的直角三角形的性质,勾股定理,轴对称求线段最值问题,掌握轴对称的性质是解题的关键.
20.(1)(4,2),4
(2)t的值是;
(3))S△EMD-S△OEN的值不会发生变化,S△EMD-S△OEN的值是3.
【分析】(1)作C(0,2)关于x轴的对称点C'(0,-2),连接DC'交x轴于N,此时CN+DN最小,最小值为C'D的长,由A(-1,0),B(3,0),四边形ABDC是平行四边形,可得DC=AB=4,D(4,2),在Rt△DCC'中,利用勾股定理求得DC'=4,即得CN+DN的最小值为4;
(2)根据S四边形OCDB=7,四边形OMDB的面积是8,知M在C的上方,且S△CDM=8-7=1,故CM DC=1,即(t-2)×4=1,可解得t的值;
(3)连接OD,由S△EMD-S△OEN=S△MOD+S△NOD=OM CD+ON OC=3,可得S△EMD-S△OEN的值是3,不会变化.
【详解】(1)解:作C(0,2)关于x轴的对称点C'(0,-2),连接DC'交x轴于N,此时CN+DN最小,最小值为C'D的长,如图:
∵A(-1,0),B(3,0),
∴AB=4,
∵四边形ABDC是平行四边形,
∴DC=AB=4,
∴D(4,2),
在Rt△DCC'中,
DC'=,
∴CN+DN的最小值为4,
故答案为:(4,2),4;
(2)解:如图:
∵S四边形OCDB=×(4+3)×2=7,
又四边形OMDB的面积是8,
∴M在C的上方,且S△CDM=8-7=1,
∴CM DC=1,
即(t-2)×4=1,
解得t=,
答:t的值是;
(3)解:S△EMD-S△OEN的值不会发生变化,理由如下:
连接OD,如图:
∵S△EMD-S△OEN=S四边形MOND,
∴S△EMD-S△OEN
=S△MOD+S△NOD
=OM CD+ON OC
=t×4+(3-2t)×2
=2t+3-2t
=3,
∴S△EMD-S△OEN的值是3,不会变化.
【点睛】本题考查四边形综合应用,涉及平移的性质、轴对称的性质,坐标与图形性质、平行四边形的性质、三角形面积等知识;熟练掌握平移的性质是解题的关键.
21.(1)见解析;
(2)①EC=OA,证明见解析;②.
【分析】(1)证明∠AFE+∠AFB=180°,可得结论;
(2)①结论:EC=AO.连接EO,OC,证明△EOC是等腰直角三角形,可得结论;
②如图2中,取AE的中点J,连接OJ.证明OJ∥EB,推出OF⊥OJ时,OF的值最小,此时四边形OFEJ是矩形,利用勾股定理求出OA,可得结论.
【详解】(1)证明:∵∠AEF=90°,AE=EF,
∴∠EAF=∠EFA=45°,
∵2∠CBF+∠EAF=135°,
∴∠CBF=45°,
∵∠C=90°,
∴∠CFB=90°-45°=45°,
∴∠CFB=∠AFE,
∵∠CFB+∠AFB=180°,
∴∠AFE+∠AFB=180°,
∴E、F、B共线.
(2)解:①结论:EC=OA.
理由:如图1中,连接EO,CO.
∵∠AEB=∠ACB=90°,OA=OB,
∴OE=OA=OB=OC,
∴∠OAC=∠OCA,∠OEB=∠OBE,
∵∠BOC=∠OAC+∠OCA=2∠OCA,∠AOE=∠OEB+∠OBE=2∠OBE,
∴∠BOC+∠AOE=2∠CAO+2∠OBE=2(∠OAC+∠OBE)=2∠CFB=90°,
∴∠EOC=90°,
∴△EOC是等腰直角三角形,
∴EC=EO=OA;
②如图2中,取AE的中点J,连接OJ.
∵AJ=EJ,AO=OB,
∴OJ∥EB,
∴OF⊥OJ时,OF的值最小,此时四边形OFEJ是矩形,
∴EF=AE=OJ=2,AJ=EJ=1,
∴,
∴EC=OA=.
【点睛】本题属于三角形综合题,考查了等腰直角三角形的性质和判定,勾股定理,三角形中位线定理,垂线段最短等知识,解题的关键是学会添加常用辅助线,构造等腰直角三角形解决问题.
22.(1)6,4,(9,4)
(2)存在,
(3),证明见解析
【分析】(1)根据二次根式有意义的条件和绝对值的意义求解即可;
(2)连接CE,根据中位线定理可知MN=CE,当时,CE有最小值,根据三角形面积可求CE的值,即可求解;
(3)连接QF,可证△OCP≌△FCQ,得OP=QF,在直角三角形QFP中,,可求解.
【详解】(1)解:∵,,,
∴,
∴6-a=0,b-4=0,
∴a=6,b=4.
∴点B的坐标为(9,4).
故答案为:6,4,(9,4).
(2)解:MN存在最小值,理由是:
连接CE,如图1,
∵M、N分别是CD、DE的中点,
∴MN=CE.
当时,CE有最小值,
∵C(3,4),A(6,0),
∴OA=6,AB=OC=5,
∴,
∴MN=.
(3)解:连接QF,如图2,
由旋转可知,OC=OF,∠OCF=90°,∠O=∠CFO=45°.
∵△CPQ为等腰直角三角形CPQ,
∴CP=CQ,∠PCQ=90°,∠QCP=45°,
∴∠OCF=∠PCQ,
∴∠OCF-∠PCF=∠PCQ-∠PCF,
即∠OCP=∠FCQ,
在△OCP和△FCQ中,
∴△OCP≌△FCQ(SAS),
∴OP=QF,
∠QFP=∠QFC+∠CFO=45°+45°=90°,
∴,
∵OP=QF,
∴
【点睛】本题考查了全等三角形的判定与性质、三角形的中位线、勾股定理等知识,熟练掌握这些知识是解题的关键.
23.(1)85
(2)5+5
(3)2+2
【分析】(1)根据平角的定义,翻折的性质求解即可;
(2)作BH⊥AD于H.勾股定理解Rt△ABH,由四边形ABCD是平行四边形,AD∥BC,可得∠APA′=90°,PH=BH,根据PA=AH+PH 即可求解;
(3)作BH⊥AD于H,连接BP.勾股定理求得PB,当BA′的长度最小时,△BFA′的周长最小,由BA′≥PB﹣PA′,求得,然后即可求得△BFA′的周长的最小值.
【详解】(1)如图1中,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:∠A′PB=∠APB=×170°=85°.
故答案为85.
(2)如图2中,作BH⊥AD于H.
在Rt△ABH中,∵∠AHB=90°,AB=10,∠A=60°,
∴AH=5,BH=5,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∴PH=BH=5,
∴PA=AH+PH=5+5.
(3)如图3中,作BH⊥AD于H,连接BP.
∵PA=8,AH=5,
∴PH=8﹣5=3,
∵BH=5,
∴PB===2,
由翻折可知:PA=PA′=8,FA=FA′,
∴△BFA′的周长=FA′+BF+BA′=AF+BF+BA′=AB+BA′=10+BA′,
∴当BA′的长度最小时,△BFA′的周长最小,
∵BA′≥PB﹣PA′,
∴BA′≥2﹣8,
∴BA′的最小值为2﹣8,
∴△BFA′的周长的最小值为10+2﹣8=2+2.
【点睛】本题考查了勾股定理解直角三角形,平行四边形的性质,折叠的性质,轴对称求线段和最值问题,综合运用以上知识是解题的关键.
24.(1)见解析;(2)四边形ABPE是平行四边形,理由见解析,BP =5cm;(3),
【分析】(1)证明△AEO△CPO即可说明PO=OE;
(2)证明EP∥AB,即可证明四边形ABPE是平行四边形,利用三角形中位线定理即可求解;
(3)求得四边形ABPE的周长为:6+10+PE=16+PE,得到当PE⊥BC时,PE最小,利用平行四边形的面积公式求得PE,即可求得四边形ABPE的周长最小值,根据△AEO△CPO以及勾股定理即可求得BP的长度.
【详解】(1)证明:∵四边形ABCD是平行四边形,点O为AC的中点,
∴AE∥PC,AO=OC,
∴∠EAO=∠PCO,∠AOE=∠COP,
∴△AEO△CPO,
∴PO=OE;
(2)∵CA⊥AB,且PO⊥AC,
∴PO∥AB,即EP∥AB,
∵四边形ABCD是平行四边形,
∴AE∥BP,
∵CA⊥AB,且AB=6cm,AC=8cm,
∴BC=(cm),
∴四边形ABPE是平行四边形,
∵点O为AC的中点,且PO∥AB,
∴BP=PC=BC=5(cm);
(3)四边形ABPE的周长为:AB+BP+PE+AE,
由(1)知△AEO△CPO,则AE=CP,
∴BP+AE=BP+CP=BC=10,
∴四边形ABPE的周长为:6+10+PE=16+PE,
则PE最小时,四边形ABPE的周长最小,
∴当PE⊥BC时,PE最小(垂线段最短),
∵BCPE=ABAC,
∴PE=(cm),
∴四边形ABPE的周长最小值为16+=(cm),
∵△AEO△CPO,
∴PO=EO=PE=(cm),OC=AC=(cm),
∴PC=(cm),
∴BP=BC-PC=(cm),
故答案为:,.
.
【点睛】本题考查了平行四边形的判定和性质,三角形中位线定理,全等三角形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题.
答案第1页,共2页
答案第1页,共2页
