专题18.11三角形的中位线 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.11三角形的中位线 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 810.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 21:55:19 | ||
图片预览


文档简介
专题18.11 三角形的中位线(巩固篇)(专项练习)
一、单选题
1.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为( )
A.32 B.16 C.8 D.4
2.如图,在ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
3.下列命题是假命题的是( )
A.任意一个三角形中,三角形两边的差小于第三边
B.三角形的中位线平行于三角形的第三边,并且等于第三边的一半
C.如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等
D.一组对边平行且相等的四边形是平行四边形
4.如图,ABC中,AB=AC=12,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则CDE的周长为( )
A.11 B.17 C.18 D.16
5.如图,四边形ABCD四边的中点分别为E,F,G,H,对角线AC与BD相交于点O,若四边形EFGH的周长是3,则AC+BD的长为( )
A.3 B.6 C.9 D.12
6.如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD,下列结论错误的是( )
A.AD=CD B.∠A=∠DCE C.∠ADE=∠DCB D.∠A=2∠DCB
7.如图,在中,是的中点,在上,且,连接,交于点,若,则( )
A.15 B.18 C.20 D.25
8.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△AnBnCn的周长为( )
A.a B.a C.a D.a
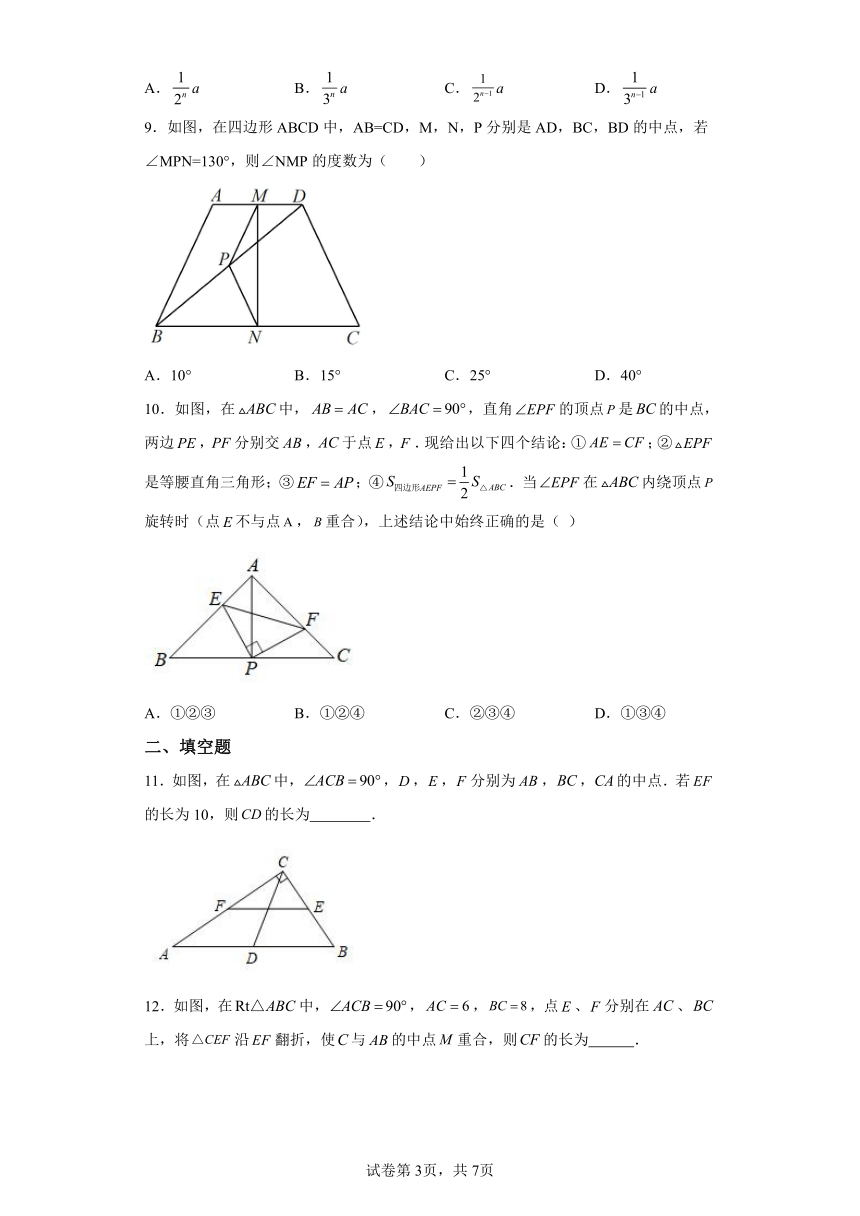
9.如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )
A.10° B.15° C.25° D.40°
10.如图,在中,,,直角的顶点是的中点,两边,分别交,于点,.现给出以下四个结论:①;②是等腰直角三角形;③;④.当在内绕顶点旋转时(点不与点,重合),上述结论中始终正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
11.如图,在中,,,,分别为,,的中点.若的长为10,则的长为 .
12.如图,在中,,,,点、分别在、上,将沿翻折,使与的中点重合,则的长为 .
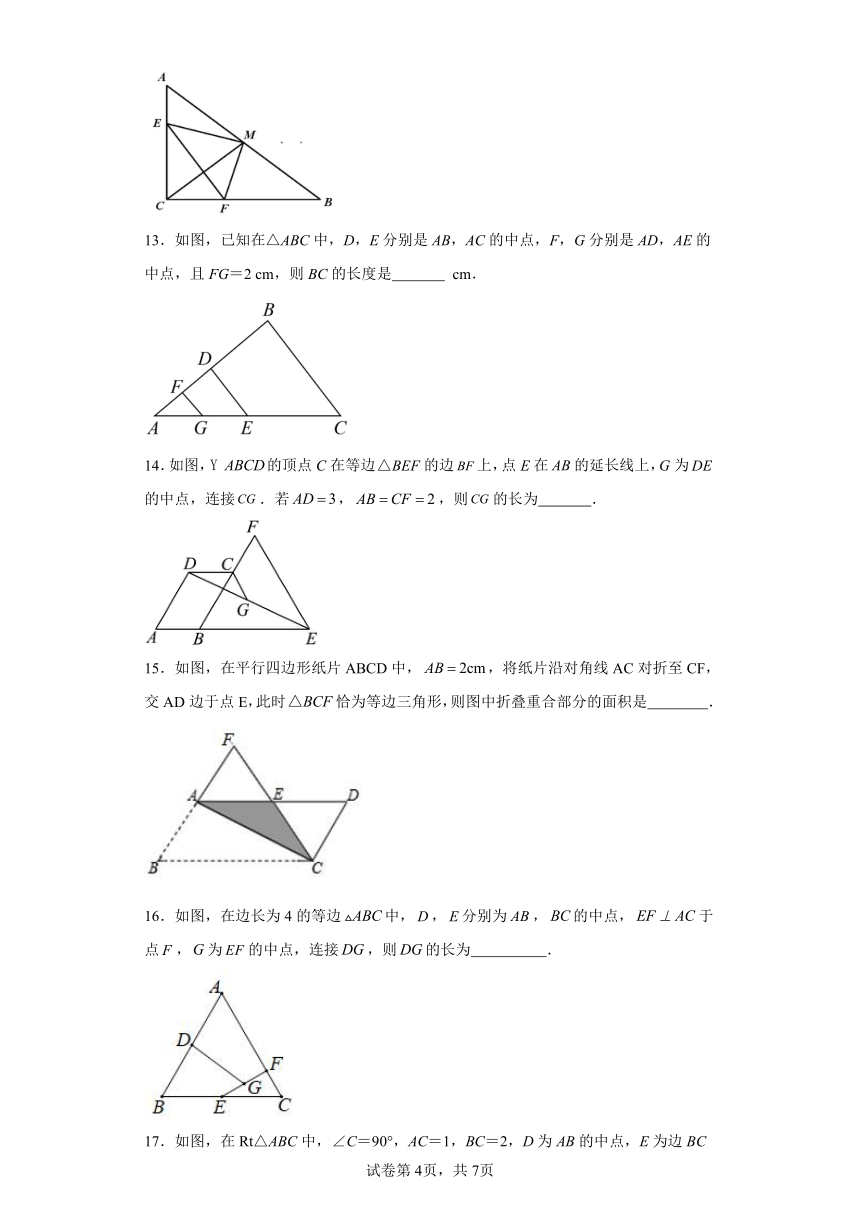
13.如图,已知在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2 cm,则BC的长度是 cm.
14.如图,的顶点C在等边的边上,点E在的延长线上,G为的中点,连接.若,,则的长为 .
15.如图,在平行四边形纸片ABCD中,,将纸片沿对角线AC对折至CF,交AD边于点E,此时恰为等边三角形,则图中折叠重合部分的面积是 .
16.如图,在边长为4的等边中,,分别为,的中点,于点,为的中点,连接,则的长为 .
17.如图,在Rt△ABC中,∠C=90°,AC=1,BC=2,D为AB的中点,E为边BC上一点,将△ADE沿DE翻折得到△A'DE,A'D与BC交于F.若△A'DE与△BDE重叠部分的面积占△ABE面积的,则BF的长为 .
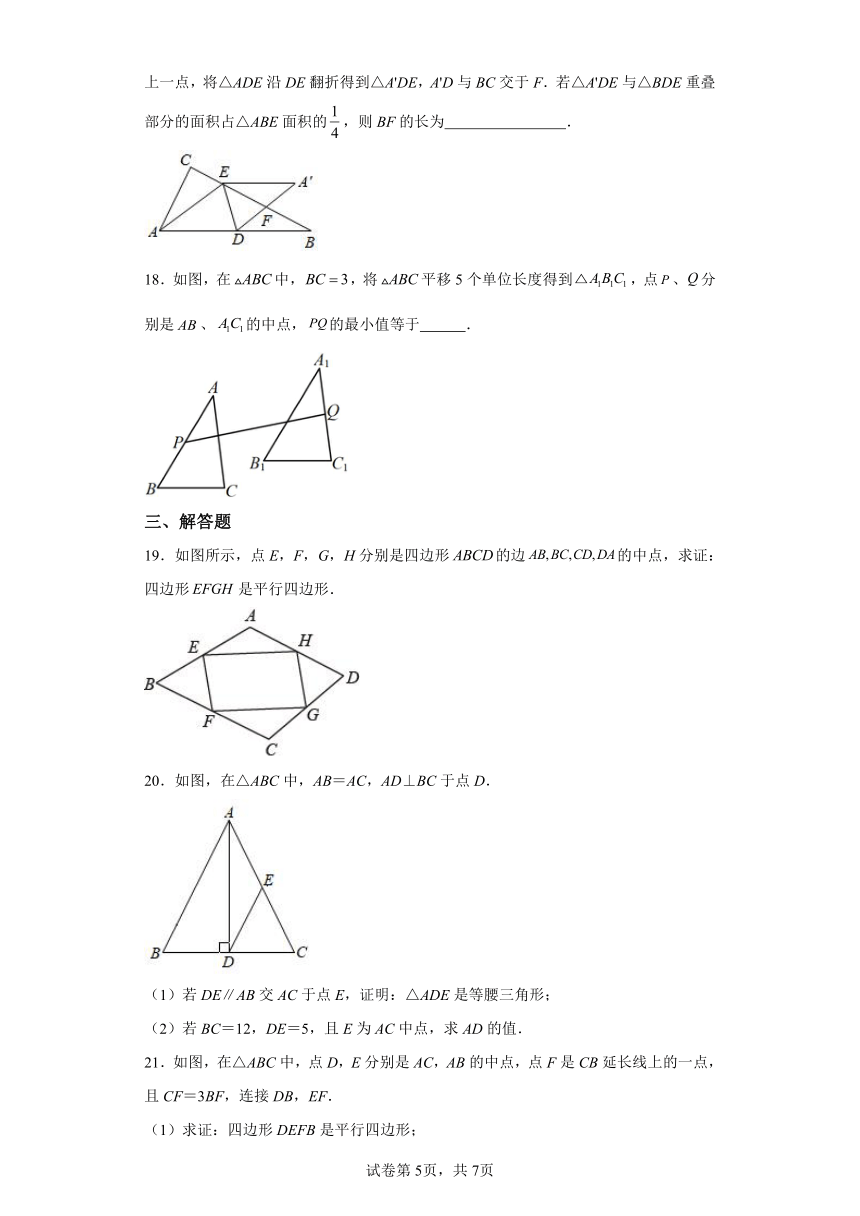
18.如图,在中,,将平移5个单位长度得到,点、分别是、的中点,的最小值等于 .
三、解答题
19.如图所示,点E,F,G,H分别是四边形的边的中点,求证:四边形是平行四边形.
20.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若DE∥AB交AC于点E,证明:△ADE是等腰三角形;
(2)若BC=12,DE=5,且E为AC中点,求AD的值.
21.如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12cm,DE=4cm,求四边形DEFB的周长.
22.在Rt△ABC中,∠BAC=90°,E,F分别是AB,AC上的点,且EF∥BC,作EG平分∠AEF交AC于点G,在EF上取点D,使ED=EA,连接DG并延长,交BA的延长于点P,连接PF.
(1)求证:PD⊥EF;
(2)若ED=DF,求∠B的大小.
(3)在(2)的条件下,若四边形AEDG的面积为S,请直接写出△PEF的面积(用含S的式子表示).
23.如图,直线与轴相交于点,直线经过点,与轴交于点,与轴交于点,与直线相交于点.
求直线的函数关系式;
点是上的一点,若的面积等于的面积的倍,求点的坐标.
设点 的坐标为,是否存在 的值使得 最小?若存在,请求出点 的坐标;若不存在,请说明理由.
24.(1)探究:如图(1),点P在线段AB上,在AB的同侧作△APC和△BPD,满足PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G分别是AC、BD、CD边中点,连接EF、FG、EG.求证:∠EFG=∠GEF.
(2)应用:如图(2),点P在线段AB上方,∠APC=∠BPD=90°,图(1)题中的其他条件不变,若EF=2,则四边形ABDC的面积为 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据等腰三角形的性质和中位线的性质求解即可.
【详解】∵AD=AC,
∴是等腰三角形,
∵AE⊥CD,
∴,
∴E是CD的中点,
∵F是BC的中点,
∴EF是△BCD的中位线,
∴,
故答案为:C.
【点睛】本题考查了三角形的线段长问题,掌握等腰三角形的性质和中位线的性质是解题的关键.
2.B
【分析】根据直角三角形的斜边的中线等于斜边的一半,得到DF=5,由三角形中位线的性质得到DE=8,最后由线段的和差解题即可.
【详解】解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=5,
∵BC= 16,D、E分别是AB,AC的中点,
∴DE=BC=8,
∴EF=DE-DF=3,
故选:B.
【点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.
3.C
【分析】根据三角形两边之差小于第三边、中位线定理、平行四边形的判定方法依次即可求解.
【详解】解:选项A:三角形的两边之差小于第三边,故选项A正确,不符合题意;
选项B:三角形的中位线平行且等于第三边的一半,故选项B正确,不符合题意;
选项C:一个角的两边分别平行另一个角的两边,则这两个角相等或互补,故选项C不正确,是假命题,符合题意;
选项D:一组对边平行且相等的四边形是平行四边形,故选项D正确,不符合题意;
故选:C.
【点睛】本题考查了三角形中位线定理,三角形三边之间的关系,平行四边形的判定等知识点,熟练掌握各个基本定理和性质是解决本类题的关键.
4.B
【分析】根据等腰三角形的性质得到BD=DC,根据三角形中位线定理求出DE,根据三角形的周长公式计算,得到答案.
【详解】解:∵AB=AC,AD平分∠BAC,
∴,
∵点E为AC的中点,
∴,
∴△CDE的周长=CD+CE+DE=17,
故选:B.
【点睛】本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
5.A
【分析】先由三角形的中位线定理推知四边形EFGH是平行四边形,然后求解即可.
【详解】解:如图,
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知:
EF∥AC,GH∥AC且EF=GH=AC,EH=FG=BD,
∴四边形EFGH是平行四边形,
∵四边形EFGH的周长是3,即EF+GH+EH+FG=3,
∴AC+BD=3,
故选:A.
【点睛】本题主要考查中点四边形,解题时,利用三角形中位线定理判定四边形EFGH是平行四边形是解题的关键.
6.D
【分析】根据题意可知DE是AC的垂直平分线,由此即可一一判断.
【详解】∵DE是AC的垂直平分线,
∴DA=DC,AE=EC,故A正确,
∴DE∥BC,∠A=∠DCE,故B正确,
∴∠ADE=∠CDE=∠DCB,故C正确,
故选D.
【点睛】本题考查作图-基本作图、线段的垂直平分线的性质、等腰三角形的性质,三角形中位线定理等知识,解题的关键是熟练运用这些知识解决问题.
7.D
【分析】过D作DG∥AB,交CE于G,连接DE,根据三角形中位线的定理可得CG=EG,通过△DGF △AEF,可得AF=DF,再利用三角形的面积可求解.
【详解】过D作DG∥AB,交CE于G,连接DE,
∵D为BC的中点,
∴DG为△BCE的中位线,
∴BE=2GD,CG=EG,
∵,
∴AE=GD,
∵DG∥AB,
∴∠AEF=∠DGF,∠EAF=∠GDF,
∴△DGF △AEF,
∴AF=DF,
∵,
∴S△ABD=30,S△AED=10,
∴S△AEF=5,
∴S四边形DCEF=S△ABD S△AEF=30 5=25,
故选:D.
【点睛】本题主要考查三角形的面积,全等三角形的判定与性质,三角形的中位线,添加辅助线,构造全等三角形,是解题的关键.
8.A
【分析】根据三角形中位线的性质可知的周长的周长,的周长的周长,以此类推找出规律,写出代数式,再整理即可选择.
【详解】解:∵以△ABC的各边的中点为顶点作,
∴的周长的周长.
∵以各边的中点为顶点作,
∴的周长的周长,
…,
∴的周长
故选:A.
【点睛】本题主要考查三角形中位线的性质,根据三角形中位线的性质求出前2个三角形的面积总结出规律是解答本题的关键.
9.C
【详解】分析:根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和三角形内角和定理即可求出∠PMN的度数.
详解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN,∴△PMN是等腰三角形.
∵∠MPN=130°,∴∠PMN==25°.
故选C.
点睛:本题考查了三角形中位线定理及等腰三角形的判定和性质,解题时要善于根据已知信息,确定应用的知识.
10.B
【分析】根据等腰直角三角形的性质得出∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,求出∠APE=∠CPF,证△APE≌△CPF,推出AE=CF,EP=PF,推出S△AEP=S△CPF,求出S四边形AEPF=S△APC=S△ABC,EF不是△ABC的中位线,故EF≠AP,即可得出答案.
【详解】解:∵△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,
∴∠EPF-∠APF=∠APC-∠APF,
∴∠APE=∠CPF,
在△APE和△CPF中
,
∴△APE≌△CPF(ASA),
∴AE=CF,EP=PF,
∴△EPF是等腰直角三角形,
∴①正确;②正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故③错误;
∵△APE≌△CPF,
∴S△AEP=S△CPF,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=S△APC=S△ABC,
∴④正确;
∴正确的有①②④,
故选:B.
【点睛】本题考查了等腰三角形性质,三角形中位线的性质,三角形三边关系定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.
11.10
【分析】根据三角形中位线定理求出AB,根据直角三角形的性质解答.
【详解】解:∵E、F分别为BC、AC的中点,
∴AB=2EF=20,
∵∠ACB=90°,点D为AB的中点,
∴,
故答案为:10.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
12.
【分析】过点M作于N,则,可得MN是的中位线,利用三角形中位线定理可得MN=AC=3,BN=CN=BC=4,设CF=x,则NF=4-x,由折叠的性质可得MF=CF,在中,利用勾股定理即可求解.
【详解】解:过点M作于N,
∵,,
∴,
∵是的中点,
∴MN是的中位线,
∴MN=AC=3,BN=CN=BC=4,
设CF=x,则NF=4-x,
∵将沿翻折,使与的中点重合,
∴MF=CF=x,
在中,,
∴,解得,
∴CF=.
故答案为:.
【点睛】本题考查折叠的性质,三角形的中位线定理,勾股定理等知识,熟练掌握三角形的中位线定理,利用勾股定理建立方程求解是解题的关键.
13.8
【解析】略
14.
【分析】延长DC交EF于点M(图见详解),根据平行四边形与等边三角形的性质,可证△CFM是等边三角形,BF=BE=EF=BC+CF=5,可求出CF=CM=MF=2,可得C、G是DM和DE的中点,根据中位线的性质,可得出CG=,代入数值即可得出答案.
【详解】解:如下图所示,延长DC交EF于点M,,,
平行四边形的顶点C在等边的边上,
,
是等边三角形,
.
在平行四边形中,,,
又是等边三角形,
,
.
G为的中点,,
是的中点,且是的中位线,
.
故答案为:.
【点睛】本题考查了平行四边形的性质、等边三角形的性质、中位线等知识点,延长DC交EF于点M,利用平行四边形、等边三角形性质求出相应的线段长,证出是的中位线是解题的关键.
15.
【分析】为等边三角形,点A为BF的中点,可得,求得,再证明出点E为AD的中点,得到,可求出面积.
【详解】解:折叠至处,
AB=AF=2cm,BC=BF=CF=4cm,
为等边三角形,
,,
又四边形ABCD为平行四边形,
,
,
cm,CD=AB=2cm,
=,
点A为BF的中点,,
AE为的中位线,
,
点E为AD的中点,
==为折叠重合部分的面积,
故答案为:.
【点睛】本题考查了折叠问题以及等边三角形和平行四边形的综合问题,还涉及勾股定理,需要有一定的推理论证能力,熟练掌握等边三角形和平行四边形的性质是解题的关键.
16.
【分析】连接DE,根据题意可得ΔDEG是直角三角形,然后根据勾股定理即可求解DG的长.
【详解】解:连接DE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=AC.
∵ΔABC是等边三角形,且BC=4,
∴∠DEB=60°,DE=2.
∵EF⊥AC,∠C=60°,EC=2,
∴∠FEC=30°,EF=.
∴∠DEG=180°-60°-30°=90°.
∵G是EF的中点,
∴EG=.
在RtΔDEG中,DG=.
故答案为.
【点睛】本题主要考查了等边三角形的性质,勾股定理以及三角形中位线性质定理,记住和熟练运用性质是解题的关键.
17.##
【分析】依据勾股定理可得AB的长,由△DEF与△ABE面积关系推出F为BE中点,再根据三角形中位线定理以及勾股定理即可得出CE的长,进而得到BF的长.
【详解】解:如图,
Rt△ABC中,∠C=90°,AC=1,BC=2,
∴,
∵点D是AB的中点,
∴S△BDE=S△ABE,
又∵△DEF的面积占△ABE面积的,
∴S△FDE=S△ABE=S△DBE,
∴F是BE的中点,
又∵D是AB的中点,
∴DF是△ABE的中位线,
∴DF∥AE,
∴∠2=∠3,
又∵∠2=∠1,
∴∠1=∠3,
∴AE=AD=AB=,
Rt△ACE中,,
∴BE=2﹣=,
∴BF=BE=,
故答案为:.
【点睛】本题考查勾股定理、三角形中位线定理、折叠图形的特征等知识点,将题目中三角形面积关系转化为线段间的关系是解题关键.
18.
【分析】取A1B1的中点P′,连接QP′、PP′,如图,根据平移的性质得到PP′=7,B1C1=BC=4,再利用P′Q为△A1B1C1的中位线得到P′Q=2,利用三角形三边的关系得到PP′﹣P′Q≤PQ≤PP′+P′Q(当且仅当P、P′、Q三点共线时取等号),从而得到PQ的最小值.
【详解】解:取A1B1的中点P′,连接QP′、PP′,如图:
∵△ABC平移5个单位长度得到△A1B1C1,
∴PP′=5,B1C1=BC=3,
∵Q是A1C1的中点,P′为A1B1的中点,
∴P′Q为△A1B1C1的中位线,
∴P′Q=B1C1=,
∴PP′﹣P′Q≤PQ≤PP′+P′Q(当且仅当P、P′、Q三点共线时取等号),
即,,
∴PQ的最小值为.
故答案为
【点睛】本题主要考查平移的性质和三角形三边关系,三角形的中位线的性质,掌握三角形三边关系是解题的关键.
19.见解析
【分析】连接BD,利用三角形的中位线定理证明得出,从而得到四边形是平行四边形
【详解】解:如图,连接.
∵点E,H分别是线段的中点,
∴是的中位线,
∴EH∥BD,.
同理,.
∴,
∴四边形是平行四边形.
【点睛】此题主要考查了三角形中位线定理和平行四边形的判定方法,题目比较典型,又有综合性,难度不大,解题的关键是正确的添加辅助线,把四边形的问题转化为三角形的问题.
20.(1)见解析;(2)8
【分析】(1)根据“三线合一”性质先推出∠BAD=∠CAD,再结合平行线的性质推出∠BAD=∠ADE,从而得到∠ADE=∠EAD,即可根据“等角对等边”证明;
(2)根据题意结合中位线定理可先推出AC=2DE,然后在Rt△ADC中利用勾股定理求解即可.
【详解】(1)证:∵在△ABC中,AB=AC,
∴△ABC为等腰三角形,
∵AD⊥BC于点D,
∴由“三线合一”知:∠BAD=∠CAD,
∵DE∥AB交AC于点E,
∴∠BAD=∠ADE,
∴∠CAD=∠ADE,
即:∠ADE=∠EAD,
∴AE=DE,
∴△ADE是等腰三角形;
(2)解:由“三线合一”知:BD=CD,
∵BC=12,
∴DC=6,
∵E为AC中点,
∴DE为△ABC的中位线,
∴AB=2DE,
∴AC=AB=2DE=10,
在Rt△ADC中,,
∴AD=8.
【点睛】本题考查等腰三角形的性质与判定,勾股定理解三角形,以及三角形的中位线定理等,掌握等腰三角形的基本性质,熟练运用中位线定理和勾股定理计算是解题关键.
21.(1)见解析;(2)平行四边形DEFB的周长=
【分析】(1)证DE是△ABC的中位线,得DE∥BC,BC=2DE,再证DE=BF,即可得出四边形DEFB是平行四边形;
(2)由(1)得:BC=2DE=8(cm),BF=DE=4cm,四边形DEFB是平行四边形,得BD=EF,再由勾股定理求出BD=10(cm),即可求解.
【详解】(1)证明:∵点D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE//BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
∴四边形DEFB是平行四边形;
(2)解:由(1)得:BC=2DE=8(cm),BF=DE=4cm,四边形DEFB是平行四边形,
∴BD=EF,
∵D是AC的中点,AC=12cm,
∴CD=AC=6(cm),
∵∠ACB=90°,
∴BD==10(cm),
∴平行四边形DEFB的周长=2(DE+BD)=2(4+10)=28(cm).
【点睛】本题考查了平行四边形的判定与性质、三角形中位线定理、勾股定理等知识;熟练掌握三角形中位线定理,证明四边形DEFB为平行四边形是解题的关键.
22.(1)详见解析;(2)60°;(3)S△PEF=3S.
【分析】(1)由“SAS”可证△AEG≌△DEG,可得∠GAE=∠GDE=90°,可得PD⊥EF;
(2)由线段垂直平分线的性质可得EG=GF,可得∠GFE=∠GEF,由直角三角形的性质可求∠AEG=∠GEF=∠GFE=30°,由平行线的性质可求解;
(3)先证△PEF是等边三角形,可证四边形AEDG的面积=S△AEF=S△PEF,即可求解.
【详解】(1)∵EG平分∠AEF,
∴∠AEG=∠DEG,
在△AEG和△DEG中,
,
∴△AEG≌△DEG(SAS)
∴∠GAE=∠GDE=90°,
∴PD⊥EF;
(2)∵ED=DF,PD⊥EF,
∴EG=GF,
∴∠GFE=∠GEF,
∴∠AEG=∠GEF=∠GFE,
∵∠AEG+∠GEF+∠GFE=90°,
∴∠AEG=∠GEF=∠GFE=30°,
∴∠AEF=60°,
∵EF∥BC,
∴∠AEF=∠B=60°
(2)∵ED=DF,PD⊥EF,
∴PE=PF,且∠PEF=60°,
∴△PEF是等边三角形,
∵AF⊥AB,
∴AE=AP,
∴S△AEF=S△AFP,
∵∠BAC=90°,∠AEG=30°,
∴EG=2AG,
∴GF=2AG,
∴2S△AEG=S△EGF,
∵ED=DF,
∴S△GED=S△GFD,
∴S△GED=S△GFD=S△AEG,
∴四边形AEDG的面积=S△AEF=S△PEF,
∴S△PEF=3S.
【点睛】本题考查了三角形的综合问题,掌握全等三角形的性质以及判定定理、线段垂直平分线的性质、直角三角形的性质、平行线的性质是解题的关键.
23.(1)y=x-2;(2)( ,)或(, );(3)(,3).
【分析】(1)把点(3,-1),点B(6,0)代入直线l2,求出k、b的值即可;
(2)设点P的坐标为(t, t-2),求出D点坐标,再由S△ABP=2S△ABD求出t的值即可;
(3)作直线y=3,作点A关于直线y=3的对称点A′,连结A′B,利用待定系数法求出其解析式,根据点Q(m,3)在直线A′B上求出m的值,进而可得出结论.
【详解】解:(1)由题知:
解得:
,
故直线l2的函数关系式为:y=x-2;
(2)由题及(1)可设点P的坐标为(t, t-2).
解方程组 ,得 ,
∴点D的坐标为(,-).
∵S△ABP=2S△ABD,
∴AB |t-2|=2×AB |-|,即|t-2|=,解得:t=或t=,
∴点P的坐标为( ,)或(, );
(3)作直线y=3(如图),再作点A关于直线y=3的对称点A′,连结A′B.
由几何知识可知:A′B与直线y=3的交点即为QA+QB最小时的点Q.
∵点A(3,0),
∴A′(3,6)
∵点B(6,0),
∴直线A′B的函数表达式为y=-2x+12.
∵点Q(m,3)在直线A′B上,
∴3=-2m+12
解得:m=,
故存在m的值使得QA+QB最小,此时点Q的坐标为(,3).
【点睛】此题考查一次函数综合题,涉及到一次函数图象上点的坐标特点,轴对称最短路线问题,三角形的面积公式,解题关键在于在解答(3)时要注意作出辅助线,利用轴对称的性质求解.
24.(1)见解析;(2)4
【分析】(1)连接AD,BC,可证得△APD≌△CPB,从而得到AD=CB.再由三角形中位线定理,可得EG=GF,即可求证;
(2)连接AD、BC交于点M,BC、PD交于点N,可证得△APD≌△CPB,从而得到AD=CB.∠ADP=∠CBP,再由∠CND=∠PNB,AD⊥BC,再由三角形中位线定理,可得△GEF为等腰直角三角形,从而得到,再由,即可求解.
【详解】证明:(1) 如图,连接AD,BC,
∵∠APC=∠BPD,
∴∠APD=∠CPB.
∵PA=PC,PD=PB,
∴△APD≌△CPB,
∴AD=CB.
∵E、G、F分别为AC、CD、DB的中点,
∴EG=AD,GF=BC,
∴EG=GF,
∴∠GEF=∠GFE.
(2)如图,连接AD、BC交于点M,BC、PD交于点N,
∵∠APC=∠BPD=90°,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB,
∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS),
∴AD=CB,∠ADP=∠CBP,
∵∠CND=∠PNB,
∴∠DMN=∠BPD=90°,
∴AD⊥BC,
∵E、G、F分别为AC、CD、DB的中点,
∴EG是△ACD的中位线,GF是△DCB的中位线,
∴EG=AD,GF=BC, EGAD,GFBC,
∴GE=GF,GE⊥GF,
∴△GEF为等腰直角三角形,
∴,
∵EF=2,
∴,
∴.
故答案为:4
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法、等腰直角三角形的性质及三角形中位线的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为( )
A.32 B.16 C.8 D.4
2.如图,在ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
3.下列命题是假命题的是( )
A.任意一个三角形中,三角形两边的差小于第三边
B.三角形的中位线平行于三角形的第三边,并且等于第三边的一半
C.如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等
D.一组对边平行且相等的四边形是平行四边形
4.如图,ABC中,AB=AC=12,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则CDE的周长为( )
A.11 B.17 C.18 D.16
5.如图,四边形ABCD四边的中点分别为E,F,G,H,对角线AC与BD相交于点O,若四边形EFGH的周长是3,则AC+BD的长为( )
A.3 B.6 C.9 D.12
6.如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD,下列结论错误的是( )
A.AD=CD B.∠A=∠DCE C.∠ADE=∠DCB D.∠A=2∠DCB
7.如图,在中,是的中点,在上,且,连接,交于点,若,则( )
A.15 B.18 C.20 D.25
8.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△AnBnCn的周长为( )
A.a B.a C.a D.a
9.如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )
A.10° B.15° C.25° D.40°
10.如图,在中,,,直角的顶点是的中点,两边,分别交,于点,.现给出以下四个结论:①;②是等腰直角三角形;③;④.当在内绕顶点旋转时(点不与点,重合),上述结论中始终正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
11.如图,在中,,,,分别为,,的中点.若的长为10,则的长为 .
12.如图,在中,,,,点、分别在、上,将沿翻折,使与的中点重合,则的长为 .
13.如图,已知在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2 cm,则BC的长度是 cm.
14.如图,的顶点C在等边的边上,点E在的延长线上,G为的中点,连接.若,,则的长为 .
15.如图,在平行四边形纸片ABCD中,,将纸片沿对角线AC对折至CF,交AD边于点E,此时恰为等边三角形,则图中折叠重合部分的面积是 .
16.如图,在边长为4的等边中,,分别为,的中点,于点,为的中点,连接,则的长为 .
17.如图,在Rt△ABC中,∠C=90°,AC=1,BC=2,D为AB的中点,E为边BC上一点,将△ADE沿DE翻折得到△A'DE,A'D与BC交于F.若△A'DE与△BDE重叠部分的面积占△ABE面积的,则BF的长为 .
18.如图,在中,,将平移5个单位长度得到,点、分别是、的中点,的最小值等于 .
三、解答题
19.如图所示,点E,F,G,H分别是四边形的边的中点,求证:四边形是平行四边形.
20.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若DE∥AB交AC于点E,证明:△ADE是等腰三角形;
(2)若BC=12,DE=5,且E为AC中点,求AD的值.
21.如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12cm,DE=4cm,求四边形DEFB的周长.
22.在Rt△ABC中,∠BAC=90°,E,F分别是AB,AC上的点,且EF∥BC,作EG平分∠AEF交AC于点G,在EF上取点D,使ED=EA,连接DG并延长,交BA的延长于点P,连接PF.
(1)求证:PD⊥EF;
(2)若ED=DF,求∠B的大小.
(3)在(2)的条件下,若四边形AEDG的面积为S,请直接写出△PEF的面积(用含S的式子表示).
23.如图,直线与轴相交于点,直线经过点,与轴交于点,与轴交于点,与直线相交于点.
求直线的函数关系式;
点是上的一点,若的面积等于的面积的倍,求点的坐标.
设点 的坐标为,是否存在 的值使得 最小?若存在,请求出点 的坐标;若不存在,请说明理由.
24.(1)探究:如图(1),点P在线段AB上,在AB的同侧作△APC和△BPD,满足PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G分别是AC、BD、CD边中点,连接EF、FG、EG.求证:∠EFG=∠GEF.
(2)应用:如图(2),点P在线段AB上方,∠APC=∠BPD=90°,图(1)题中的其他条件不变,若EF=2,则四边形ABDC的面积为 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据等腰三角形的性质和中位线的性质求解即可.
【详解】∵AD=AC,
∴是等腰三角形,
∵AE⊥CD,
∴,
∴E是CD的中点,
∵F是BC的中点,
∴EF是△BCD的中位线,
∴,
故答案为:C.
【点睛】本题考查了三角形的线段长问题,掌握等腰三角形的性质和中位线的性质是解题的关键.
2.B
【分析】根据直角三角形的斜边的中线等于斜边的一半,得到DF=5,由三角形中位线的性质得到DE=8,最后由线段的和差解题即可.
【详解】解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=5,
∵BC= 16,D、E分别是AB,AC的中点,
∴DE=BC=8,
∴EF=DE-DF=3,
故选:B.
【点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.
3.C
【分析】根据三角形两边之差小于第三边、中位线定理、平行四边形的判定方法依次即可求解.
【详解】解:选项A:三角形的两边之差小于第三边,故选项A正确,不符合题意;
选项B:三角形的中位线平行且等于第三边的一半,故选项B正确,不符合题意;
选项C:一个角的两边分别平行另一个角的两边,则这两个角相等或互补,故选项C不正确,是假命题,符合题意;
选项D:一组对边平行且相等的四边形是平行四边形,故选项D正确,不符合题意;
故选:C.
【点睛】本题考查了三角形中位线定理,三角形三边之间的关系,平行四边形的判定等知识点,熟练掌握各个基本定理和性质是解决本类题的关键.
4.B
【分析】根据等腰三角形的性质得到BD=DC,根据三角形中位线定理求出DE,根据三角形的周长公式计算,得到答案.
【详解】解:∵AB=AC,AD平分∠BAC,
∴,
∵点E为AC的中点,
∴,
∴△CDE的周长=CD+CE+DE=17,
故选:B.
【点睛】本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
5.A
【分析】先由三角形的中位线定理推知四边形EFGH是平行四边形,然后求解即可.
【详解】解:如图,
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知:
EF∥AC,GH∥AC且EF=GH=AC,EH=FG=BD,
∴四边形EFGH是平行四边形,
∵四边形EFGH的周长是3,即EF+GH+EH+FG=3,
∴AC+BD=3,
故选:A.
【点睛】本题主要考查中点四边形,解题时,利用三角形中位线定理判定四边形EFGH是平行四边形是解题的关键.
6.D
【分析】根据题意可知DE是AC的垂直平分线,由此即可一一判断.
【详解】∵DE是AC的垂直平分线,
∴DA=DC,AE=EC,故A正确,
∴DE∥BC,∠A=∠DCE,故B正确,
∴∠ADE=∠CDE=∠DCB,故C正确,
故选D.
【点睛】本题考查作图-基本作图、线段的垂直平分线的性质、等腰三角形的性质,三角形中位线定理等知识,解题的关键是熟练运用这些知识解决问题.
7.D
【分析】过D作DG∥AB,交CE于G,连接DE,根据三角形中位线的定理可得CG=EG,通过△DGF △AEF,可得AF=DF,再利用三角形的面积可求解.
【详解】过D作DG∥AB,交CE于G,连接DE,
∵D为BC的中点,
∴DG为△BCE的中位线,
∴BE=2GD,CG=EG,
∵,
∴AE=GD,
∵DG∥AB,
∴∠AEF=∠DGF,∠EAF=∠GDF,
∴△DGF △AEF,
∴AF=DF,
∵,
∴S△ABD=30,S△AED=10,
∴S△AEF=5,
∴S四边形DCEF=S△ABD S△AEF=30 5=25,
故选:D.
【点睛】本题主要考查三角形的面积,全等三角形的判定与性质,三角形的中位线,添加辅助线,构造全等三角形,是解题的关键.
8.A
【分析】根据三角形中位线的性质可知的周长的周长,的周长的周长,以此类推找出规律,写出代数式,再整理即可选择.
【详解】解:∵以△ABC的各边的中点为顶点作,
∴的周长的周长.
∵以各边的中点为顶点作,
∴的周长的周长,
…,
∴的周长
故选:A.
【点睛】本题主要考查三角形中位线的性质,根据三角形中位线的性质求出前2个三角形的面积总结出规律是解答本题的关键.
9.C
【详解】分析:根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和三角形内角和定理即可求出∠PMN的度数.
详解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN,∴△PMN是等腰三角形.
∵∠MPN=130°,∴∠PMN==25°.
故选C.
点睛:本题考查了三角形中位线定理及等腰三角形的判定和性质,解题时要善于根据已知信息,确定应用的知识.
10.B
【分析】根据等腰直角三角形的性质得出∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,求出∠APE=∠CPF,证△APE≌△CPF,推出AE=CF,EP=PF,推出S△AEP=S△CPF,求出S四边形AEPF=S△APC=S△ABC,EF不是△ABC的中位线,故EF≠AP,即可得出答案.
【详解】解:∵△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,
∴∠EPF-∠APF=∠APC-∠APF,
∴∠APE=∠CPF,
在△APE和△CPF中
,
∴△APE≌△CPF(ASA),
∴AE=CF,EP=PF,
∴△EPF是等腰直角三角形,
∴①正确;②正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故③错误;
∵△APE≌△CPF,
∴S△AEP=S△CPF,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=S△APC=S△ABC,
∴④正确;
∴正确的有①②④,
故选:B.
【点睛】本题考查了等腰三角形性质,三角形中位线的性质,三角形三边关系定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.
11.10
【分析】根据三角形中位线定理求出AB,根据直角三角形的性质解答.
【详解】解:∵E、F分别为BC、AC的中点,
∴AB=2EF=20,
∵∠ACB=90°,点D为AB的中点,
∴,
故答案为:10.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
12.
【分析】过点M作于N,则,可得MN是的中位线,利用三角形中位线定理可得MN=AC=3,BN=CN=BC=4,设CF=x,则NF=4-x,由折叠的性质可得MF=CF,在中,利用勾股定理即可求解.
【详解】解:过点M作于N,
∵,,
∴,
∵是的中点,
∴MN是的中位线,
∴MN=AC=3,BN=CN=BC=4,
设CF=x,则NF=4-x,
∵将沿翻折,使与的中点重合,
∴MF=CF=x,
在中,,
∴,解得,
∴CF=.
故答案为:.
【点睛】本题考查折叠的性质,三角形的中位线定理,勾股定理等知识,熟练掌握三角形的中位线定理,利用勾股定理建立方程求解是解题的关键.
13.8
【解析】略
14.
【分析】延长DC交EF于点M(图见详解),根据平行四边形与等边三角形的性质,可证△CFM是等边三角形,BF=BE=EF=BC+CF=5,可求出CF=CM=MF=2,可得C、G是DM和DE的中点,根据中位线的性质,可得出CG=,代入数值即可得出答案.
【详解】解:如下图所示,延长DC交EF于点M,,,
平行四边形的顶点C在等边的边上,
,
是等边三角形,
.
在平行四边形中,,,
又是等边三角形,
,
.
G为的中点,,
是的中点,且是的中位线,
.
故答案为:.
【点睛】本题考查了平行四边形的性质、等边三角形的性质、中位线等知识点,延长DC交EF于点M,利用平行四边形、等边三角形性质求出相应的线段长,证出是的中位线是解题的关键.
15.
【分析】为等边三角形,点A为BF的中点,可得,求得,再证明出点E为AD的中点,得到,可求出面积.
【详解】解:折叠至处,
AB=AF=2cm,BC=BF=CF=4cm,
为等边三角形,
,,
又四边形ABCD为平行四边形,
,
,
cm,CD=AB=2cm,
=,
点A为BF的中点,,
AE为的中位线,
,
点E为AD的中点,
==为折叠重合部分的面积,
故答案为:.
【点睛】本题考查了折叠问题以及等边三角形和平行四边形的综合问题,还涉及勾股定理,需要有一定的推理论证能力,熟练掌握等边三角形和平行四边形的性质是解题的关键.
16.
【分析】连接DE,根据题意可得ΔDEG是直角三角形,然后根据勾股定理即可求解DG的长.
【详解】解:连接DE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=AC.
∵ΔABC是等边三角形,且BC=4,
∴∠DEB=60°,DE=2.
∵EF⊥AC,∠C=60°,EC=2,
∴∠FEC=30°,EF=.
∴∠DEG=180°-60°-30°=90°.
∵G是EF的中点,
∴EG=.
在RtΔDEG中,DG=.
故答案为.
【点睛】本题主要考查了等边三角形的性质,勾股定理以及三角形中位线性质定理,记住和熟练运用性质是解题的关键.
17.##
【分析】依据勾股定理可得AB的长,由△DEF与△ABE面积关系推出F为BE中点,再根据三角形中位线定理以及勾股定理即可得出CE的长,进而得到BF的长.
【详解】解:如图,
Rt△ABC中,∠C=90°,AC=1,BC=2,
∴,
∵点D是AB的中点,
∴S△BDE=S△ABE,
又∵△DEF的面积占△ABE面积的,
∴S△FDE=S△ABE=S△DBE,
∴F是BE的中点,
又∵D是AB的中点,
∴DF是△ABE的中位线,
∴DF∥AE,
∴∠2=∠3,
又∵∠2=∠1,
∴∠1=∠3,
∴AE=AD=AB=,
Rt△ACE中,,
∴BE=2﹣=,
∴BF=BE=,
故答案为:.
【点睛】本题考查勾股定理、三角形中位线定理、折叠图形的特征等知识点,将题目中三角形面积关系转化为线段间的关系是解题关键.
18.
【分析】取A1B1的中点P′,连接QP′、PP′,如图,根据平移的性质得到PP′=7,B1C1=BC=4,再利用P′Q为△A1B1C1的中位线得到P′Q=2,利用三角形三边的关系得到PP′﹣P′Q≤PQ≤PP′+P′Q(当且仅当P、P′、Q三点共线时取等号),从而得到PQ的最小值.
【详解】解:取A1B1的中点P′,连接QP′、PP′,如图:
∵△ABC平移5个单位长度得到△A1B1C1,
∴PP′=5,B1C1=BC=3,
∵Q是A1C1的中点,P′为A1B1的中点,
∴P′Q为△A1B1C1的中位线,
∴P′Q=B1C1=,
∴PP′﹣P′Q≤PQ≤PP′+P′Q(当且仅当P、P′、Q三点共线时取等号),
即,,
∴PQ的最小值为.
故答案为
【点睛】本题主要考查平移的性质和三角形三边关系,三角形的中位线的性质,掌握三角形三边关系是解题的关键.
19.见解析
【分析】连接BD,利用三角形的中位线定理证明得出,从而得到四边形是平行四边形
【详解】解:如图,连接.
∵点E,H分别是线段的中点,
∴是的中位线,
∴EH∥BD,.
同理,.
∴,
∴四边形是平行四边形.
【点睛】此题主要考查了三角形中位线定理和平行四边形的判定方法,题目比较典型,又有综合性,难度不大,解题的关键是正确的添加辅助线,把四边形的问题转化为三角形的问题.
20.(1)见解析;(2)8
【分析】(1)根据“三线合一”性质先推出∠BAD=∠CAD,再结合平行线的性质推出∠BAD=∠ADE,从而得到∠ADE=∠EAD,即可根据“等角对等边”证明;
(2)根据题意结合中位线定理可先推出AC=2DE,然后在Rt△ADC中利用勾股定理求解即可.
【详解】(1)证:∵在△ABC中,AB=AC,
∴△ABC为等腰三角形,
∵AD⊥BC于点D,
∴由“三线合一”知:∠BAD=∠CAD,
∵DE∥AB交AC于点E,
∴∠BAD=∠ADE,
∴∠CAD=∠ADE,
即:∠ADE=∠EAD,
∴AE=DE,
∴△ADE是等腰三角形;
(2)解:由“三线合一”知:BD=CD,
∵BC=12,
∴DC=6,
∵E为AC中点,
∴DE为△ABC的中位线,
∴AB=2DE,
∴AC=AB=2DE=10,
在Rt△ADC中,,
∴AD=8.
【点睛】本题考查等腰三角形的性质与判定,勾股定理解三角形,以及三角形的中位线定理等,掌握等腰三角形的基本性质,熟练运用中位线定理和勾股定理计算是解题关键.
21.(1)见解析;(2)平行四边形DEFB的周长=
【分析】(1)证DE是△ABC的中位线,得DE∥BC,BC=2DE,再证DE=BF,即可得出四边形DEFB是平行四边形;
(2)由(1)得:BC=2DE=8(cm),BF=DE=4cm,四边形DEFB是平行四边形,得BD=EF,再由勾股定理求出BD=10(cm),即可求解.
【详解】(1)证明:∵点D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE//BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
∴四边形DEFB是平行四边形;
(2)解:由(1)得:BC=2DE=8(cm),BF=DE=4cm,四边形DEFB是平行四边形,
∴BD=EF,
∵D是AC的中点,AC=12cm,
∴CD=AC=6(cm),
∵∠ACB=90°,
∴BD==10(cm),
∴平行四边形DEFB的周长=2(DE+BD)=2(4+10)=28(cm).
【点睛】本题考查了平行四边形的判定与性质、三角形中位线定理、勾股定理等知识;熟练掌握三角形中位线定理,证明四边形DEFB为平行四边形是解题的关键.
22.(1)详见解析;(2)60°;(3)S△PEF=3S.
【分析】(1)由“SAS”可证△AEG≌△DEG,可得∠GAE=∠GDE=90°,可得PD⊥EF;
(2)由线段垂直平分线的性质可得EG=GF,可得∠GFE=∠GEF,由直角三角形的性质可求∠AEG=∠GEF=∠GFE=30°,由平行线的性质可求解;
(3)先证△PEF是等边三角形,可证四边形AEDG的面积=S△AEF=S△PEF,即可求解.
【详解】(1)∵EG平分∠AEF,
∴∠AEG=∠DEG,
在△AEG和△DEG中,
,
∴△AEG≌△DEG(SAS)
∴∠GAE=∠GDE=90°,
∴PD⊥EF;
(2)∵ED=DF,PD⊥EF,
∴EG=GF,
∴∠GFE=∠GEF,
∴∠AEG=∠GEF=∠GFE,
∵∠AEG+∠GEF+∠GFE=90°,
∴∠AEG=∠GEF=∠GFE=30°,
∴∠AEF=60°,
∵EF∥BC,
∴∠AEF=∠B=60°
(2)∵ED=DF,PD⊥EF,
∴PE=PF,且∠PEF=60°,
∴△PEF是等边三角形,
∵AF⊥AB,
∴AE=AP,
∴S△AEF=S△AFP,
∵∠BAC=90°,∠AEG=30°,
∴EG=2AG,
∴GF=2AG,
∴2S△AEG=S△EGF,
∵ED=DF,
∴S△GED=S△GFD,
∴S△GED=S△GFD=S△AEG,
∴四边形AEDG的面积=S△AEF=S△PEF,
∴S△PEF=3S.
【点睛】本题考查了三角形的综合问题,掌握全等三角形的性质以及判定定理、线段垂直平分线的性质、直角三角形的性质、平行线的性质是解题的关键.
23.(1)y=x-2;(2)( ,)或(, );(3)(,3).
【分析】(1)把点(3,-1),点B(6,0)代入直线l2,求出k、b的值即可;
(2)设点P的坐标为(t, t-2),求出D点坐标,再由S△ABP=2S△ABD求出t的值即可;
(3)作直线y=3,作点A关于直线y=3的对称点A′,连结A′B,利用待定系数法求出其解析式,根据点Q(m,3)在直线A′B上求出m的值,进而可得出结论.
【详解】解:(1)由题知:
解得:
,
故直线l2的函数关系式为:y=x-2;
(2)由题及(1)可设点P的坐标为(t, t-2).
解方程组 ,得 ,
∴点D的坐标为(,-).
∵S△ABP=2S△ABD,
∴AB |t-2|=2×AB |-|,即|t-2|=,解得:t=或t=,
∴点P的坐标为( ,)或(, );
(3)作直线y=3(如图),再作点A关于直线y=3的对称点A′,连结A′B.
由几何知识可知:A′B与直线y=3的交点即为QA+QB最小时的点Q.
∵点A(3,0),
∴A′(3,6)
∵点B(6,0),
∴直线A′B的函数表达式为y=-2x+12.
∵点Q(m,3)在直线A′B上,
∴3=-2m+12
解得:m=,
故存在m的值使得QA+QB最小,此时点Q的坐标为(,3).
【点睛】此题考查一次函数综合题,涉及到一次函数图象上点的坐标特点,轴对称最短路线问题,三角形的面积公式,解题关键在于在解答(3)时要注意作出辅助线,利用轴对称的性质求解.
24.(1)见解析;(2)4
【分析】(1)连接AD,BC,可证得△APD≌△CPB,从而得到AD=CB.再由三角形中位线定理,可得EG=GF,即可求证;
(2)连接AD、BC交于点M,BC、PD交于点N,可证得△APD≌△CPB,从而得到AD=CB.∠ADP=∠CBP,再由∠CND=∠PNB,AD⊥BC,再由三角形中位线定理,可得△GEF为等腰直角三角形,从而得到,再由,即可求解.
【详解】证明:(1) 如图,连接AD,BC,
∵∠APC=∠BPD,
∴∠APD=∠CPB.
∵PA=PC,PD=PB,
∴△APD≌△CPB,
∴AD=CB.
∵E、G、F分别为AC、CD、DB的中点,
∴EG=AD,GF=BC,
∴EG=GF,
∴∠GEF=∠GFE.
(2)如图,连接AD、BC交于点M,BC、PD交于点N,
∵∠APC=∠BPD=90°,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB,
∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS),
∴AD=CB,∠ADP=∠CBP,
∵∠CND=∠PNB,
∴∠DMN=∠BPD=90°,
∴AD⊥BC,
∵E、G、F分别为AC、CD、DB的中点,
∴EG是△ACD的中位线,GF是△DCB的中位线,
∴EG=AD,GF=BC, EGAD,GFBC,
∴GE=GF,GE⊥GF,
∴△GEF为等腰直角三角形,
∴,
∵EF=2,
∴,
∴.
故答案为:4
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法、等腰直角三角形的性质及三角形中位线的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
