专题18.10三角形的中位线 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.10三角形的中位线 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 21:57:57 | ||
图片预览

文档简介
专题18.10 三角形的中位线(基础篇)(专项练习)
一、单选题
1.如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
A.2 B.4 C.8 D.10
2.如图,在平行四边形中,对角线与相交于点,是边的中点,连接,若,,则的度数为( )
A. B. C. D.
3..如图,矩形中,是的中点,点 在 边上运动,, 分别是 , 的中点,则的长随着点的运动( )
A.变短 B.变长 C.不变 D.无法确定
4.如图,在中,D,E分别是的中点,点F在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
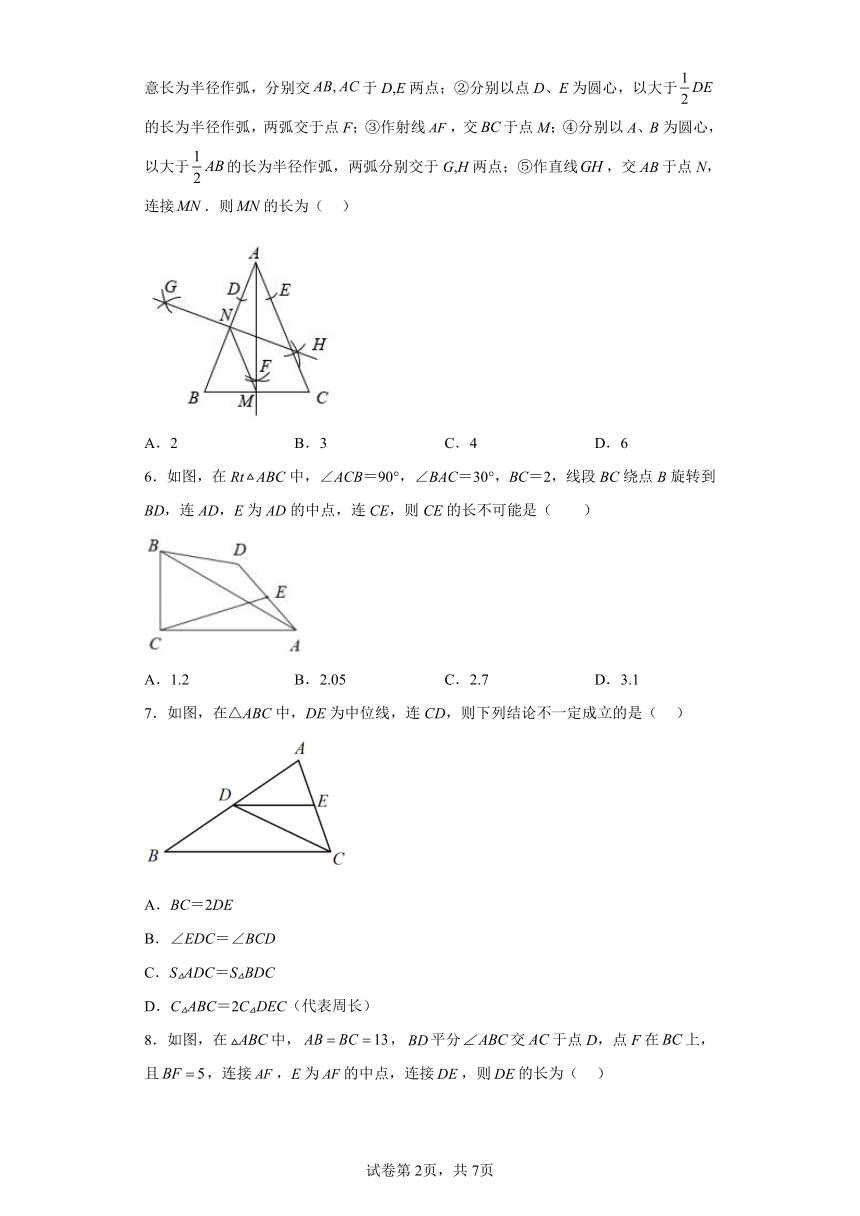
5.如图,等腰三角形中,,按以下要求作图:①以点A为圆心,任意长为半径作弧,分别交于D,E两点;②分别以点D、E为圆心,以大于的长为半径作弧,两弧交于点F;③作射线,交于点M;④分别以A、B为圆心,以大于的长为半径作弧,两弧分别交于G,H两点;⑤作直线,交于点N,连接.则的长为( )
A.2 B.3 C.4 D.6
6.如图,在RtABC中,∠ACB=90°,∠BAC=30°,BC=2,线段BC绕点B旋转到BD,连AD,E为AD的中点,连CE,则CE的长不可能是( )
A.1.2 B.2.05 C.2.7 D.3.1
7.如图,在△ABC中,DE为中位线,连CD,则下列结论不一定成立的是( )
A.BC=2DE
B.∠EDC=∠BCD
C.S△ADC=S△BDC
D.C△ABC=2C△DEC(代表周长)
8.如图,在中,,平分交于点D,点F在上,且,连接,E为的中点,连接,则的长为( )
A.3 B.4 C.5 D.6
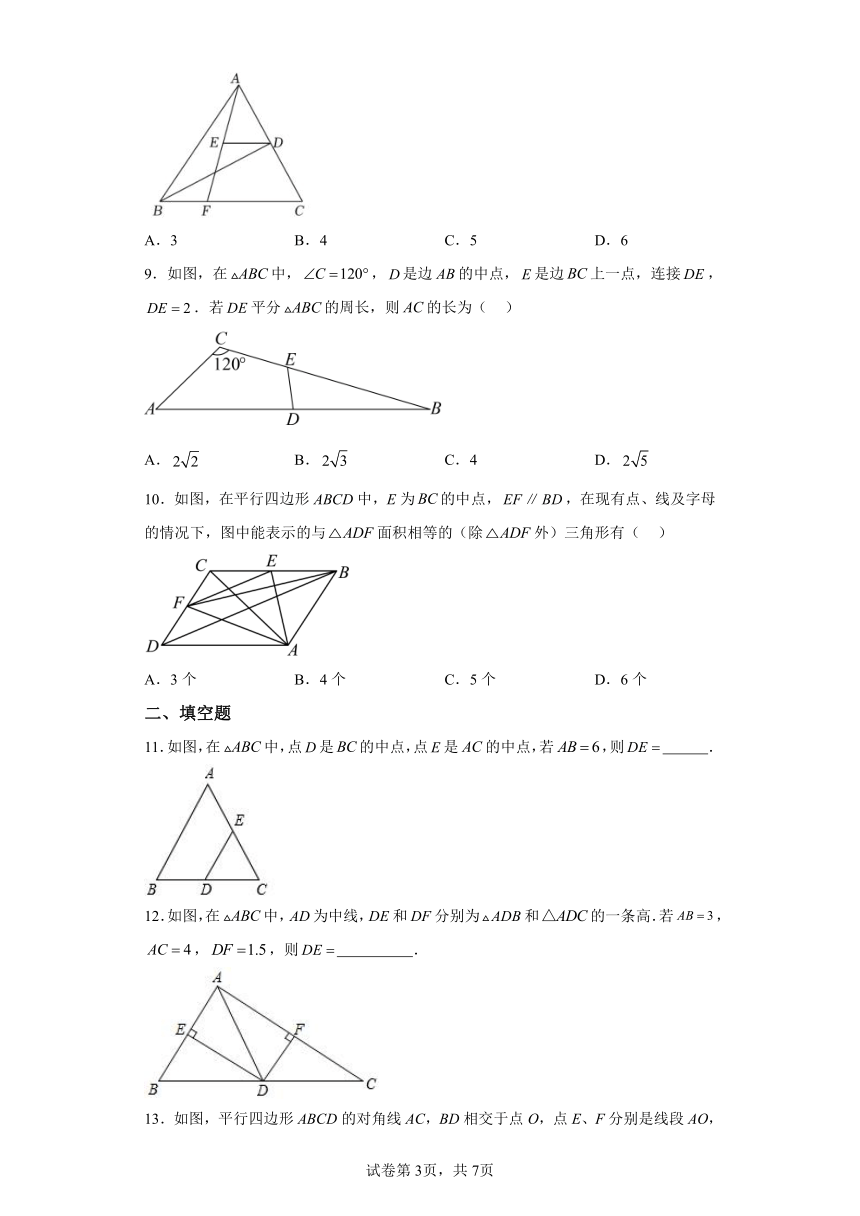
9.如图,在中,,是边的中点,是边上一点,连接,.若平分的周长,则的长为( )
A. B. C.4 D.
10.如图,在平行四边形ABCD中,E为的中点,,在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.如图,在中,点是的中点,点是的中点,若,则 .
12.如图,在中,为中线,和分别为和的一条高.若,,,则 .
13.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E、F分别是线段AO,BO的中点,若AC+BD=12cm,△OAB的周长是10cm,则EF= cm.
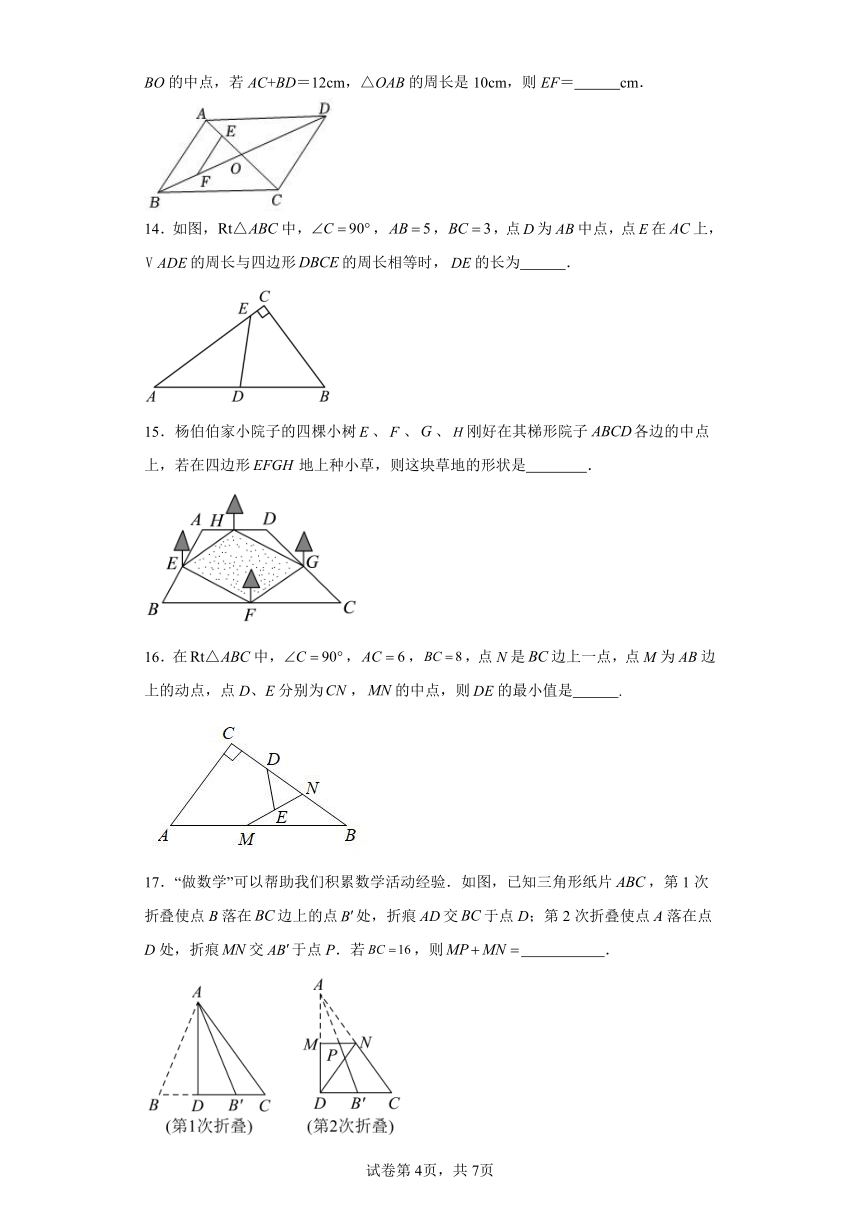
14.如图,中,,,,点为中点,点在上,的周长与四边形的周长相等时,的长为 .
15.杨伯伯家小院子的四棵小树、、、刚好在其梯形院子各边的中点上,若在四边形地上种小草,则这块草地的形状是 .
16.在中,,,,点N是边上一点,点M为边上的动点,点D、E分别为,的中点,则的最小值是 .
17.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片,第1次折叠使点B落在边上的点处,折痕交于点D;第2次折叠使点A落在点D处,折痕交于点P.若,则 .
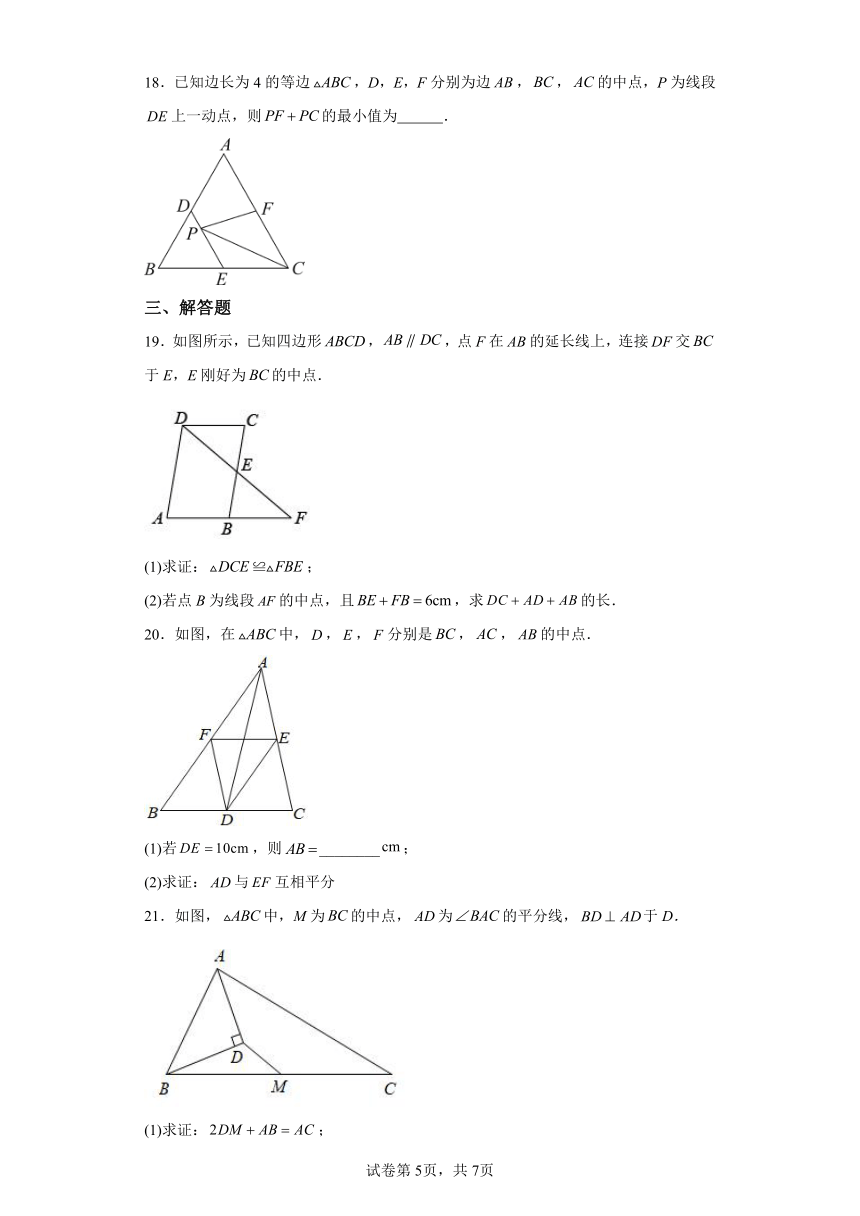
18.已知边长为4的等边,D,E,F分别为边,,的中点,P为线段上一动点,则的最小值为 .
三、解答题
19.如图所示,已知四边形,,点F在的延长线上,连接交于E,E刚好为的中点.
(1)求证:;
(2)若点B为线段的中点,且,求的长.
20.如图,在中,,,分别是,,的中点.
(1)若,则________;
(2)求证:与互相平分
21.如图,中,M为的中点,为的平分线,于D.
(1)求证:;
(2)若,求的长.
22.已知中,,点D、E、F分别是的边的中点,连接;求证:.
23.如图,平行四边形ABCD的对角线AC,BD交于点O,M,N分别是AB,AD的中点.
(1)求证:四边形AMON是平行四边形;
(2)若AC=6,BD=4,∠AOB=90°,求NO的长度.
24.公股定理神奇而美丽,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:两个全等的直角三角板 和直角三角板 ,顶点F在边止,顶点C、D重合,连接 、.设、交于点G., , ( ),. 请你回答以下问题:
(1)请猜想与的位置关系,并加以证明.
(2)填空: =___________(用含有c的代数式表示)
(3)请尝试利用此图形证明勾股定理.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据三角形中位线定理计算即可.
【详解】解:∵D、E分别是AB、AC边上的中点,DE=4,
∴BC=2DE=2×4=8,
故选:C.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
2.D
【分析】根据三角形的内角和可求的,根据平行四边形的性质以及三角形中位线的性质,可得,根据两直线平行内错角相等即可求得.
【详解】解:,,
,
四边形是平行四边形,对角线与相交于点O,
,
E是边的中点,
∴,
故选D
【点睛】本题考查了三角形的内角和定理,平行四边形的性质,三角形中位线的性质,掌握平行四边形的性质是解题的关键.
3.C
【分析】易得EF为的中位线,那么EF长恒等于定值AR的一半.
【详解】解:∵E,F分别是AM,MR的中点,
∴,
∴无论M运动到哪个位置EF的长不变,
故选:C.
【点睛】本题考查三角形中位线等于第三边的一半的性质.
4.B
【分析】利用三角形中位线定理得到DE∥AC,结合平行四边形的判定定理对各个选项进行判断即可.
【详解】解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
A.根据∠B=∠F不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
B.∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
C.根据AC=CF不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
故选:B.
【点睛】本题考查了平行四边形的判定、三角形的中位线定理以及平行线的判定等知识;熟练掌握平行四边形的判定和三角形中位线定理是解题的关键.
5.B
【分析】根据作图过程可得AM平分∠BAC,GH是边AB的垂直平分线,由等腰三角形三线合一,得AM是边BC上的中线,可得MN是△ABC的中位线,进而可得MN的长.
【详解】解:根据作图过程可知:AM平分∠BAC,GH是边AB的垂直平分线,
∵AB=AC=6,AM平分∠BAC,
∴AM是边BC上的中线,
∴BM=CM,
∵GH是边AB的垂直平分线,
∴AN=BN,
∴MN是△ABC的中位线,
∴MNAC=3.
故选:B.
【点睛】此题考查了作图﹣复杂作图,角平分线的性质,线段垂直平分线的性质,等腰三角形的性质,熟知角平分线的作法是解题的关键.
6.D
【分析】取AB的中点F,得到△BCF是等边三角形,利用三角形中位线定理推出EF=BD=1,再分类讨论求得,即可求解.
【详解】解:取AB的中点F,连接EF、CF,
∵∠BAC=30°,BC=2,
∴AB=2BC=4,BF=FA=BC=CF=2,∠ABC=60°,
∴△BCF是等边三角形,
∵E、F分别是AD、AB的中点,
∴EF=BD=1,
如图:
当C、E、F共线时CE有最大值,最大值为CF+EF=3;
如图,
当C、E、F共线时CE有最小值,最小值为CF-EF=1;
∴,
观察各选项,只有选项D符合题意,
故选:D.
【点睛】本题考查了等边三角形的判定和性质,三角形中位线定理,分类讨论求得CE的取值范围是解题的关键.
7.D
【分析】由在△ABC中,DE为中位线,可得DE∥BC,DE=,即BC=2DE,可判断选项A;由DE∥BC,内错角相等可得∠EDC=∠BCD,可判断选项B;由DE为△ABC的中位线,可得D为AB中点,可得AD=BD,过C作CH⊥AB于H,由CH是△BCD的高,也是△ACD的高,根据三角形面积等底同高可得S△ADC= S△BDC,可判断选项C;由CD为AB边中线,当∠ACB=90°,或∠ACB≠90°时,分类考虑C△ABC= 2C△DEC,或C△ABC≠2C△DEC,可判断选项D.
【详解】解:∵在△ABC中,DE为中位线,
∴DE∥BC,DE=,
∴BC=2DE,
∴选项A正确,不符合题意;
∵DE∥BC,
∴∠EDC=∠BCD,
故选项B正确,不符合题意;
∵DE为△ABC的中位线,
∴D为AB中点,
∴AD=BD,
过C作CH⊥AB于H,
∴CH是△BCD的高,也是△ACD的高,
∴S△ADC=,
S△BDC=,
∴S△ADC= S△BDC,
故选项C正确,不符合题意;
∵CD为AB边中线,
当∠ACB=90°时,
∴AB=2CD,
∵BC=2DE,点E为AC中点,
∴AC=2EC,
∵C△ABC=AB+BC+CA=2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC= 2C△DEC,
当∠ACB≠90°时,
AB≠2CD,
∴C△ABC=AB+BC+CA≠2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC≠2C△DEC,
∴选项D的结论不一定成立,符合题意.
故选择D.
【点睛】本题考查三角形中位线性质,中线性质,平行线性质,三角形周长关系,掌握三角形中位线性质,中线性质,平行线性质,三角形周长关系是解题关键.
8.B
【分析】根据等腰三角形的性质可得,为的中点,通过中位线的性质可得,,求解即可.
【详解】解:由题意可得:,
∵,平分,
∴为中线,即为的中点,
又∵E为的中点,
∴为的中位线,
∴,
故选:B
【点睛】此题考查了等腰三角形的性质,三角形中位线的性质,解题的关键是熟练掌握相关基础性质.
9.C
【分析】延长至,使得,连接,构造等边三角形,根据题意可得是的中位线,即可求解.
【详解】解:如图,延长至,使得,连接,
,
,
又,
是等边三角形,
,
是边的中点,是边上一点,平分的周长,
,,
,
,
,
即,
是的中位线,,
.
故选C.
【点睛】本题考查了三角形中位线的性质与判定,等边三角形的性质,三角形中线的定义,构造等边三角形是解题的关键.
10.C
【分析】找面积相等的三角形即找到等底等高的三角形即可.
【详解】 E为的中点,,
F为中点,
四边形ABCD为平行四边形,
,,
是的中线,是的中线,是的中线,
,
能表示的与面积相等的(除外)三角形有5个,
故选:C.
【点睛】本题考查中位线的性质、平行四边形的性质、中线的性质,熟记三角形的中线把一个三角形分成面积相等的两部分是解题的关键.
11.3
【分析】利用三角形中位线定理可直接求得DE的长度.
【详解】解:∵点D为BC的中点,点E为AC的中点,
∴DE是△ABC的中位线,
∴DE=AB=×6=3.
故答案为:3.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
12.2
【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.
【详解】解:∵△ABC中,AD为中线,
∴BD=DC,
∴S△ABD=S△ADC,
∵DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,
∴ AB ED= AC DF,
∴×3×ED=×4×1.5,
∴ED=2,
故答案为:2.
【点睛】此题考查三角形的中线,三角形的中线把三角形的面积分成相等的两部分.本题的解答充分利用了面积相等这个点.
13.2
【分析】根据平行四边形的性质得到,求出OA+OB的值,由△OAB的周长求出AB,根据三角形中位线的性质求出EF的长.
【详解】解:∵四边形ABCD是平行四边形,
∴,
∵AC+BD=12cm,
∴,
∵△OAB的周长是10cm,
∴OA+OB+AB=10cm,
∴AB=4cm,
∵点E、F分别是线段AO,BO的中点,
∴,
故答案为:2
【点睛】此题考查了平行四边形的性质,三角形中位线是判定及性质,熟记平行四边形的性质是解题的关键.
14.
【分析】中,勾股定理求出AC,由的周长与四边形的周长相等,推出AE=3.5,CE=0.5,过点D作DF⊥AC于F,得DF=BC=1.5,EF=1.5,即可求出DE.
【详解】解:中,,,,
∴AC=4,
∵点为中点,
∴AD=BD,
∵的周长与四边形的周长相等,
∴AD+DE+AE=BD+DE+BC+CE,
∴AE=BC+CE,
∵AE+BC+CE=4+3=7,
∴AE=3.5,CE=0.5,
过点D作DF⊥AC于F,
∴AF=CF=2,DF=BC=1.5,
∴EF=1.5,
∴DE=,
故答案为:.
【点睛】此题考查了勾股定理,三角形中位线的性质,三角形中线性质,正确掌握三角形中线的性质求出CE是解题的关键.
15.平行四边形
【分析】根据中位线定理可知,四边形EFGH的对边平行且相等,所以四边形EFGH是平行四边形.
【详解】解:连接AC,BD.
利用三角形的中位线定理可得EH∥FG,EH=FG.
∴这块草地的形状是平行四边形.
故答案为:平行四边形.
【点睛】本题考查的知识点为:一组对边平行且相等的四边形是平行四边形,注意结合实际.
16.##2.4##
【分析】连接,根据三角形中位线的性质得出,只要找到的最小值即可,根据垂线段最短可知当时,最短,此时利用勾股定理和三角形的面积公式即可求解.
【详解】解:连接CM,
∵点D、E分别为,的中点,
∴.
当时,的值最小,此时的值也最小.
由勾股定理得:.
∵,
∴,
∴,
故答案为:.
【点睛】本题主要考查了三角形中位线定理,垂线段最短,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
17.8
【分析】先把图补全,由折叠得:证明是的中位线,得,可得答案.
【详解】
解:如图,由折叠图得:
,
,
∴是的中位线,
,
,
.
故答案为:8.
【点睛】本题考查了三角形的中位线定理,折叠的性质,把图形补全证明是的中位线是解本题的关键.
18.4
【分析】连接,,设交于点J,根据等边三角形的性质及中位线的性质得出, ,由三角形三边关系即可得出结果.
【详解】解:如图,连接,,设交于点J,
∵是等边三角形,D、E、F分别为边、、的中点,
∴,,,
∴, ,
∴是线段的垂直平分线,
∴,
∴,
∵,
∴,
∴的最小值为4,
故答案为:4.
【点睛】本题主要考查等边三角形的性质及中位线的性质,三角形的三边关系等,理解题意,综合运用这些知识点是解题关键.
19.(1)见解析;
(2).
【分析】(1)利用平行线的性质,可得,即可求证;
(2)根据三角形中位线的性质,可得,由(1)可得,则
【详解】(1)证明:∵,
∴,
∵为的中点,
∴,
又∵,
∴;
(2)解:∵为的中点,点B为线段的中点,
∴为的中位线,,
∴,
由(1)得,
∴,即,
∴.
【点睛】此题考查了全等三角形的判定与性质,三角形中位线的性质,平行线的性质,解题的关键是熟练掌握相关基础性质.
20.(1)20
(2)见解析
【分析】(1)根据中位线的性质即可求解;
(2)证明四边形是平行四边形即可得出结论.
【详解】(1)解:∵,分别是,的中点
∴,
,
∴,
故答案为:;
(2)证明:,,分别是,,的中点,
四边形是平行四边形,
∴与互相平分.
【点睛】本题考查了三角形中位线的性质与判定,平行四边形的性质与判定,掌握三角形中位线的性质是解题的关键.
21.(1)证明见解析;
(2)14
【分析】(1)延长,交于点E,通过证明≌,得到,,进而得到为的中位线,即可得证;
(2)利用勾股定理得到线段的长度,再结合(1)的结论,即可求出线段的长度.
【详解】(1)解:如图,延长,交于点E,
∵平分,
∴,
在与中,
∴≌,
∴,,
即点D为线段的中点,
∴为的中位线,
∴,
∵,
∴;
(2)解:在中,,
∴.
【点睛】本题考查全等三角形的判定与性质、中位线的定义及性质,根据题目的提示,正确做出辅助线,构造出全等三角形是解题的关键.
22.见解析
【分析】由直角三角形斜边上的中线等于斜边的一半可以得到,由中位线定理得到,等量代换即可得到结论.
【详解】证明:F是的边的中点,
,
点D、E是边的中点,
是的中位线,
,
.
【点睛】本题考查直角三角形斜边中线的性质,三角形中位线的性质,熟练掌握三角形的中位线定理是解题的关键.
23.(1)证明见解析;(2).
【分析】(1)根据平行四边形的性质得到AO=OC,BO=OD,根据三角形中位线的性质得到MO∥AD,NO∥AB,根据平行四边形的判定可证得结论;
(2)由勾股定理求得AB,根据三角形中位线的性质得到进而可得结论.
【详解】(1)∵四边形是平行四边形,
∴AO=OC,BO=OD.
∵,分别是、的中点,
∴,,
∴,,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,.
∵,,
∴,.
∵,
∴.
∵是的中点,,
∴,
∴.
【点睛】本题主要考查了平行四边形的性质和判定,三角形中位线的性质,勾股定理,根据三角形中位线的性质得到是解决问题的关键.
24.(1),见解析
(2)
(3)见解析
【分析】(1)根据全等三角形的性质得到 ,求得 ,得到 ,根据垂直的定义可得.
(2)根据三角形的面积公式即可得到结论.
(3)根据三角形面积和梯形面积公式用两种方法求得四边形 的面积,可得到结论.
【详解】(1)解:
证明:
(2)解:
=
故答案为:
(3)解: =
即
【点睛】本题考查了勾股定理的证明,三角形面积的计算,全等三角形的性质,正确识别图形是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
A.2 B.4 C.8 D.10
2.如图,在平行四边形中,对角线与相交于点,是边的中点,连接,若,,则的度数为( )
A. B. C. D.
3..如图,矩形中,是的中点,点 在 边上运动,, 分别是 , 的中点,则的长随着点的运动( )
A.变短 B.变长 C.不变 D.无法确定
4.如图,在中,D,E分别是的中点,点F在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
5.如图,等腰三角形中,,按以下要求作图:①以点A为圆心,任意长为半径作弧,分别交于D,E两点;②分别以点D、E为圆心,以大于的长为半径作弧,两弧交于点F;③作射线,交于点M;④分别以A、B为圆心,以大于的长为半径作弧,两弧分别交于G,H两点;⑤作直线,交于点N,连接.则的长为( )
A.2 B.3 C.4 D.6
6.如图,在RtABC中,∠ACB=90°,∠BAC=30°,BC=2,线段BC绕点B旋转到BD,连AD,E为AD的中点,连CE,则CE的长不可能是( )
A.1.2 B.2.05 C.2.7 D.3.1
7.如图,在△ABC中,DE为中位线,连CD,则下列结论不一定成立的是( )
A.BC=2DE
B.∠EDC=∠BCD
C.S△ADC=S△BDC
D.C△ABC=2C△DEC(代表周长)
8.如图,在中,,平分交于点D,点F在上,且,连接,E为的中点,连接,则的长为( )
A.3 B.4 C.5 D.6
9.如图,在中,,是边的中点,是边上一点,连接,.若平分的周长,则的长为( )
A. B. C.4 D.
10.如图,在平行四边形ABCD中,E为的中点,,在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.如图,在中,点是的中点,点是的中点,若,则 .
12.如图,在中,为中线,和分别为和的一条高.若,,,则 .
13.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E、F分别是线段AO,BO的中点,若AC+BD=12cm,△OAB的周长是10cm,则EF= cm.
14.如图,中,,,,点为中点,点在上,的周长与四边形的周长相等时,的长为 .
15.杨伯伯家小院子的四棵小树、、、刚好在其梯形院子各边的中点上,若在四边形地上种小草,则这块草地的形状是 .
16.在中,,,,点N是边上一点,点M为边上的动点,点D、E分别为,的中点,则的最小值是 .
17.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片,第1次折叠使点B落在边上的点处,折痕交于点D;第2次折叠使点A落在点D处,折痕交于点P.若,则 .
18.已知边长为4的等边,D,E,F分别为边,,的中点,P为线段上一动点,则的最小值为 .
三、解答题
19.如图所示,已知四边形,,点F在的延长线上,连接交于E,E刚好为的中点.
(1)求证:;
(2)若点B为线段的中点,且,求的长.
20.如图,在中,,,分别是,,的中点.
(1)若,则________;
(2)求证:与互相平分
21.如图,中,M为的中点,为的平分线,于D.
(1)求证:;
(2)若,求的长.
22.已知中,,点D、E、F分别是的边的中点,连接;求证:.
23.如图,平行四边形ABCD的对角线AC,BD交于点O,M,N分别是AB,AD的中点.
(1)求证:四边形AMON是平行四边形;
(2)若AC=6,BD=4,∠AOB=90°,求NO的长度.
24.公股定理神奇而美丽,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:两个全等的直角三角板 和直角三角板 ,顶点F在边止,顶点C、D重合,连接 、.设、交于点G., , ( ),. 请你回答以下问题:
(1)请猜想与的位置关系,并加以证明.
(2)填空: =___________(用含有c的代数式表示)
(3)请尝试利用此图形证明勾股定理.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据三角形中位线定理计算即可.
【详解】解:∵D、E分别是AB、AC边上的中点,DE=4,
∴BC=2DE=2×4=8,
故选:C.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
2.D
【分析】根据三角形的内角和可求的,根据平行四边形的性质以及三角形中位线的性质,可得,根据两直线平行内错角相等即可求得.
【详解】解:,,
,
四边形是平行四边形,对角线与相交于点O,
,
E是边的中点,
∴,
故选D
【点睛】本题考查了三角形的内角和定理,平行四边形的性质,三角形中位线的性质,掌握平行四边形的性质是解题的关键.
3.C
【分析】易得EF为的中位线,那么EF长恒等于定值AR的一半.
【详解】解:∵E,F分别是AM,MR的中点,
∴,
∴无论M运动到哪个位置EF的长不变,
故选:C.
【点睛】本题考查三角形中位线等于第三边的一半的性质.
4.B
【分析】利用三角形中位线定理得到DE∥AC,结合平行四边形的判定定理对各个选项进行判断即可.
【详解】解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
A.根据∠B=∠F不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
B.∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
C.根据AC=CF不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
故选:B.
【点睛】本题考查了平行四边形的判定、三角形的中位线定理以及平行线的判定等知识;熟练掌握平行四边形的判定和三角形中位线定理是解题的关键.
5.B
【分析】根据作图过程可得AM平分∠BAC,GH是边AB的垂直平分线,由等腰三角形三线合一,得AM是边BC上的中线,可得MN是△ABC的中位线,进而可得MN的长.
【详解】解:根据作图过程可知:AM平分∠BAC,GH是边AB的垂直平分线,
∵AB=AC=6,AM平分∠BAC,
∴AM是边BC上的中线,
∴BM=CM,
∵GH是边AB的垂直平分线,
∴AN=BN,
∴MN是△ABC的中位线,
∴MNAC=3.
故选:B.
【点睛】此题考查了作图﹣复杂作图,角平分线的性质,线段垂直平分线的性质,等腰三角形的性质,熟知角平分线的作法是解题的关键.
6.D
【分析】取AB的中点F,得到△BCF是等边三角形,利用三角形中位线定理推出EF=BD=1,再分类讨论求得,即可求解.
【详解】解:取AB的中点F,连接EF、CF,
∵∠BAC=30°,BC=2,
∴AB=2BC=4,BF=FA=BC=CF=2,∠ABC=60°,
∴△BCF是等边三角形,
∵E、F分别是AD、AB的中点,
∴EF=BD=1,
如图:
当C、E、F共线时CE有最大值,最大值为CF+EF=3;
如图,
当C、E、F共线时CE有最小值,最小值为CF-EF=1;
∴,
观察各选项,只有选项D符合题意,
故选:D.
【点睛】本题考查了等边三角形的判定和性质,三角形中位线定理,分类讨论求得CE的取值范围是解题的关键.
7.D
【分析】由在△ABC中,DE为中位线,可得DE∥BC,DE=,即BC=2DE,可判断选项A;由DE∥BC,内错角相等可得∠EDC=∠BCD,可判断选项B;由DE为△ABC的中位线,可得D为AB中点,可得AD=BD,过C作CH⊥AB于H,由CH是△BCD的高,也是△ACD的高,根据三角形面积等底同高可得S△ADC= S△BDC,可判断选项C;由CD为AB边中线,当∠ACB=90°,或∠ACB≠90°时,分类考虑C△ABC= 2C△DEC,或C△ABC≠2C△DEC,可判断选项D.
【详解】解:∵在△ABC中,DE为中位线,
∴DE∥BC,DE=,
∴BC=2DE,
∴选项A正确,不符合题意;
∵DE∥BC,
∴∠EDC=∠BCD,
故选项B正确,不符合题意;
∵DE为△ABC的中位线,
∴D为AB中点,
∴AD=BD,
过C作CH⊥AB于H,
∴CH是△BCD的高,也是△ACD的高,
∴S△ADC=,
S△BDC=,
∴S△ADC= S△BDC,
故选项C正确,不符合题意;
∵CD为AB边中线,
当∠ACB=90°时,
∴AB=2CD,
∵BC=2DE,点E为AC中点,
∴AC=2EC,
∵C△ABC=AB+BC+CA=2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC= 2C△DEC,
当∠ACB≠90°时,
AB≠2CD,
∴C△ABC=AB+BC+CA≠2CD+2DE+2CE=2(CD+DE+EC)=2C△DEC,
∴C△ABC≠2C△DEC,
∴选项D的结论不一定成立,符合题意.
故选择D.
【点睛】本题考查三角形中位线性质,中线性质,平行线性质,三角形周长关系,掌握三角形中位线性质,中线性质,平行线性质,三角形周长关系是解题关键.
8.B
【分析】根据等腰三角形的性质可得,为的中点,通过中位线的性质可得,,求解即可.
【详解】解:由题意可得:,
∵,平分,
∴为中线,即为的中点,
又∵E为的中点,
∴为的中位线,
∴,
故选:B
【点睛】此题考查了等腰三角形的性质,三角形中位线的性质,解题的关键是熟练掌握相关基础性质.
9.C
【分析】延长至,使得,连接,构造等边三角形,根据题意可得是的中位线,即可求解.
【详解】解:如图,延长至,使得,连接,
,
,
又,
是等边三角形,
,
是边的中点,是边上一点,平分的周长,
,,
,
,
,
即,
是的中位线,,
.
故选C.
【点睛】本题考查了三角形中位线的性质与判定,等边三角形的性质,三角形中线的定义,构造等边三角形是解题的关键.
10.C
【分析】找面积相等的三角形即找到等底等高的三角形即可.
【详解】 E为的中点,,
F为中点,
四边形ABCD为平行四边形,
,,
是的中线,是的中线,是的中线,
,
能表示的与面积相等的(除外)三角形有5个,
故选:C.
【点睛】本题考查中位线的性质、平行四边形的性质、中线的性质,熟记三角形的中线把一个三角形分成面积相等的两部分是解题的关键.
11.3
【分析】利用三角形中位线定理可直接求得DE的长度.
【详解】解:∵点D为BC的中点,点E为AC的中点,
∴DE是△ABC的中位线,
∴DE=AB=×6=3.
故答案为:3.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
12.2
【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.
【详解】解:∵△ABC中,AD为中线,
∴BD=DC,
∴S△ABD=S△ADC,
∵DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,
∴ AB ED= AC DF,
∴×3×ED=×4×1.5,
∴ED=2,
故答案为:2.
【点睛】此题考查三角形的中线,三角形的中线把三角形的面积分成相等的两部分.本题的解答充分利用了面积相等这个点.
13.2
【分析】根据平行四边形的性质得到,求出OA+OB的值,由△OAB的周长求出AB,根据三角形中位线的性质求出EF的长.
【详解】解:∵四边形ABCD是平行四边形,
∴,
∵AC+BD=12cm,
∴,
∵△OAB的周长是10cm,
∴OA+OB+AB=10cm,
∴AB=4cm,
∵点E、F分别是线段AO,BO的中点,
∴,
故答案为:2
【点睛】此题考查了平行四边形的性质,三角形中位线是判定及性质,熟记平行四边形的性质是解题的关键.
14.
【分析】中,勾股定理求出AC,由的周长与四边形的周长相等,推出AE=3.5,CE=0.5,过点D作DF⊥AC于F,得DF=BC=1.5,EF=1.5,即可求出DE.
【详解】解:中,,,,
∴AC=4,
∵点为中点,
∴AD=BD,
∵的周长与四边形的周长相等,
∴AD+DE+AE=BD+DE+BC+CE,
∴AE=BC+CE,
∵AE+BC+CE=4+3=7,
∴AE=3.5,CE=0.5,
过点D作DF⊥AC于F,
∴AF=CF=2,DF=BC=1.5,
∴EF=1.5,
∴DE=,
故答案为:.
【点睛】此题考查了勾股定理,三角形中位线的性质,三角形中线性质,正确掌握三角形中线的性质求出CE是解题的关键.
15.平行四边形
【分析】根据中位线定理可知,四边形EFGH的对边平行且相等,所以四边形EFGH是平行四边形.
【详解】解:连接AC,BD.
利用三角形的中位线定理可得EH∥FG,EH=FG.
∴这块草地的形状是平行四边形.
故答案为:平行四边形.
【点睛】本题考查的知识点为:一组对边平行且相等的四边形是平行四边形,注意结合实际.
16.##2.4##
【分析】连接,根据三角形中位线的性质得出,只要找到的最小值即可,根据垂线段最短可知当时,最短,此时利用勾股定理和三角形的面积公式即可求解.
【详解】解:连接CM,
∵点D、E分别为,的中点,
∴.
当时,的值最小,此时的值也最小.
由勾股定理得:.
∵,
∴,
∴,
故答案为:.
【点睛】本题主要考查了三角形中位线定理,垂线段最短,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
17.8
【分析】先把图补全,由折叠得:证明是的中位线,得,可得答案.
【详解】
解:如图,由折叠图得:
,
,
∴是的中位线,
,
,
.
故答案为:8.
【点睛】本题考查了三角形的中位线定理,折叠的性质,把图形补全证明是的中位线是解本题的关键.
18.4
【分析】连接,,设交于点J,根据等边三角形的性质及中位线的性质得出, ,由三角形三边关系即可得出结果.
【详解】解:如图,连接,,设交于点J,
∵是等边三角形,D、E、F分别为边、、的中点,
∴,,,
∴, ,
∴是线段的垂直平分线,
∴,
∴,
∵,
∴,
∴的最小值为4,
故答案为:4.
【点睛】本题主要考查等边三角形的性质及中位线的性质,三角形的三边关系等,理解题意,综合运用这些知识点是解题关键.
19.(1)见解析;
(2).
【分析】(1)利用平行线的性质,可得,即可求证;
(2)根据三角形中位线的性质,可得,由(1)可得,则
【详解】(1)证明:∵,
∴,
∵为的中点,
∴,
又∵,
∴;
(2)解:∵为的中点,点B为线段的中点,
∴为的中位线,,
∴,
由(1)得,
∴,即,
∴.
【点睛】此题考查了全等三角形的判定与性质,三角形中位线的性质,平行线的性质,解题的关键是熟练掌握相关基础性质.
20.(1)20
(2)见解析
【分析】(1)根据中位线的性质即可求解;
(2)证明四边形是平行四边形即可得出结论.
【详解】(1)解:∵,分别是,的中点
∴,
,
∴,
故答案为:;
(2)证明:,,分别是,,的中点,
四边形是平行四边形,
∴与互相平分.
【点睛】本题考查了三角形中位线的性质与判定,平行四边形的性质与判定,掌握三角形中位线的性质是解题的关键.
21.(1)证明见解析;
(2)14
【分析】(1)延长,交于点E,通过证明≌,得到,,进而得到为的中位线,即可得证;
(2)利用勾股定理得到线段的长度,再结合(1)的结论,即可求出线段的长度.
【详解】(1)解:如图,延长,交于点E,
∵平分,
∴,
在与中,
∴≌,
∴,,
即点D为线段的中点,
∴为的中位线,
∴,
∵,
∴;
(2)解:在中,,
∴.
【点睛】本题考查全等三角形的判定与性质、中位线的定义及性质,根据题目的提示,正确做出辅助线,构造出全等三角形是解题的关键.
22.见解析
【分析】由直角三角形斜边上的中线等于斜边的一半可以得到,由中位线定理得到,等量代换即可得到结论.
【详解】证明:F是的边的中点,
,
点D、E是边的中点,
是的中位线,
,
.
【点睛】本题考查直角三角形斜边中线的性质,三角形中位线的性质,熟练掌握三角形的中位线定理是解题的关键.
23.(1)证明见解析;(2).
【分析】(1)根据平行四边形的性质得到AO=OC,BO=OD,根据三角形中位线的性质得到MO∥AD,NO∥AB,根据平行四边形的判定可证得结论;
(2)由勾股定理求得AB,根据三角形中位线的性质得到进而可得结论.
【详解】(1)∵四边形是平行四边形,
∴AO=OC,BO=OD.
∵,分别是、的中点,
∴,,
∴,,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,.
∵,,
∴,.
∵,
∴.
∵是的中点,,
∴,
∴.
【点睛】本题主要考查了平行四边形的性质和判定,三角形中位线的性质,勾股定理,根据三角形中位线的性质得到是解决问题的关键.
24.(1),见解析
(2)
(3)见解析
【分析】(1)根据全等三角形的性质得到 ,求得 ,得到 ,根据垂直的定义可得.
(2)根据三角形的面积公式即可得到结论.
(3)根据三角形面积和梯形面积公式用两种方法求得四边形 的面积,可得到结论.
【详解】(1)解:
证明:
(2)解:
=
故答案为:
(3)解: =
即
【点睛】本题考查了勾股定理的证明,三角形面积的计算,全等三角形的性质,正确识别图形是解题的关键.
答案第1页,共2页
答案第1页,共2页
