专题18.14平面直角坐标系背景下的平行四边形 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.14平面直角坐标系背景下的平行四边形 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 00:00:00 | ||
图片预览


文档简介
专题18.14 平面直角坐标系背景下的平行四边形
(巩固篇)(专项练习)
一、单选题
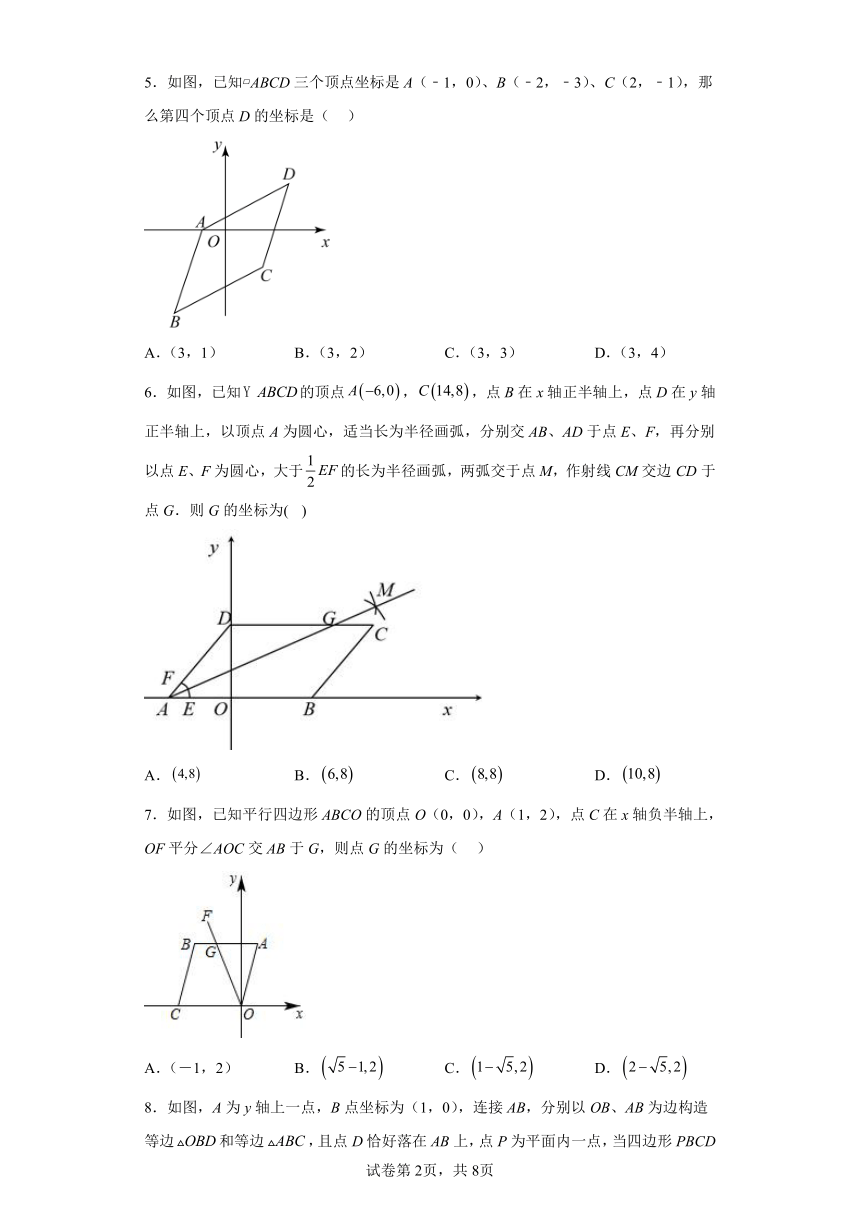
1.平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA=OC=,则点B的坐标为( )
A.(,1) B.(1,) C.(+1,1) D.(1,+1)
2.如图,点A的坐标为(1,3),点B在x轴上,把沿x轴向右平移到,若四边形ABDC的面积为9,则点C的坐标为( )
A.(1,4) B.(3,4) C.(3,3) D.(4,3)
3.如图,△OAB的顶点O、A、B的坐标分别是(0,0)(3,0),(1,1),下列点M中,O、A、B、M为顶点的四边形不是平行四边形的是( )
A.(1,﹣1) B.(2,﹣1) C.(﹣2,1) D.(4,1)
4.在平面直角坐标系中,以为顶点构成平行四边形,下列各点不能作为平行四边形顶点的是( )
A. B. C. D.
5.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是( )
A.(3,1) B.(3,2) C.(3,3) D.(3,4)
6.如图,已知的顶点,,点B在x轴正半轴上,点D在y轴正半轴上,以顶点A为圆心,适当长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点M,作射线CM交边CD于点G.则G的坐标为( )
A. B. C. D.
7.如图,已知平行四边形ABCO的顶点O(0,0),A(1,2),点C在x轴负半轴上,OF平分∠AOC交AB于G,则点G的坐标为( )
A.(-1,2) B. C. D.
8.如图,A为y轴上一点,B点坐标为(1,0),连接AB,分别以OB、AB为边构造等边和等边,且点D恰好落在AB上,点P为平面内一点,当四边形PBCD为平行四边形时,点P坐标为( )
A. B. C. D.
9.如图1,在中,,,动点从出发,沿匀速运动到点.图2是点运动时,的面积随点运动路程变化的关系图像,则的值是( )
A.2 B.3 C.4 D.6
10.如图,点,的坐标分别为,,点为平面直角坐标系内一点,,点为线段的中点,连接,则的最小值为( )
A. B. C. D.
二、填空题
11.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是 .
12.在平面直角坐标系中,A(﹣1,3),B(2,3),C(1,﹣3).若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标可能是 .
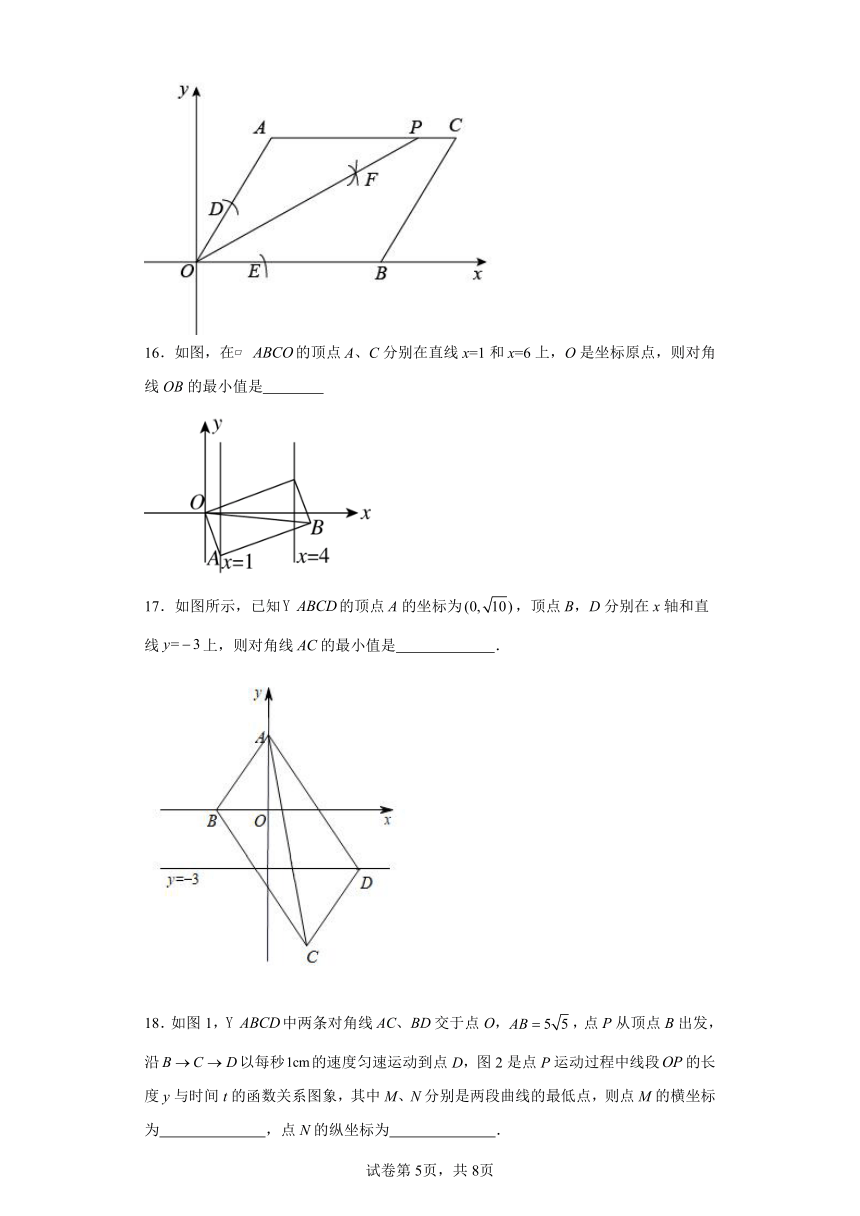
13.已知,平行四边形OABC在平面直角坐标系的位置如图所示,点A在x轴上,对角线AC,OB交于点D.分别以点O,点B为圆心,以大于的长为半径画弧,两弧交于点E,连接DE交BC于点F.若点A(6,0),点C(2,4),则点F的坐标为 .
14.如图,在平面直角坐标系中,平行四边形OABC的顶点O(0,0),点A在x轴的正半轴上,∠COA的平分线OD交BC于点D(2,3),则点C的坐标为 .
15.如图,在平面直角坐标系中,的顶点B在x轴上,点A坐标为,以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E,再分别以点D,点E为圆心,以大于的长为半径作弧,两弧在∠AOB内相交于点F,作射线OF交AC于点P.则点P的坐标是 .
16.如图,在 的顶点A、C分别在直线x=1和x=6上,O是坐标原点,则对角线OB的最小值是
17.如图所示,已知的顶点A的坐标为,顶点B,D分别在x轴和直线上,则对角线的最小值是 .
18.如图1,中两条对角线交于点O,,点P从顶点B出发,沿以每秒的速度匀速运动到点D,图2是点P运动过程中线段的长度y与时间t的函数关系图象,其中M、N分别是两段曲线的最低点,则点M的横坐标为 ,点N的纵坐标为 .
三、解答题
19.如图,在平面直角坐标系中,四边形各顶点的坐标分别为,,,,现将四边形经过平移后得到四边形,点的对应点的坐标为.
(1)请直接写点、、的坐标;
(2)求四边形与四边形重叠部分的面积;
(3)在轴上是否存在一点,连接、,使,若存在这样一点,求出点的坐标;若不存在,请说明理由.
20.如图1,平面直角坐标系中,轴,,C是点A关于x轴的对称点,,交x轴于点E,连接.
(1)求证:
①平分;
②是等边三角形;
(2)如图2,若F在上,,连接,点B的坐标为,直接写出点F的坐标(用a、b表示).
21.如图,已知点、、.
(1)将绕点О逆时针旋转90°得,画出,并写出点C的对应点的坐标为__________.
(2)画出关于原点成中心对称的图形.
(3)在平面直角坐标系内找点D,使得A、B、C、D为顶点的四边形为平行四边形,则点D的坐标为__________.
22.如图在平面直角坐标系中,,,轴且,点从点出发,以1个单位长度的速度向点运动;点从点同时出发,以2个单位长度的速度向点运动,规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为秒.
(1)当四边形是平行四边形时,求的值;
(2)当时,求的值;
(3)当恰好垂直平分时,求的值.
23.如图1,在平面直角坐标系中,A、B两点的坐标分别是(m,0)和(0,n),m、n满足,点C在y轴上,四边形ABCD是平行四边形,AC与BD交于点E.
(1)直接写出A、B两点的坐标;
(2)如图1,若点C在y轴负半轴上,且AB=BC,求点E的坐标;
(3)如图2,若点C与原点O重合,OH⊥BD于H,M为AB的中点,求MH的长.
24.如图1 ,在平面直角坐标系中,点A、B的坐标分别为,,现同时将A、B向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接、、.
(1)写出C、D的坐标并求出四边形的面积.
(2)在x 轴上 是否存在一点F,使得三角形的面积是三角形面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图 2、3、4,点 P 是直线上的一个动点,连接、,当点P在直线上运动时,请直接写出与、的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】作,求得、的长度,即可求解.
【详解】解:作,如下图:
则
在平行四边形中,,
∴
∴为等腰直角三角形
则,解得
∴
故选:C
【点睛】此题考查了平行四边形的性质,等腰直角三角形的性质以及勾股定理,解题的关键是灵活运用相关性质进行求解.
2.D
【分析】根据平移的性质得出四边形ABDC是平行四边形,从而得A和C的纵坐标相同,根据四边形ABDC的面积求得AC的长,即可求得C的坐标.
【详解】解:∵把△OAB沿x轴向右平移到△ECD,
∴四边形ABDC是平行四边形,
∴AC=BD,A和C的纵坐标相同,
∵四边形ABDC的面积为9,点A的坐标为(1,3),
∴3AC=9,
∴AC=3,
∴C(4,3),
故选:D.
【点睛】本题考查了坐标与图形的变换-平移,平移的性质,平行四边形的性质,求得平移的距离是解题的关键.
3.A
【分析】分三种情况讨论:①AB为对角线时,②OB为对角线时,③OA为对角线时;分别求出点的坐标,即可得出答案.
【详解】分三种情况:
①AB为对角线时,
∵BM∥OA,点O、A、B的坐标分别是(0,0)(3,0),(1,1),
∴M的坐标为(3+1,1),
即M(4,1);
②OB为对角线时,
∵,点O、A、B的坐标分别是(0,0)(3,0),(1,1),
∴的坐标为(1﹣3,1),
即M(﹣2,1);
③OA为对角线时,点与关于原点O对称,
∴的坐标为(2,﹣1),
即M(2,-1);
综上所述,点M的坐标为(4,1)或(﹣2,1)或(2,﹣1),
故选:A.
【点睛】本题考查了平行四边形的判定与性质、坐标与图形性质以及分类讨论等知识;正确画出图形是解题的关键.
4.B
【分析】分别以AC、AB、BC为对角线画平行四边形,再分别写出个点的坐标,即可选出答案.
【详解】解:如图所示:
①以AC为对角线,可以画出 AFCB,F(-3,1);
②以AB为对角线,可以画出 ACBE,E(5,1);
③以BC为对角线,可以画出 ACDB,D(1,-1);
故选:B.
【点睛】此题主要考查了平行四边形的判定,坐标与图形,关键是分类讨论,正确画出图形.
5.B
【分析】过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,求出△DCN≌△BAE,根据全等三角形的性质得出BE=DN,AE=CN,根据A、B、C的坐标求出OM和DM即可.
【详解】解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
,
∴△DCN≌△BAE(AAS),
∴BE=DN,AE=CN,
∵A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),
∴CN=AE=2﹣1=1,DN=BE=3,
∴DM=3﹣1=2,OM=2+1=3,
∴D的坐标为(3,2),
故选:B.
【点睛】本题考查了全等三角形的性质和判定,平行四边形的性质,点的坐标与图形性质等知识点,能正确作出辅助线是解题的关键.
6.D
【分析】先根据平行四边形的性质和角平分线的作图方法证得AD=DG,结合坐标与图形性质求得OA、OD,再根据勾股定理求得AD即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠DGA=∠BAG,
由作图过程知,AM平分∠DAB,
∴∠DAG=∠BAG,
∴∠DAG=∠DGA,
∴DG=AD,
∵,,
∴OA=6,D(0,8)即OD=8,
∴在Rt△AOD中,AD==10,
∴DG=10,
∴G的坐标为(10,8),
故选:D.
【点睛】本题考查尺规作图-作角平分线、平行四边形的性质、平行线的性质、等角对等边、勾股定理、坐标与图形,熟练掌握相关知识的联系与运用是解答的关键.
7.C
【分析】过点G作GD⊥x轴,根据点的坐标得出AO=,利用平行四边形的性质及角平分线得出∠AOG=∠AGO,由等角对等边得出AO=AG=,结合图形确定GE=,yG=yA=2,即可确定点的坐标.
【详解】解:过点G作GD⊥x轴,同时标注字母如图所示:
∵A(1,2),
∴AO=,
∵四边形AOCB为平行四边形,
∴AB∥OC,
∴∠AGO=∠COG,
∵OF平分∠AOC,
∴∠AOG=∠COG,
∴∠AOG=∠AGO,
∴AO=AG=,
∴GE=,
yG=yA=2,
点G在第二象限,
G(),
故选:C.
【点睛】题目主要考查坐标与图形,平行四边形的性质,勾股定理,角平分线的定义,等角对等边等,理解题意,综合运用这些知识点是解题关键.
8.B
【分析】利用等边三角形的性质可得点D和C的坐标,再利用平行四边形的性质可得P的坐标.
【详解】如图,
以OB、AB为边构造等边△OBD和等边△ABC,
∴∠ODB=∠OBD=60,OB=1,∠CAB=60°,
∴∠OAB=30°,
∴∠OAD=∠DOA=30°,
∴OD=AD=1,
∵点D为AB的中点,
∴AB=2,AO=,
∴,
∴∠CAO=90°,
∴,
∵四边形PBCD是平行四边形,
∴DPBC,DP=BC,
由平移可知,
故选:B.
【点睛】本题主要考查了等边三角形的性质,平行四边形的性质,平移的性质等知识,利用平移的性质得出点P的坐标是解题的关键.
9.D
【分析】过D点作DE⊥BC于点F,根据图像可得平行四边形的边长CD为4,再利用平行四边形的面积可求a.
【详解】如图,当点运动到与点重合时,过点作的垂线,交的延长线于点.
由题意知,当点在上运动时,的面积不变,
此时,.
∵,,
∴,
∴.
【点睛】本题主要考查平行四边形动点问题,函数图像,平行四边形的性质,解题的关键是结合两个图像,随着动点的运动找到对应的函数图像.
10.D
【分析】连接,取中点,连接,根据三角形任意两边之和大于第三边求最值即可.
【详解】解:连接,取中点,连接,
∵,
∴当取最大值时,三点共线,即在之间,
即,
∵分别是的中点,
∴,
∵,
∴,
∴,
∴,
故选:D.
【点睛】本题考查三角形的三边关系,中位线定理,平面直角坐标系中的点与几何,勾股定理,能够熟练掌握数形结合思想是解决本题的关键.
11.(3,2)
【分析】连接AC,BD,两线交于点M,设D点坐标为,利用中点坐标公式即可求解.
【详解】连接AC,BD,两线交于点M,如图,
∵四边形ABCD是平行四边形,
∴对角线AC、BD的交点M为AC、BD的中点,
∵,,,
设D点坐标为,
∴根据中点坐标公式有:,
解得,
∴ D点坐标为,
故答案为:.
【点睛】本题主要考查了平行四边形的性质、中点坐标公式的知识,掌握中点坐标公式是解答本题的关键.
12.(4,﹣3)或(0,9)或(﹣2,﹣3)
【分析】分三种情况:①BC为对角线时,②AB为对角线时,③AC为对角线时,由平行四边形的性质容易得出点D的坐标.
【详解】解:∵A(-1,3),B(2,3),
∴AB=3,轴,
分三种情况:①BC为对角线时, 如图1,
∵四边形ABCD是平行四边形,
∴,AB=CD,
∴轴,
∵AB=3,C(1,-3),
∴点D的坐标为(4,-3)
②AC为对角线时,如图2,
∵四边形ABCD是平行四边形,
∴,AB=CD,
∴轴,
∵AB=3,C(1,﹣3),
∴点D的坐标为(﹣2,﹣3)
③AB为对角线时,如图3,
连接CD交AB于E,
设D的坐标为(x,y),
∵四边形ABCD是平行四边形,
∴E分别为AB、CD的中点,
∵A(-1,3),B(2,3),C(1,-3),
∴,
解得,
∴点D的坐标为(0,9),
综上所述,点D的坐标可能是(4,-3)或(0,9)或(-2,-3).
【点睛】本题考查了平行四边形的性质、坐标与图形的性质;熟练掌握平行四边形的性质是解决问题的关键.
13.(3,4)
【分析】连接OF,延长BC交y轴于点M,则轴,由题意可知,,,.根据平行四边形的性质及作图过程,可知DE垂直平分线段OB,即有,设,则,,然后在中,利用勾股定理可列方程,解得,即,结合图形即可确定F点坐标.
【详解】解:如图,连接OF,延长BC交y轴于点M,则轴,
∵四边形OABC为平行四边形,
∴D为对角线OB中点,
由题意可知,,,,
由作图可知,DE垂直平分线段OB,
∴,
设,则,,
在中,,
即,解得,
∴,
∴点F的坐标为(3,4).
故答案为:(3,4).
【点睛】本题主要考查了平行四边形的性质、图形与坐标、垂直平分线和勾股定理的知识,解题关键是熟练掌握平行四边形的性质.
14.
【分析】先利用平行四边形的性质和角平分线定义得到CO=CD,再设出C点坐标,建立方程即可.
【详解】解:∵四边形OABC是平行四边形,
∴BCOA,
∴∠CDO=∠DOA,
∵OD平分∠COA,
∴∠COD=∠DOA,
∠COD=∠CDO,
∴CO=CD,
∴
设C(m,3),
∴,
解得:,
∴,
故答案为:.
【点睛】本题考查了角平分线的定义和平行四边形的性质,涉及到了勾股定理建立方程的知识,解题关键是正确建立方程并求解,本题蕴含了数形结合的思想.
15.##
【分析】利用勾股定理先求解 再证明 从而可得答案.
【详解】解:∵点A坐标为,
∴
∵,
由作图可得:平分
故答案为:
【点睛】本题考查的是平行四边形的性质,勾股定理的应用,角平分线的作图与计算,等腰三角形的判定,理解题意,证明是解本题的关键.
16.7
【分析】过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E.则由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,即可得出答案.
【详解】解:过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,
直线x=6与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OCAB,OA=BC,
∵直线x=1与直线x=6均垂直于x轴,
∴AMCN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,
,
∴△OAF≌△BCD(ASA).
∴BD=OF=1,
∴OE=6+1=7,
∴
∵OE的长不变,
∴当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=7.
故答案为7.
【点睛】本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质,勾股定理;熟练掌握平行四边形的性质,勾股定理,证明三角形全等是解决问题的关键.
17.##
【分析】设点C坐标为(a,b),由平行四边形的性质可求b=,可得点C在直线y=上运动,再根据点C在y轴上时,AC的长度有最小值求解即可.
【详解】解:设点C坐标为(a,b),
∵顶点B、D分别在x轴和直线y= 3上,
∴点B,点D的纵坐标分别为0, 3,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴,
∴b=,
∴点C在直线y=上运动,
∴当点C在y轴上时,AC的长度有最小值,
∴对角线AC的最小值为:,
故答案为:.
【点睛】本题考查了平行四边形的性质,坐标与图形性质,确定点C的运动轨迹是本题的关键.
18. 10
【分析】由图可知点P在BC上运动时,OP先变小后变大,求出OP的最大值和最小值,过O作于点,则可求得OB=OD= ,OC= ;而从C向D运动时,OP先变小后变大,过点O作于点,利用勾股定理求解即可.
【详解】解:由图可知点P在BC上运动时,OP先变小后变大,
由图象可知:点P从B向C运动时,OP的最大值为,最小值为5,,
∴,
由于M是曲线部分的最低点,
∴此时OP最小,
如下图,过O作于点,,
∴由勾股定理可知:,
∴点M的横坐标为10;
过点O作于点,如下图,
∵四边形ABCD是平行四边形,
∴OD=OB,CD=AB,
由图象可知:点P从C向D运动时,,又,
∴设,则,
∴,
∴,
即,
∴,
∴点N的纵坐标为.
故答案为:10,.
【点睛】本题考查了动点与函数图象的理解和应用、平行四边形的性质、勾股定理.把图形和图象结合理解得到线段长度是解决本题的关键.
19.(1)
(2)
(3)存在,或
【分析】(1)先确定平移的规则,然后根据平移的规则求出点、、的坐标即可;
(2)由平移的性质可知重叠部分为平行四边形且高为2,再根据相似三角形的判定与性质求得底,然后求出面积即可;
(3)设点的坐标为,先求出平行四边形ABCD的面积,然后利用三角形的面积公式即可求出b的值.
【详解】(1)解:∵,,
∴平移的规则为:向右平移2个单位,向上平移一个单位;
∵,,,
∴;
(2)解:如图,延长交x轴于点E,过点做
由平移可知,重叠部分为平行四边形,底边长为3,高为2
∵
即
∴重叠部分的面积为
(3)解:存在;
设点的坐标为,
∵,
,
∴,
∴点的坐标为或.
【点睛】本题主要考查了平移的性质、平行四边形的性质、坐标与图形、求阴影部分的面积等知识点,熟练掌握平移的性质是解题的关键.
20.(1)①见解析;②见解析;
(2).
【分析】(1)①利用平行线的性质和等腰三角形的性质证明即可证明结论;②先根据对称性得到,进而证明,.证明∴.得到,即可证明是等边三角形;
(2)如图所示,过点B作轴于G,过点F作于H,由等边三角形的性质得到,证明四边形是平行四边形,得到,,再由,,证明,得到,利用勾股定理和含30度角的直角三角形的性质求出,则,,同理,据此即可得到答案.
【详解】(1)证明:(1)①∵,
∴.
∵轴,
∴.
∴.
∴平分;
②C是点A关于x轴的对称点,
∴.
∵
∴.
∴.
∴.
在和中
∴.
∴.
∴是等边三角形.
(2)解:如图所示,过点B作轴于G,过点F作于H,
∴,
∵是等边三角形,
∴,
∴,
∵,
∴四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
同理,即,
∴;
【点睛】本题主要考查了坐标与图形,平行线的性质,三角形内角和定理,等边对等角,全等三角形的性质与判定,平行四边形的性质与判定,等边三角形的性质与判定,含30度角的直角三角形的性质,勾股定理等等,灵活运用所学知识是解题的关键.
21.(1)见解析,
(2)见解析
(3)或或
【分析】(1)根据网格结构找出点绕O点逆时针旋转后的对应点的位置,然后顺次连接即可,再根据平面直角坐标系写出点的坐标;
(2)利用关于原点对称的点的坐标特征写出点的对应点的坐标,然后描点即可得到;
(3)根据平行四边形的判定进行求解即可.
【详解】(1)如图,即为所求,点的坐标为.
故答案为:
(2)即为所求;
(3)如图,满足条件的点D的坐标为或或.
故答案为或或.
【点睛】本题考查旋转变换,平行四边形的判定等知识,解题的关键是熟练掌握基本知识.
22.(1)
(2)或
(3)
【分析】(1)利用平行四边形的性质构建方程即可解决问题.
(2)分两种情形:四边形是平行四边形,四边形是等腰梯形,分别求解即可.
(3)利用线段垂直平分线的性质构建方程即可解决问题.
【详解】(1)∵,
∴当时,四边形是平行四边形,
∵,,
∴,
∴
(2)①当四边形是平行四边形时,,
∴,
∴
②当四边形是等腰梯形时,,
此时,
∵,
∴,
∴,
∴
综上,或
(3)∵,
∴.
当垂直平分时,则,
∴,
解得
【点睛】本题考查了平行四边形的判定与性质,等腰梯形,线段垂直平分线的性质,坐标与图形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,利用参数构建方程解决问题.
23.(1)A(4,0),B(0,4)
(2)E(2,)
(3)MH=
【分析】(1)利用非负性求出m、n的值即可得到A、B两点的坐标;
(2)根据AB=BC求出C点坐标,利用平行四边形的性质和中点坐标公式即可求出点E的坐标;
(3)根据等积法和勾股定理求出OH和BH,根据OH和BH求出H点的坐标,再结合M点的坐标即可求出MH的长.
【详解】(1)解:∵
即:
∴
∴ A(4,0),B(0,4)
(2)解:∵OB=OA=4
∴AB=
∴BC=AB=,OC=BC-OB=
C点坐标为(0,)
∵点E是AC中点,
∴,
∴E(2,).
(3)解:∵C与O重合,
∴E为OA的中点,
∴OE=2,
∴BE=,
∵
即:
∴OH=,
∴BH==
设H点的坐标为(x,y)则:
由①-②得:,解得:
把代入①得:或(舍)
∴H
又∵M为AB的中点,
∴M(2,2)
∴MH.
【点睛】本题考查坐标系和几何的综合应用.本题的综合性较强,利用非负性、平行四边形的性质和中点坐标公式,以及勾股定理进行解题.
24.(1)8;
(2)存在,点的坐标为或;
(3)当点在线段的延长线上运动时,; 当点在线段的延长线上运动时,;当点在线段上运动时,.
【分析】(1)根据点的平移规律可得,的坐标,然后利用即可求出四边形的面积;
(2)根据的面积是面积的2倍,得,即可求出点的坐标;
(3)当点在线段延长线上运动时,作,当点在线段的延长线上时,作,当点在线段上运动时,作,分别根据平行线的性质和平行线间的传递性求解即可.
【详解】(1)解:∵点,的坐标分别为、,
∴将点,分别向上平移2个单位长度,再向右平移1个单位长度,得到,的对应点,,
∴,,,,,
∴四边形的面积为:
.
∴点的坐标为,点的坐标为,四边形的面积为.
(2)存在,
如图,设,
∵,,
∴,
又∵的面积是面积的2倍.
∴,
∴,
∵,
∴,
解得:或,
∴点的坐标为或.
(3)当点在线段延长线上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
当点在线段的延长线上时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
当点在线段上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
综上所述:当点在线段的延长线上运动时,;
当点在线段的延长线上运动时,;
当点在线段上运动时,.
【点睛】本题考查平行线的判定和性质,点平移的规律,梯形的面积,三角形的面积等知识点.对点的位置进行分类讨论是解题的关键.
答案第1页,共2页
答案第1页,共2页
(巩固篇)(专项练习)
一、单选题
1.平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA=OC=,则点B的坐标为( )
A.(,1) B.(1,) C.(+1,1) D.(1,+1)
2.如图,点A的坐标为(1,3),点B在x轴上,把沿x轴向右平移到,若四边形ABDC的面积为9,则点C的坐标为( )
A.(1,4) B.(3,4) C.(3,3) D.(4,3)
3.如图,△OAB的顶点O、A、B的坐标分别是(0,0)(3,0),(1,1),下列点M中,O、A、B、M为顶点的四边形不是平行四边形的是( )
A.(1,﹣1) B.(2,﹣1) C.(﹣2,1) D.(4,1)
4.在平面直角坐标系中,以为顶点构成平行四边形,下列各点不能作为平行四边形顶点的是( )
A. B. C. D.
5.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是( )
A.(3,1) B.(3,2) C.(3,3) D.(3,4)
6.如图,已知的顶点,,点B在x轴正半轴上,点D在y轴正半轴上,以顶点A为圆心,适当长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点M,作射线CM交边CD于点G.则G的坐标为( )
A. B. C. D.
7.如图,已知平行四边形ABCO的顶点O(0,0),A(1,2),点C在x轴负半轴上,OF平分∠AOC交AB于G,则点G的坐标为( )
A.(-1,2) B. C. D.
8.如图,A为y轴上一点,B点坐标为(1,0),连接AB,分别以OB、AB为边构造等边和等边,且点D恰好落在AB上,点P为平面内一点,当四边形PBCD为平行四边形时,点P坐标为( )
A. B. C. D.
9.如图1,在中,,,动点从出发,沿匀速运动到点.图2是点运动时,的面积随点运动路程变化的关系图像,则的值是( )
A.2 B.3 C.4 D.6
10.如图,点,的坐标分别为,,点为平面直角坐标系内一点,,点为线段的中点,连接,则的最小值为( )
A. B. C. D.
二、填空题
11.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是 .
12.在平面直角坐标系中,A(﹣1,3),B(2,3),C(1,﹣3).若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标可能是 .
13.已知,平行四边形OABC在平面直角坐标系的位置如图所示,点A在x轴上,对角线AC,OB交于点D.分别以点O,点B为圆心,以大于的长为半径画弧,两弧交于点E,连接DE交BC于点F.若点A(6,0),点C(2,4),则点F的坐标为 .
14.如图,在平面直角坐标系中,平行四边形OABC的顶点O(0,0),点A在x轴的正半轴上,∠COA的平分线OD交BC于点D(2,3),则点C的坐标为 .
15.如图,在平面直角坐标系中,的顶点B在x轴上,点A坐标为,以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E,再分别以点D,点E为圆心,以大于的长为半径作弧,两弧在∠AOB内相交于点F,作射线OF交AC于点P.则点P的坐标是 .
16.如图,在 的顶点A、C分别在直线x=1和x=6上,O是坐标原点,则对角线OB的最小值是
17.如图所示,已知的顶点A的坐标为,顶点B,D分别在x轴和直线上,则对角线的最小值是 .
18.如图1,中两条对角线交于点O,,点P从顶点B出发,沿以每秒的速度匀速运动到点D,图2是点P运动过程中线段的长度y与时间t的函数关系图象,其中M、N分别是两段曲线的最低点,则点M的横坐标为 ,点N的纵坐标为 .
三、解答题
19.如图,在平面直角坐标系中,四边形各顶点的坐标分别为,,,,现将四边形经过平移后得到四边形,点的对应点的坐标为.
(1)请直接写点、、的坐标;
(2)求四边形与四边形重叠部分的面积;
(3)在轴上是否存在一点,连接、,使,若存在这样一点,求出点的坐标;若不存在,请说明理由.
20.如图1,平面直角坐标系中,轴,,C是点A关于x轴的对称点,,交x轴于点E,连接.
(1)求证:
①平分;
②是等边三角形;
(2)如图2,若F在上,,连接,点B的坐标为,直接写出点F的坐标(用a、b表示).
21.如图,已知点、、.
(1)将绕点О逆时针旋转90°得,画出,并写出点C的对应点的坐标为__________.
(2)画出关于原点成中心对称的图形.
(3)在平面直角坐标系内找点D,使得A、B、C、D为顶点的四边形为平行四边形,则点D的坐标为__________.
22.如图在平面直角坐标系中,,,轴且,点从点出发,以1个单位长度的速度向点运动;点从点同时出发,以2个单位长度的速度向点运动,规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为秒.
(1)当四边形是平行四边形时,求的值;
(2)当时,求的值;
(3)当恰好垂直平分时,求的值.
23.如图1,在平面直角坐标系中,A、B两点的坐标分别是(m,0)和(0,n),m、n满足,点C在y轴上,四边形ABCD是平行四边形,AC与BD交于点E.
(1)直接写出A、B两点的坐标;
(2)如图1,若点C在y轴负半轴上,且AB=BC,求点E的坐标;
(3)如图2,若点C与原点O重合,OH⊥BD于H,M为AB的中点,求MH的长.
24.如图1 ,在平面直角坐标系中,点A、B的坐标分别为,,现同时将A、B向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接、、.
(1)写出C、D的坐标并求出四边形的面积.
(2)在x 轴上 是否存在一点F,使得三角形的面积是三角形面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图 2、3、4,点 P 是直线上的一个动点,连接、,当点P在直线上运动时,请直接写出与、的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】作,求得、的长度,即可求解.
【详解】解:作,如下图:
则
在平行四边形中,,
∴
∴为等腰直角三角形
则,解得
∴
故选:C
【点睛】此题考查了平行四边形的性质,等腰直角三角形的性质以及勾股定理,解题的关键是灵活运用相关性质进行求解.
2.D
【分析】根据平移的性质得出四边形ABDC是平行四边形,从而得A和C的纵坐标相同,根据四边形ABDC的面积求得AC的长,即可求得C的坐标.
【详解】解:∵把△OAB沿x轴向右平移到△ECD,
∴四边形ABDC是平行四边形,
∴AC=BD,A和C的纵坐标相同,
∵四边形ABDC的面积为9,点A的坐标为(1,3),
∴3AC=9,
∴AC=3,
∴C(4,3),
故选:D.
【点睛】本题考查了坐标与图形的变换-平移,平移的性质,平行四边形的性质,求得平移的距离是解题的关键.
3.A
【分析】分三种情况讨论:①AB为对角线时,②OB为对角线时,③OA为对角线时;分别求出点的坐标,即可得出答案.
【详解】分三种情况:
①AB为对角线时,
∵BM∥OA,点O、A、B的坐标分别是(0,0)(3,0),(1,1),
∴M的坐标为(3+1,1),
即M(4,1);
②OB为对角线时,
∵,点O、A、B的坐标分别是(0,0)(3,0),(1,1),
∴的坐标为(1﹣3,1),
即M(﹣2,1);
③OA为对角线时,点与关于原点O对称,
∴的坐标为(2,﹣1),
即M(2,-1);
综上所述,点M的坐标为(4,1)或(﹣2,1)或(2,﹣1),
故选:A.
【点睛】本题考查了平行四边形的判定与性质、坐标与图形性质以及分类讨论等知识;正确画出图形是解题的关键.
4.B
【分析】分别以AC、AB、BC为对角线画平行四边形,再分别写出个点的坐标,即可选出答案.
【详解】解:如图所示:
①以AC为对角线,可以画出 AFCB,F(-3,1);
②以AB为对角线,可以画出 ACBE,E(5,1);
③以BC为对角线,可以画出 ACDB,D(1,-1);
故选:B.
【点睛】此题主要考查了平行四边形的判定,坐标与图形,关键是分类讨论,正确画出图形.
5.B
【分析】过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,求出△DCN≌△BAE,根据全等三角形的性质得出BE=DN,AE=CN,根据A、B、C的坐标求出OM和DM即可.
【详解】解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
,
∴△DCN≌△BAE(AAS),
∴BE=DN,AE=CN,
∵A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),
∴CN=AE=2﹣1=1,DN=BE=3,
∴DM=3﹣1=2,OM=2+1=3,
∴D的坐标为(3,2),
故选:B.
【点睛】本题考查了全等三角形的性质和判定,平行四边形的性质,点的坐标与图形性质等知识点,能正确作出辅助线是解题的关键.
6.D
【分析】先根据平行四边形的性质和角平分线的作图方法证得AD=DG,结合坐标与图形性质求得OA、OD,再根据勾股定理求得AD即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠DGA=∠BAG,
由作图过程知,AM平分∠DAB,
∴∠DAG=∠BAG,
∴∠DAG=∠DGA,
∴DG=AD,
∵,,
∴OA=6,D(0,8)即OD=8,
∴在Rt△AOD中,AD==10,
∴DG=10,
∴G的坐标为(10,8),
故选:D.
【点睛】本题考查尺规作图-作角平分线、平行四边形的性质、平行线的性质、等角对等边、勾股定理、坐标与图形,熟练掌握相关知识的联系与运用是解答的关键.
7.C
【分析】过点G作GD⊥x轴,根据点的坐标得出AO=,利用平行四边形的性质及角平分线得出∠AOG=∠AGO,由等角对等边得出AO=AG=,结合图形确定GE=,yG=yA=2,即可确定点的坐标.
【详解】解:过点G作GD⊥x轴,同时标注字母如图所示:
∵A(1,2),
∴AO=,
∵四边形AOCB为平行四边形,
∴AB∥OC,
∴∠AGO=∠COG,
∵OF平分∠AOC,
∴∠AOG=∠COG,
∴∠AOG=∠AGO,
∴AO=AG=,
∴GE=,
yG=yA=2,
点G在第二象限,
G(),
故选:C.
【点睛】题目主要考查坐标与图形,平行四边形的性质,勾股定理,角平分线的定义,等角对等边等,理解题意,综合运用这些知识点是解题关键.
8.B
【分析】利用等边三角形的性质可得点D和C的坐标,再利用平行四边形的性质可得P的坐标.
【详解】如图,
以OB、AB为边构造等边△OBD和等边△ABC,
∴∠ODB=∠OBD=60,OB=1,∠CAB=60°,
∴∠OAB=30°,
∴∠OAD=∠DOA=30°,
∴OD=AD=1,
∵点D为AB的中点,
∴AB=2,AO=,
∴,
∴∠CAO=90°,
∴,
∵四边形PBCD是平行四边形,
∴DPBC,DP=BC,
由平移可知,
故选:B.
【点睛】本题主要考查了等边三角形的性质,平行四边形的性质,平移的性质等知识,利用平移的性质得出点P的坐标是解题的关键.
9.D
【分析】过D点作DE⊥BC于点F,根据图像可得平行四边形的边长CD为4,再利用平行四边形的面积可求a.
【详解】如图,当点运动到与点重合时,过点作的垂线,交的延长线于点.
由题意知,当点在上运动时,的面积不变,
此时,.
∵,,
∴,
∴.
【点睛】本题主要考查平行四边形动点问题,函数图像,平行四边形的性质,解题的关键是结合两个图像,随着动点的运动找到对应的函数图像.
10.D
【分析】连接,取中点,连接,根据三角形任意两边之和大于第三边求最值即可.
【详解】解:连接,取中点,连接,
∵,
∴当取最大值时,三点共线,即在之间,
即,
∵分别是的中点,
∴,
∵,
∴,
∴,
∴,
故选:D.
【点睛】本题考查三角形的三边关系,中位线定理,平面直角坐标系中的点与几何,勾股定理,能够熟练掌握数形结合思想是解决本题的关键.
11.(3,2)
【分析】连接AC,BD,两线交于点M,设D点坐标为,利用中点坐标公式即可求解.
【详解】连接AC,BD,两线交于点M,如图,
∵四边形ABCD是平行四边形,
∴对角线AC、BD的交点M为AC、BD的中点,
∵,,,
设D点坐标为,
∴根据中点坐标公式有:,
解得,
∴ D点坐标为,
故答案为:.
【点睛】本题主要考查了平行四边形的性质、中点坐标公式的知识,掌握中点坐标公式是解答本题的关键.
12.(4,﹣3)或(0,9)或(﹣2,﹣3)
【分析】分三种情况:①BC为对角线时,②AB为对角线时,③AC为对角线时,由平行四边形的性质容易得出点D的坐标.
【详解】解:∵A(-1,3),B(2,3),
∴AB=3,轴,
分三种情况:①BC为对角线时, 如图1,
∵四边形ABCD是平行四边形,
∴,AB=CD,
∴轴,
∵AB=3,C(1,-3),
∴点D的坐标为(4,-3)
②AC为对角线时,如图2,
∵四边形ABCD是平行四边形,
∴,AB=CD,
∴轴,
∵AB=3,C(1,﹣3),
∴点D的坐标为(﹣2,﹣3)
③AB为对角线时,如图3,
连接CD交AB于E,
设D的坐标为(x,y),
∵四边形ABCD是平行四边形,
∴E分别为AB、CD的中点,
∵A(-1,3),B(2,3),C(1,-3),
∴,
解得,
∴点D的坐标为(0,9),
综上所述,点D的坐标可能是(4,-3)或(0,9)或(-2,-3).
【点睛】本题考查了平行四边形的性质、坐标与图形的性质;熟练掌握平行四边形的性质是解决问题的关键.
13.(3,4)
【分析】连接OF,延长BC交y轴于点M,则轴,由题意可知,,,.根据平行四边形的性质及作图过程,可知DE垂直平分线段OB,即有,设,则,,然后在中,利用勾股定理可列方程,解得,即,结合图形即可确定F点坐标.
【详解】解:如图,连接OF,延长BC交y轴于点M,则轴,
∵四边形OABC为平行四边形,
∴D为对角线OB中点,
由题意可知,,,,
由作图可知,DE垂直平分线段OB,
∴,
设,则,,
在中,,
即,解得,
∴,
∴点F的坐标为(3,4).
故答案为:(3,4).
【点睛】本题主要考查了平行四边形的性质、图形与坐标、垂直平分线和勾股定理的知识,解题关键是熟练掌握平行四边形的性质.
14.
【分析】先利用平行四边形的性质和角平分线定义得到CO=CD,再设出C点坐标,建立方程即可.
【详解】解:∵四边形OABC是平行四边形,
∴BCOA,
∴∠CDO=∠DOA,
∵OD平分∠COA,
∴∠COD=∠DOA,
∠COD=∠CDO,
∴CO=CD,
∴
设C(m,3),
∴,
解得:,
∴,
故答案为:.
【点睛】本题考查了角平分线的定义和平行四边形的性质,涉及到了勾股定理建立方程的知识,解题关键是正确建立方程并求解,本题蕴含了数形结合的思想.
15.##
【分析】利用勾股定理先求解 再证明 从而可得答案.
【详解】解:∵点A坐标为,
∴
∵,
由作图可得:平分
故答案为:
【点睛】本题考查的是平行四边形的性质,勾股定理的应用,角平分线的作图与计算,等腰三角形的判定,理解题意,证明是解本题的关键.
16.7
【分析】过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E.则由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,即可得出答案.
【详解】解:过点B作BD⊥直线x=6,交直线x=6于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,
直线x=6与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OCAB,OA=BC,
∵直线x=1与直线x=6均垂直于x轴,
∴AMCN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,
,
∴△OAF≌△BCD(ASA).
∴BD=OF=1,
∴OE=6+1=7,
∴
∵OE的长不变,
∴当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=7.
故答案为7.
【点睛】本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质,勾股定理;熟练掌握平行四边形的性质,勾股定理,证明三角形全等是解决问题的关键.
17.##
【分析】设点C坐标为(a,b),由平行四边形的性质可求b=,可得点C在直线y=上运动,再根据点C在y轴上时,AC的长度有最小值求解即可.
【详解】解:设点C坐标为(a,b),
∵顶点B、D分别在x轴和直线y= 3上,
∴点B,点D的纵坐标分别为0, 3,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴,
∴b=,
∴点C在直线y=上运动,
∴当点C在y轴上时,AC的长度有最小值,
∴对角线AC的最小值为:,
故答案为:.
【点睛】本题考查了平行四边形的性质,坐标与图形性质,确定点C的运动轨迹是本题的关键.
18. 10
【分析】由图可知点P在BC上运动时,OP先变小后变大,求出OP的最大值和最小值,过O作于点,则可求得OB=OD= ,OC= ;而从C向D运动时,OP先变小后变大,过点O作于点,利用勾股定理求解即可.
【详解】解:由图可知点P在BC上运动时,OP先变小后变大,
由图象可知:点P从B向C运动时,OP的最大值为,最小值为5,,
∴,
由于M是曲线部分的最低点,
∴此时OP最小,
如下图,过O作于点,,
∴由勾股定理可知:,
∴点M的横坐标为10;
过点O作于点,如下图,
∵四边形ABCD是平行四边形,
∴OD=OB,CD=AB,
由图象可知:点P从C向D运动时,,又,
∴设,则,
∴,
∴,
即,
∴,
∴点N的纵坐标为.
故答案为:10,.
【点睛】本题考查了动点与函数图象的理解和应用、平行四边形的性质、勾股定理.把图形和图象结合理解得到线段长度是解决本题的关键.
19.(1)
(2)
(3)存在,或
【分析】(1)先确定平移的规则,然后根据平移的规则求出点、、的坐标即可;
(2)由平移的性质可知重叠部分为平行四边形且高为2,再根据相似三角形的判定与性质求得底,然后求出面积即可;
(3)设点的坐标为,先求出平行四边形ABCD的面积,然后利用三角形的面积公式即可求出b的值.
【详解】(1)解:∵,,
∴平移的规则为:向右平移2个单位,向上平移一个单位;
∵,,,
∴;
(2)解:如图,延长交x轴于点E,过点做
由平移可知,重叠部分为平行四边形,底边长为3,高为2
∵
即
∴重叠部分的面积为
(3)解:存在;
设点的坐标为,
∵,
,
∴,
∴点的坐标为或.
【点睛】本题主要考查了平移的性质、平行四边形的性质、坐标与图形、求阴影部分的面积等知识点,熟练掌握平移的性质是解题的关键.
20.(1)①见解析;②见解析;
(2).
【分析】(1)①利用平行线的性质和等腰三角形的性质证明即可证明结论;②先根据对称性得到,进而证明,.证明∴.得到,即可证明是等边三角形;
(2)如图所示,过点B作轴于G,过点F作于H,由等边三角形的性质得到,证明四边形是平行四边形,得到,,再由,,证明,得到,利用勾股定理和含30度角的直角三角形的性质求出,则,,同理,据此即可得到答案.
【详解】(1)证明:(1)①∵,
∴.
∵轴,
∴.
∴.
∴平分;
②C是点A关于x轴的对称点,
∴.
∵
∴.
∴.
∴.
在和中
∴.
∴.
∴是等边三角形.
(2)解:如图所示,过点B作轴于G,过点F作于H,
∴,
∵是等边三角形,
∴,
∴,
∵,
∴四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
同理,即,
∴;
【点睛】本题主要考查了坐标与图形,平行线的性质,三角形内角和定理,等边对等角,全等三角形的性质与判定,平行四边形的性质与判定,等边三角形的性质与判定,含30度角的直角三角形的性质,勾股定理等等,灵活运用所学知识是解题的关键.
21.(1)见解析,
(2)见解析
(3)或或
【分析】(1)根据网格结构找出点绕O点逆时针旋转后的对应点的位置,然后顺次连接即可,再根据平面直角坐标系写出点的坐标;
(2)利用关于原点对称的点的坐标特征写出点的对应点的坐标,然后描点即可得到;
(3)根据平行四边形的判定进行求解即可.
【详解】(1)如图,即为所求,点的坐标为.
故答案为:
(2)即为所求;
(3)如图,满足条件的点D的坐标为或或.
故答案为或或.
【点睛】本题考查旋转变换,平行四边形的判定等知识,解题的关键是熟练掌握基本知识.
22.(1)
(2)或
(3)
【分析】(1)利用平行四边形的性质构建方程即可解决问题.
(2)分两种情形:四边形是平行四边形,四边形是等腰梯形,分别求解即可.
(3)利用线段垂直平分线的性质构建方程即可解决问题.
【详解】(1)∵,
∴当时,四边形是平行四边形,
∵,,
∴,
∴
(2)①当四边形是平行四边形时,,
∴,
∴
②当四边形是等腰梯形时,,
此时,
∵,
∴,
∴,
∴
综上,或
(3)∵,
∴.
当垂直平分时,则,
∴,
解得
【点睛】本题考查了平行四边形的判定与性质,等腰梯形,线段垂直平分线的性质,坐标与图形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,利用参数构建方程解决问题.
23.(1)A(4,0),B(0,4)
(2)E(2,)
(3)MH=
【分析】(1)利用非负性求出m、n的值即可得到A、B两点的坐标;
(2)根据AB=BC求出C点坐标,利用平行四边形的性质和中点坐标公式即可求出点E的坐标;
(3)根据等积法和勾股定理求出OH和BH,根据OH和BH求出H点的坐标,再结合M点的坐标即可求出MH的长.
【详解】(1)解:∵
即:
∴
∴ A(4,0),B(0,4)
(2)解:∵OB=OA=4
∴AB=
∴BC=AB=,OC=BC-OB=
C点坐标为(0,)
∵点E是AC中点,
∴,
∴E(2,).
(3)解:∵C与O重合,
∴E为OA的中点,
∴OE=2,
∴BE=,
∵
即:
∴OH=,
∴BH==
设H点的坐标为(x,y)则:
由①-②得:,解得:
把代入①得:或(舍)
∴H
又∵M为AB的中点,
∴M(2,2)
∴MH.
【点睛】本题考查坐标系和几何的综合应用.本题的综合性较强,利用非负性、平行四边形的性质和中点坐标公式,以及勾股定理进行解题.
24.(1)8;
(2)存在,点的坐标为或;
(3)当点在线段的延长线上运动时,; 当点在线段的延长线上运动时,;当点在线段上运动时,.
【分析】(1)根据点的平移规律可得,的坐标,然后利用即可求出四边形的面积;
(2)根据的面积是面积的2倍,得,即可求出点的坐标;
(3)当点在线段延长线上运动时,作,当点在线段的延长线上时,作,当点在线段上运动时,作,分别根据平行线的性质和平行线间的传递性求解即可.
【详解】(1)解:∵点,的坐标分别为、,
∴将点,分别向上平移2个单位长度,再向右平移1个单位长度,得到,的对应点,,
∴,,,,,
∴四边形的面积为:
.
∴点的坐标为,点的坐标为,四边形的面积为.
(2)存在,
如图,设,
∵,,
∴,
又∵的面积是面积的2倍.
∴,
∴,
∵,
∴,
解得:或,
∴点的坐标为或.
(3)当点在线段延长线上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
当点在线段的延长线上时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
当点在线段上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
综上所述:当点在线段的延长线上运动时,;
当点在线段的延长线上运动时,;
当点在线段上运动时,.
【点睛】本题考查平行线的判定和性质,点平移的规律,梯形的面积,三角形的面积等知识点.对点的位置进行分类讨论是解题的关键.
答案第1页,共2页
答案第1页,共2页
