江苏省镇江市润州区镇江实验学校魅力之城分校2023-2024学年上学期八年级数学第一次月考试(无答案)答案)
文档属性
| 名称 | 江苏省镇江市润州区镇江实验学校魅力之城分校2023-2024学年上学期八年级数学第一次月考试(无答案)答案) |  | |
| 格式 | docx | ||
| 文件大小 | 322.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 14:53:26 | ||
图片预览

文档简介
八年级数学第一次限时作业
一、填空题(每空2分,共24分)
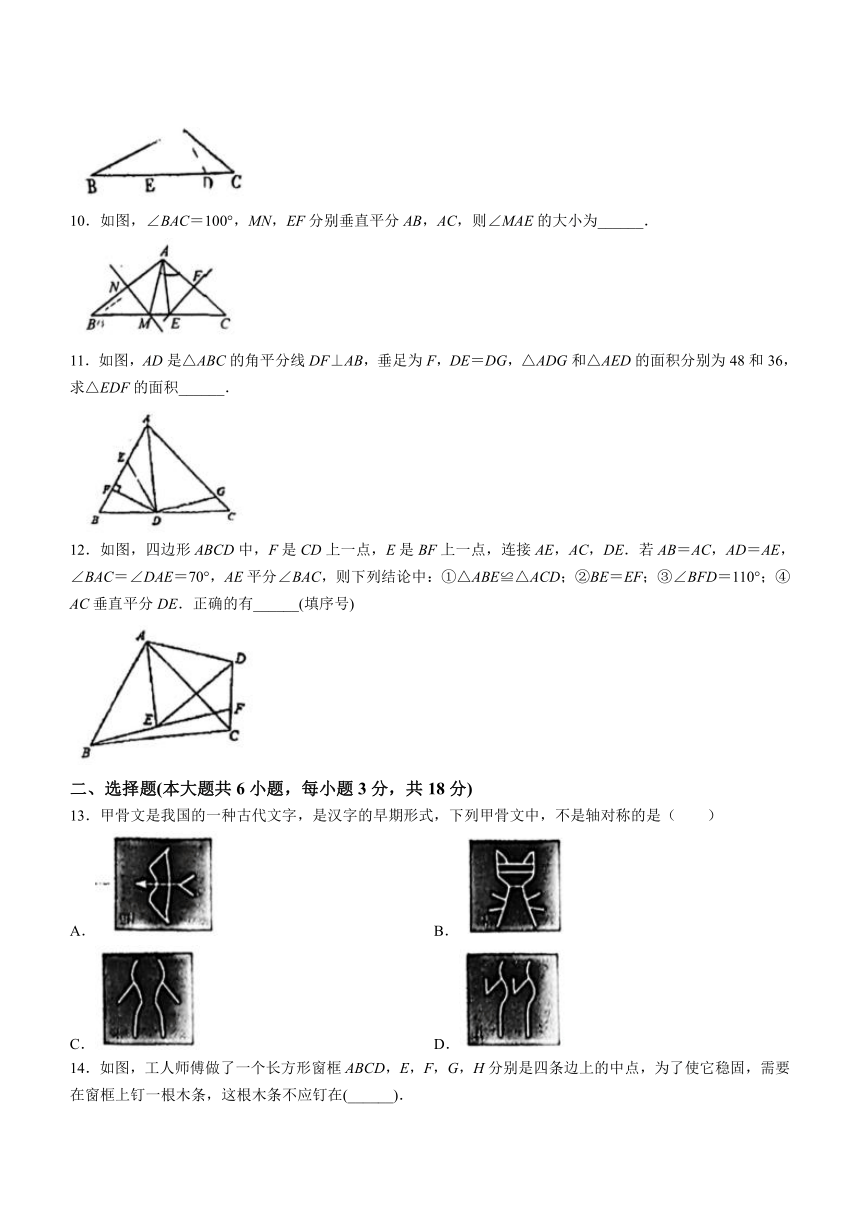
1.如图,△ABC≌△DEF,请根据图中提供的信息,写出x=______.
2.如图,△ABC与关于直线l对称,则∠B的度数为______.
3.如图,已知B,E,F,C在同一直线上,BF=CE,AF=DE,则添加条件______,以判△ABE≌△DCE.
4.等边三角形有______条对称轴.
5.小明从平面镜子中看到镜中电子钟示数的影像如图所示,这时的时刻应是______.
6.已知等腰△ABC的周长是19,AB=7,则BC=______.
7.等腰三角形的一个外角为70°,则它的底角为______.
8.如图,∠AOB内有一点P,∠AOB=35°,点M、N分别是射线OB、OA上的动点.当△PMN的周长最小时,∠MPN的度数是______.
9.如图,已知△ABC中,点D、E在BC上,且AC=AE=BE=ED,∠DAC=27°,则∠B=______°.
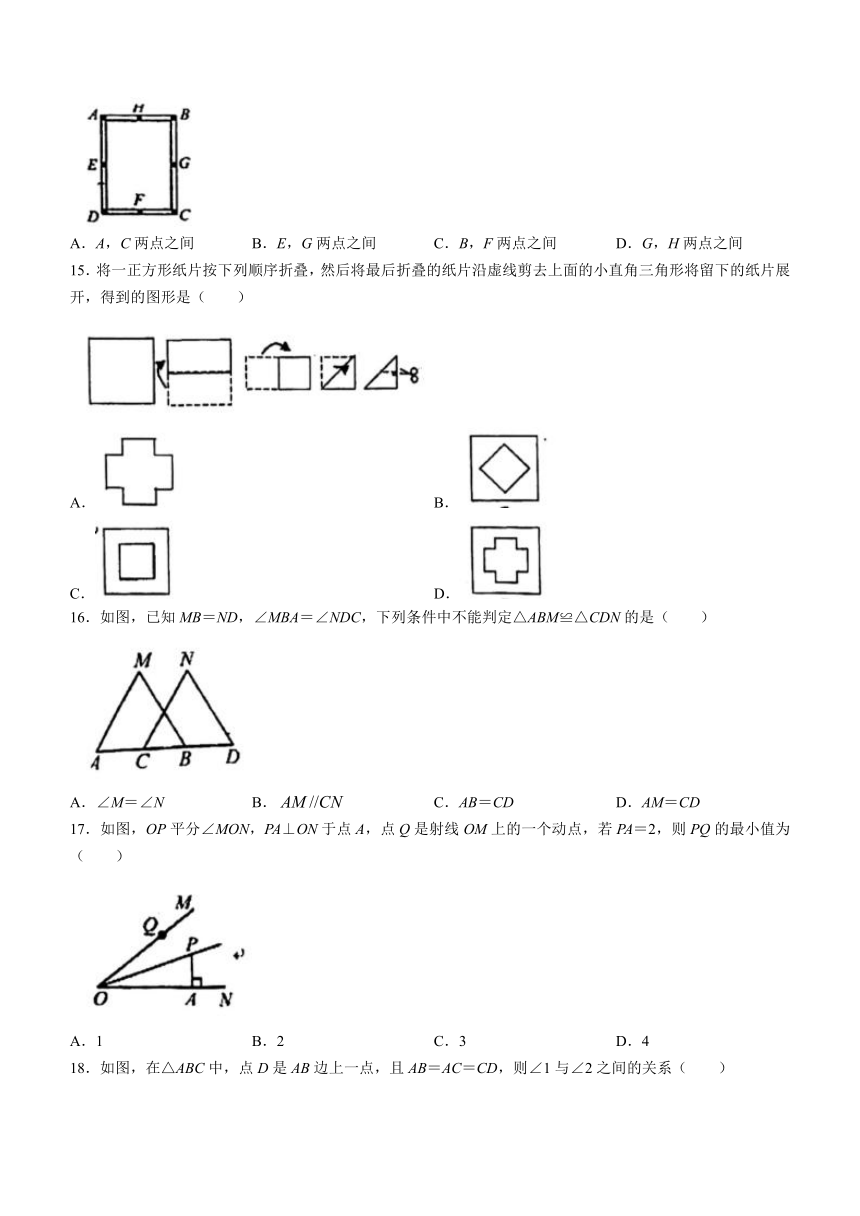
10.如图,∠BAC=100°,MN,EF分别垂直平分AB,AC,则∠MAE的大小为______.
11.如图,AD是△ABC的角平分线DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积______.
12.如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE,AC,DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD;②BE=EF;③∠BFD=110°;④AC垂直平分DE.正确的有______(填序号)
二、选择题(本大题共6小题,每小题3分,共18分)
13.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )
A. B.
C. D.
14.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(______).
A.A,C两点之间 B.E,G两点之间 C.B,F两点之间 D.G,H两点之间
15.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的小直角三角形将留下的纸片展开,得到的图形是( )
A. B.
C. D.
16.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B. C.AB=CD D.AM=CD
17.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
A.1 B.2 C.3 D.4
18.如图,在△ABC中,点D是AB边上一点,且AB=AC=CD,则∠1与∠2之间的关系( )
A.3∠2﹣2∠1=180° B.2∠2+∠1=180° C.3∠2﹣∠1=180° D.∠1=2∠2
三、解答题(共78分)
19.如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的;
(2)三角形ABC的面积为______;
(3)在直线l上找一点P,使PB+PC的长最短
20.某国际帆船中心外形形状是一个三角形,要在它的内部修建一处公共服务设施(用点P表示),使它到公路AB、BC的距离相等,且到点B、C的距离也相等.在图中确定公共服务设施P的位置.(不写作法,保留作图痕迹)
21.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.
22.如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
23.已知:如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分为E、F
求证:(1)BE=CF;
(2)连结EF,则直线AD与线段EF有何位置关系 为什么
24.如图,在△ABC中,AB=AC,点O在高AE上,且OA=OB,连接BO并延长交AC于点D.
(1)求证:∠BAC=2∠ABD
(2)若△BCD是等腰三角形,求∠BAC的度数。
25.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A,B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P,Q运动到某处时,有△ACP与△BPQ全等,求出相应的x,t的值.
图(1) 图(2)
26.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=______°.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系 请说明理由;
②当点D在直线BC上移动,则α、β之间有怎样的数量关系 请画出图形,并直接写出你的结论.
图1 图1 备用图
一、填空题(每空2分,共24分)
1.如图,△ABC≌△DEF,请根据图中提供的信息,写出x=______.
2.如图,△ABC与关于直线l对称,则∠B的度数为______.
3.如图,已知B,E,F,C在同一直线上,BF=CE,AF=DE,则添加条件______,以判△ABE≌△DCE.
4.等边三角形有______条对称轴.
5.小明从平面镜子中看到镜中电子钟示数的影像如图所示,这时的时刻应是______.
6.已知等腰△ABC的周长是19,AB=7,则BC=______.
7.等腰三角形的一个外角为70°,则它的底角为______.
8.如图,∠AOB内有一点P,∠AOB=35°,点M、N分别是射线OB、OA上的动点.当△PMN的周长最小时,∠MPN的度数是______.
9.如图,已知△ABC中,点D、E在BC上,且AC=AE=BE=ED,∠DAC=27°,则∠B=______°.
10.如图,∠BAC=100°,MN,EF分别垂直平分AB,AC,则∠MAE的大小为______.
11.如图,AD是△ABC的角平分线DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积______.
12.如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE,AC,DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD;②BE=EF;③∠BFD=110°;④AC垂直平分DE.正确的有______(填序号)
二、选择题(本大题共6小题,每小题3分,共18分)
13.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )
A. B.
C. D.
14.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(______).
A.A,C两点之间 B.E,G两点之间 C.B,F两点之间 D.G,H两点之间
15.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的小直角三角形将留下的纸片展开,得到的图形是( )
A. B.
C. D.
16.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B. C.AB=CD D.AM=CD
17.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
A.1 B.2 C.3 D.4
18.如图,在△ABC中,点D是AB边上一点,且AB=AC=CD,则∠1与∠2之间的关系( )
A.3∠2﹣2∠1=180° B.2∠2+∠1=180° C.3∠2﹣∠1=180° D.∠1=2∠2
三、解答题(共78分)
19.如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的;
(2)三角形ABC的面积为______;
(3)在直线l上找一点P,使PB+PC的长最短
20.某国际帆船中心外形形状是一个三角形,要在它的内部修建一处公共服务设施(用点P表示),使它到公路AB、BC的距离相等,且到点B、C的距离也相等.在图中确定公共服务设施P的位置.(不写作法,保留作图痕迹)
21.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.
22.如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
23.已知:如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分为E、F
求证:(1)BE=CF;
(2)连结EF,则直线AD与线段EF有何位置关系 为什么
24.如图,在△ABC中,AB=AC,点O在高AE上,且OA=OB,连接BO并延长交AC于点D.
(1)求证:∠BAC=2∠ABD
(2)若△BCD是等腰三角形,求∠BAC的度数。
25.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A,B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P,Q运动到某处时,有△ACP与△BPQ全等,求出相应的x,t的值.
图(1) 图(2)
26.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=______°.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系 请说明理由;
②当点D在直线BC上移动,则α、β之间有怎样的数量关系 请画出图形,并直接写出你的结论.
图1 图1 备用图
同课章节目录
