河南省南阳市方城县2023-2024学年八年级上学期第一次质量评估数学试题(含答案)
文档属性
| 名称 | 河南省南阳市方城县2023-2024学年八年级上学期第一次质量评估数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 560.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 00:00:00 | ||
图片预览



文档简介
2023–2024学年度第一学期阶段性测试卷(1/4)
八年级数学(HS)
测试范围:11.1-12.3
注意事项:
1.本试卷共6页,三大题,满分120分,测试时间100分钟。
2.请用蓝、黑色钢笔或圆珠笔写在试卷或答题卡上。
3.答卷前请将密封线内的项目填写清楚。
一、选择题(每小题3分,共30分)
1.下列实数中无理数是( )
A.-2 B.0 C. D.
2.若一个数的算术平方根是8,则这个数的立方根是( )
A. B. C.2 D.4
3.下列运算不正确的是( )
A. B. C. D.
4.如果的乘积中不含的一次项,则为( )
A.4 B.-4 C.2 D.-2
5.下列说法正确的有( )
①实数与数轴上的点一一对应;②负数没有立方根;③16的平方根是4;④的相反数是.
A.2个 B.3个 C.4个 D.1个
6.下列各数,立方根一定是负数的是( )
A. B. C. D.
7.下列式子不能用平方差公式计算的是( )
A. B.
C. D.
8.若为实数,在“□”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则不可能是( )
A. B. C. D.
9.在边长为的正方形中挖去一个边长为的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A. B.
C. D.
10.已知表示取三个数中最小的那个数.例如:,当时,则的值为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.写出一个比3大且比4小的无理数:______.
12.计算:=______.
13.已知关于的多项式是一个完全平方式,则=______.
14.如图,点在数轴上,点表示的数是-1,点是的中点,线段,则点表示的数是______.
第14题图
15.如图,长方形的边,是边上的一点,且,分别是线段上的动点,且,现以为边作长方形,以为边作正方形,点均在长方形内部.记图中的阴影部分面积分别为,长方形和正方形的重叠部分是四边形,当四边形的邻边比为3:4时,的值为______.
第15题图
三、解答题(共8题,共75分)
16.(12分)(1);
(2);
(3);
(4).
17.(12分)(1)计算:;
(2)计算:;
(3)用简便方法计算:;
(4)先化简,再求值:,其中,.
18.(8分)已知:实数满足,
(1)求;
(2)当一个正实数的两个平方根分别为和时,求的值.
19.(8分)已知,,求下列各式的值.
(1);
(2).
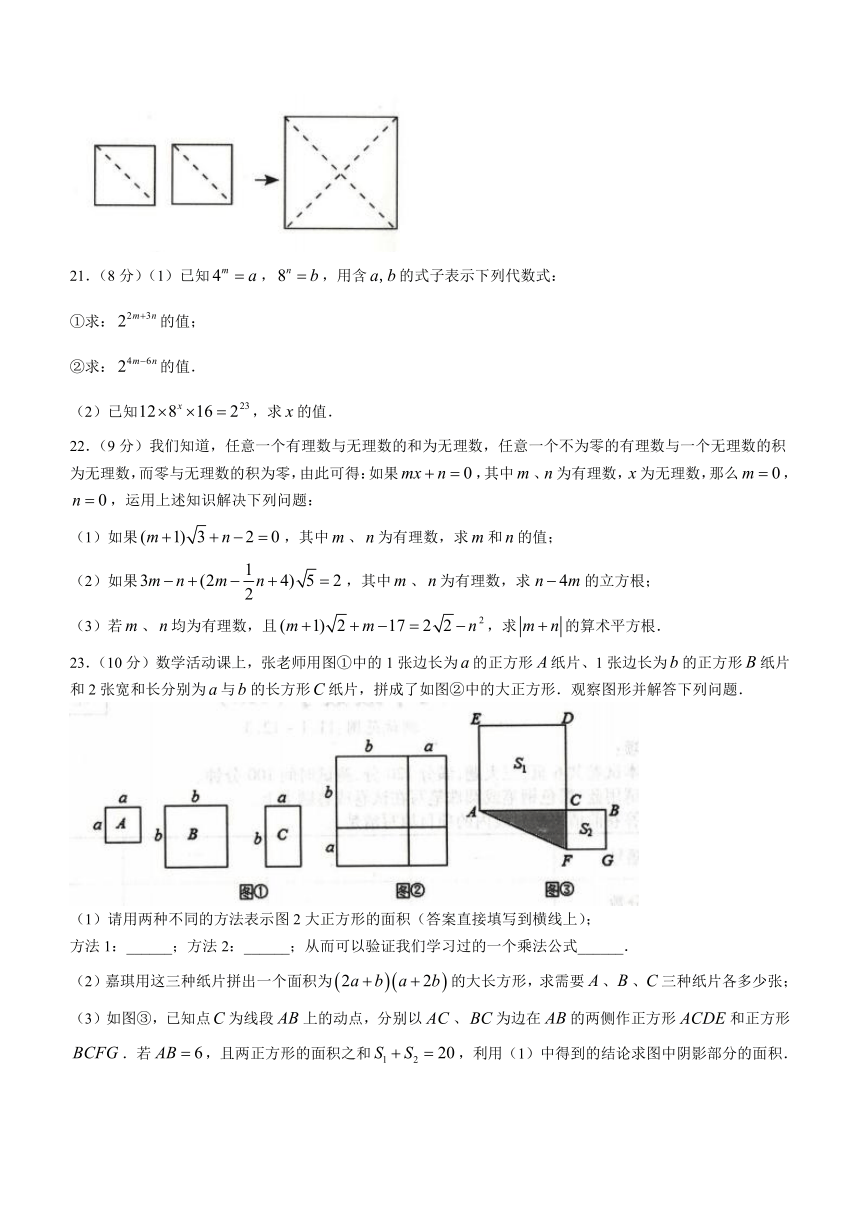
20.(8分)【综合与实践】如图,把两个面积均为的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.
(1)求大正方形纸片的边长;
(2)若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为3:1,且面积为?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.
21.(8分)(1)已知,,用含的式子表示下列代数式:
①求:的值;
②求:的值.
(2)已知,求的值.
22.(9分)我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零,由此可得:如果,其中、为有理数,为无理数,那么,,运用上述知识解决下列问题:
(1)如果,其中、为有理数,求和的值;
(2)如果,其中、为有理数,求的立方根;
(3)若、均为有理数,且,求的算术平方根.
23.(10分)数学活动课上,张老师用图①中的1张边长为的正方形纸片、1张边长为的正方形纸片和2张宽和长分别为与的长方形纸片,拼成了如图②中的大正方形.观察图形并解答下列问题.
(1)请用两种不同的方法表示图2大正方形的面积(答案直接填写到横线上);
方法1:______;方法2:______;从而可以验证我们学习过的一个乘法公式______.
(2)嘉琪用这三种纸片拼出一个面积为的大长方形,求需要、、三种纸片各多少张;
(3)如图③,已知点为线段上的动点,分别以、为边在的两侧作正方形和正方形.若,且两正方形的面积之和,利用(1)中得到的结论求图中阴影部分的面积.
2023–2024学年度第一学期阶段性测试卷(1/4)参考答案
八年级数学(HS)
一、选择题(每小题3分,共30分)
1.D 2.D 3.A 4.B 5.A 6.B 7.B 8.C 9.C 10.A
二、填空题(每小题3分,共15分)
11.(答案不唯一) 12. 13.9 14. 15.7或
三、解答题(共8题,共75分)
16.解:(1)原式;
(2)原式;
(3),
,
,
或,
或;
(4),
,
,
或,
或,
17.解:(1)原式;
(2)原式;
(3)原式;
(4)原式,
当时,时,原式.
18.解:(1)∵,∴,
∴,,
∴,
∴的值为-1;
(2)∵一个正实数的两个平方根分别为和,
∴,
∴,
解得:,
∴,
∴的值为100.
19.解:已知,,
(1);
(2).
20.解:(1)由题意得:大正方形的面积,
∴大正方形纸片的边长.
(2)沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片,理由如下:
∵长方形纸片的长宽之比为3:1,
∴设长方形纸片的长和宽分别是,,
∴,
∴,
∵,∴,∴长方形纸片的长是,
∵,
∴沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片.
21.解:(1)∵,,
∴,,
;
;
(2)∵,
∴,
∴,
∴,
解得:
22.解:(1)如果,其中、为有理数,
根据,其中、为有理数,为无理数,那么,,
则,,
则,,
(2)如果,其中、为有理数,
根据,其中、为有理数,为无理数,那么,,
则,,
解得:,,
,
,
的立方根为:2
(3)、均为有理数,且,
根据,其中、为有理数,为无理数,那么,,
则,,
解得,,
当,时,,
当,时,,
故的算术平方根为:或
23.解:(1),,.
(2)∵,∴所需、两种纸片各2张,种纸片5张.
(3)设,则,
∵,
∴
∵,
∴,
∴,∴,
∴.
八年级数学(HS)
测试范围:11.1-12.3
注意事项:
1.本试卷共6页,三大题,满分120分,测试时间100分钟。
2.请用蓝、黑色钢笔或圆珠笔写在试卷或答题卡上。
3.答卷前请将密封线内的项目填写清楚。
一、选择题(每小题3分,共30分)
1.下列实数中无理数是( )
A.-2 B.0 C. D.
2.若一个数的算术平方根是8,则这个数的立方根是( )
A. B. C.2 D.4
3.下列运算不正确的是( )
A. B. C. D.
4.如果的乘积中不含的一次项,则为( )
A.4 B.-4 C.2 D.-2
5.下列说法正确的有( )
①实数与数轴上的点一一对应;②负数没有立方根;③16的平方根是4;④的相反数是.
A.2个 B.3个 C.4个 D.1个
6.下列各数,立方根一定是负数的是( )
A. B. C. D.
7.下列式子不能用平方差公式计算的是( )
A. B.
C. D.
8.若为实数,在“□”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则不可能是( )
A. B. C. D.
9.在边长为的正方形中挖去一个边长为的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A. B.
C. D.
10.已知表示取三个数中最小的那个数.例如:,当时,则的值为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.写出一个比3大且比4小的无理数:______.
12.计算:=______.
13.已知关于的多项式是一个完全平方式,则=______.
14.如图,点在数轴上,点表示的数是-1,点是的中点,线段,则点表示的数是______.
第14题图
15.如图,长方形的边,是边上的一点,且,分别是线段上的动点,且,现以为边作长方形,以为边作正方形,点均在长方形内部.记图中的阴影部分面积分别为,长方形和正方形的重叠部分是四边形,当四边形的邻边比为3:4时,的值为______.
第15题图
三、解答题(共8题,共75分)
16.(12分)(1);
(2);
(3);
(4).
17.(12分)(1)计算:;
(2)计算:;
(3)用简便方法计算:;
(4)先化简,再求值:,其中,.
18.(8分)已知:实数满足,
(1)求;
(2)当一个正实数的两个平方根分别为和时,求的值.
19.(8分)已知,,求下列各式的值.
(1);
(2).
20.(8分)【综合与实践】如图,把两个面积均为的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.
(1)求大正方形纸片的边长;
(2)若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为3:1,且面积为?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.
21.(8分)(1)已知,,用含的式子表示下列代数式:
①求:的值;
②求:的值.
(2)已知,求的值.
22.(9分)我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零,由此可得:如果,其中、为有理数,为无理数,那么,,运用上述知识解决下列问题:
(1)如果,其中、为有理数,求和的值;
(2)如果,其中、为有理数,求的立方根;
(3)若、均为有理数,且,求的算术平方根.
23.(10分)数学活动课上,张老师用图①中的1张边长为的正方形纸片、1张边长为的正方形纸片和2张宽和长分别为与的长方形纸片,拼成了如图②中的大正方形.观察图形并解答下列问题.
(1)请用两种不同的方法表示图2大正方形的面积(答案直接填写到横线上);
方法1:______;方法2:______;从而可以验证我们学习过的一个乘法公式______.
(2)嘉琪用这三种纸片拼出一个面积为的大长方形,求需要、、三种纸片各多少张;
(3)如图③,已知点为线段上的动点,分别以、为边在的两侧作正方形和正方形.若,且两正方形的面积之和,利用(1)中得到的结论求图中阴影部分的面积.
2023–2024学年度第一学期阶段性测试卷(1/4)参考答案
八年级数学(HS)
一、选择题(每小题3分,共30分)
1.D 2.D 3.A 4.B 5.A 6.B 7.B 8.C 9.C 10.A
二、填空题(每小题3分,共15分)
11.(答案不唯一) 12. 13.9 14. 15.7或
三、解答题(共8题,共75分)
16.解:(1)原式;
(2)原式;
(3),
,
,
或,
或;
(4),
,
,
或,
或,
17.解:(1)原式;
(2)原式;
(3)原式;
(4)原式,
当时,时,原式.
18.解:(1)∵,∴,
∴,,
∴,
∴的值为-1;
(2)∵一个正实数的两个平方根分别为和,
∴,
∴,
解得:,
∴,
∴的值为100.
19.解:已知,,
(1);
(2).
20.解:(1)由题意得:大正方形的面积,
∴大正方形纸片的边长.
(2)沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片,理由如下:
∵长方形纸片的长宽之比为3:1,
∴设长方形纸片的长和宽分别是,,
∴,
∴,
∵,∴,∴长方形纸片的长是,
∵,
∴沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片.
21.解:(1)∵,,
∴,,
;
;
(2)∵,
∴,
∴,
∴,
解得:
22.解:(1)如果,其中、为有理数,
根据,其中、为有理数,为无理数,那么,,
则,,
则,,
(2)如果,其中、为有理数,
根据,其中、为有理数,为无理数,那么,,
则,,
解得:,,
,
,
的立方根为:2
(3)、均为有理数,且,
根据,其中、为有理数,为无理数,那么,,
则,,
解得,,
当,时,,
当,时,,
故的算术平方根为:或
23.解:(1),,.
(2)∵,∴所需、两种纸片各2张,种纸片5张.
(3)设,则,
∵,
∴
∵,
∴,
∴,∴,
∴.
同课章节目录
