12.2三角形全等的判定 同步练习(含答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 12.2三角形全等的判定 同步练习(含答案) 2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 15:36:00 | ||
图片预览


文档简介
12.2三角形全等的判定
一、选择题
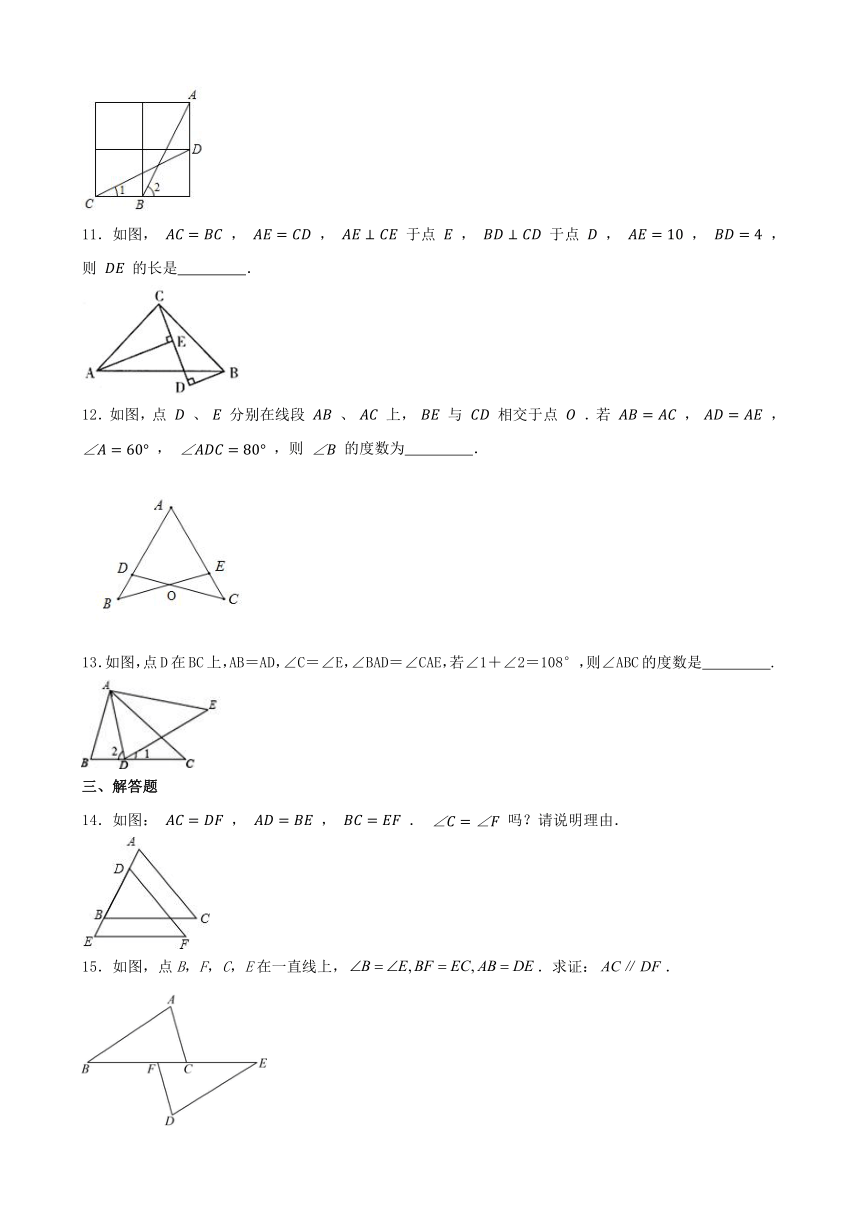
1.如图,,,添加下列一个条件后,不能使的是( )
A. B. C. D.
2.如图,要测量中心湖两岸相对两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再在BF的垂线DG上取点E,使点A,C,E在一条直线上,可得△ABC≌△EDC.判定全等的依据是( )
A.SSS B.SAS C.ASA D.HL
3.如图,在ABC中,AB=AC,AD⊥BC于点D,则下列结论,一定成立的是( )
A.BD=AD B.∠B=∠C
C.AD=CD D.∠BAD=∠ACD
4.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOC等于( )
A. B. C. D.
5.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚可以放进一个等腰直角三角板(AC=BC, ∠ACB=90°)点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为( )
A.10cm B.14cm C.20cm D.6cm
6.如图,在中,,则的度数为( )
A. B. C. D.
7.如图,已知△ABC的面积为12,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是( )
A.10 B.8 C.6 D.4
8.如图,已知,,过点A,且,,垂足分别为点,,则的长为( )
A.8 B.6 C.4 D.求不出来
二、填空题
9.如图,在 和 中, , ,当添加条件 时,就可得到 .(只需填写一个你认为正确的条件)
10.如图,在2×2的正方形网格中,线段AB、CD的端点均在格点上,则∠1+∠2= °.
11.如图, , , 于点 , 于点 , , ,则 的长是 .
12.如图,点 、 分别在线段 、 上, 与 相交于点 .若 , , , ,则 的度数为 .
13.如图,点D在BC上,AB=AD,∠C=∠E,∠BAD=∠CAE,若∠1+∠2=108°,则∠ABC的度数是 .
三、解答题
14.如图: , , . 吗?请说明理由.
15.如图,点B,F,C,E在一直线上,.求证:.
16.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
17.如图,在中,点D是上一点,且,,,连接交于点F.
(1)若,求的度数;
(2)若平分,求证:.
18.如图,交于点B,,.
(1)求证:;
(2)若,求的度数.
参考答案
1.B
2.C
3.B
4.B
5.C
6.C
7.C
8.A
9.AC=DE(或∠ABC=∠DFE,答案不唯一).
10.90°
11.6
12.40°
13.72°
14.解:∵ ,
∴ ,
即 ,
又∵ , ,
∴ ≌ ,
∴ .
15.证明:∵,
∴,
∴,
在和中,,
∴,
∴,
∴.
16.证明:∵点E,F在BC上,BE=CF,
∴BE+EF=CF+EF,即BF=CE;
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=CD(全等三角形的对应边相等).
17.(1)解:,,,
,
又,
.
(2)证明:平分,
,
,
,
又,
,即:,
在和中,
,
.
18.(1)证明:∵,
∴,
∵,.
∴,
∴.
(2)解:∵,,
∴,
∵,
∴,
∵,
∴
一、选择题
1.如图,,,添加下列一个条件后,不能使的是( )
A. B. C. D.
2.如图,要测量中心湖两岸相对两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再在BF的垂线DG上取点E,使点A,C,E在一条直线上,可得△ABC≌△EDC.判定全等的依据是( )
A.SSS B.SAS C.ASA D.HL
3.如图,在ABC中,AB=AC,AD⊥BC于点D,则下列结论,一定成立的是( )
A.BD=AD B.∠B=∠C
C.AD=CD D.∠BAD=∠ACD
4.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOC等于( )
A. B. C. D.
5.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚可以放进一个等腰直角三角板(AC=BC, ∠ACB=90°)点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为( )
A.10cm B.14cm C.20cm D.6cm
6.如图,在中,,则的度数为( )
A. B. C. D.
7.如图,已知△ABC的面积为12,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是( )
A.10 B.8 C.6 D.4
8.如图,已知,,过点A,且,,垂足分别为点,,则的长为( )
A.8 B.6 C.4 D.求不出来
二、填空题
9.如图,在 和 中, , ,当添加条件 时,就可得到 .(只需填写一个你认为正确的条件)
10.如图,在2×2的正方形网格中,线段AB、CD的端点均在格点上,则∠1+∠2= °.
11.如图, , , 于点 , 于点 , , ,则 的长是 .
12.如图,点 、 分别在线段 、 上, 与 相交于点 .若 , , , ,则 的度数为 .
13.如图,点D在BC上,AB=AD,∠C=∠E,∠BAD=∠CAE,若∠1+∠2=108°,则∠ABC的度数是 .
三、解答题
14.如图: , , . 吗?请说明理由.
15.如图,点B,F,C,E在一直线上,.求证:.
16.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
17.如图,在中,点D是上一点,且,,,连接交于点F.
(1)若,求的度数;
(2)若平分,求证:.
18.如图,交于点B,,.
(1)求证:;
(2)若,求的度数.
参考答案
1.B
2.C
3.B
4.B
5.C
6.C
7.C
8.A
9.AC=DE(或∠ABC=∠DFE,答案不唯一).
10.90°
11.6
12.40°
13.72°
14.解:∵ ,
∴ ,
即 ,
又∵ , ,
∴ ≌ ,
∴ .
15.证明:∵,
∴,
∴,
在和中,,
∴,
∴,
∴.
16.证明:∵点E,F在BC上,BE=CF,
∴BE+EF=CF+EF,即BF=CE;
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=CD(全等三角形的对应边相等).
17.(1)解:,,,
,
又,
.
(2)证明:平分,
,
,
,
又,
,即:,
在和中,
,
.
18.(1)证明:∵,
∴,
∵,.
∴,
∴.
(2)解:∵,,
∴,
∵,
∴,
∵,
∴
