13.4课题学习最短路径同步练习(含答案)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 13.4课题学习最短路径同步练习(含答案)2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
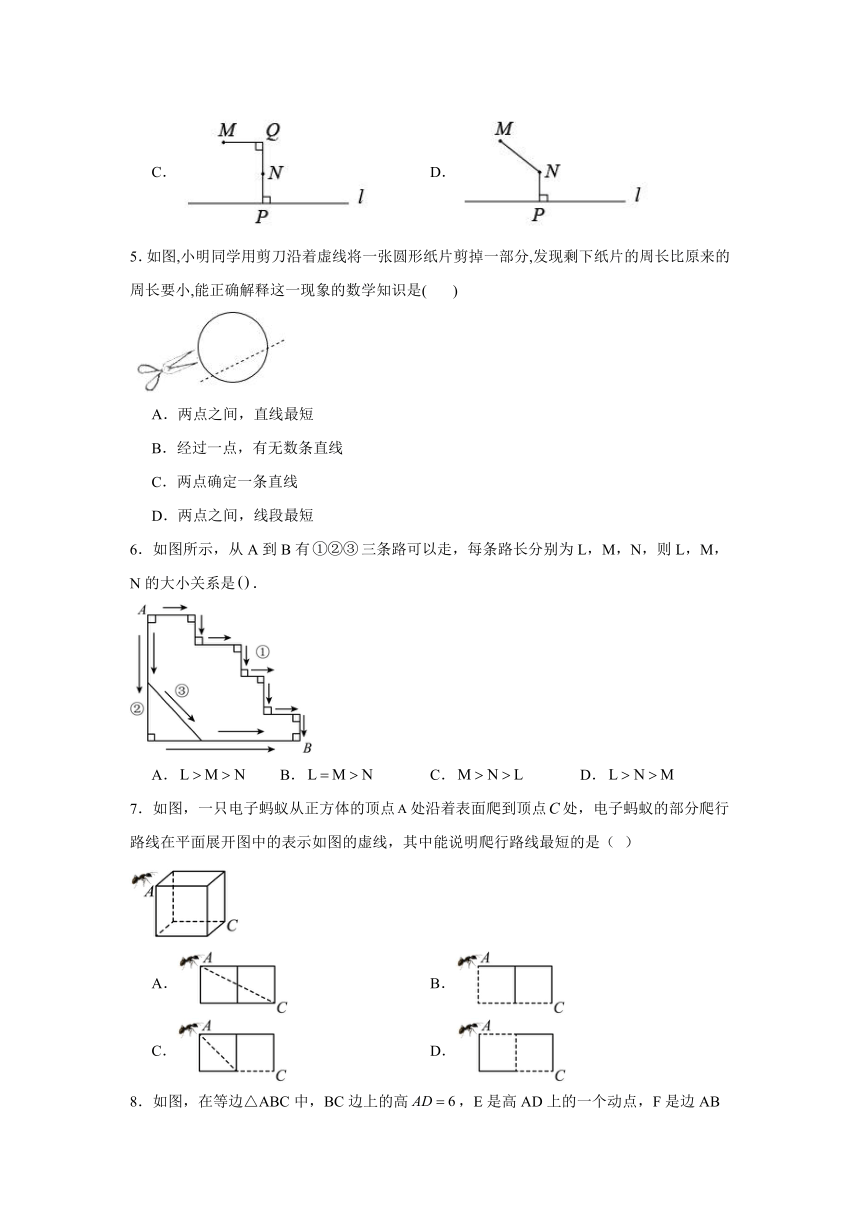
| 文件大小 | 566.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
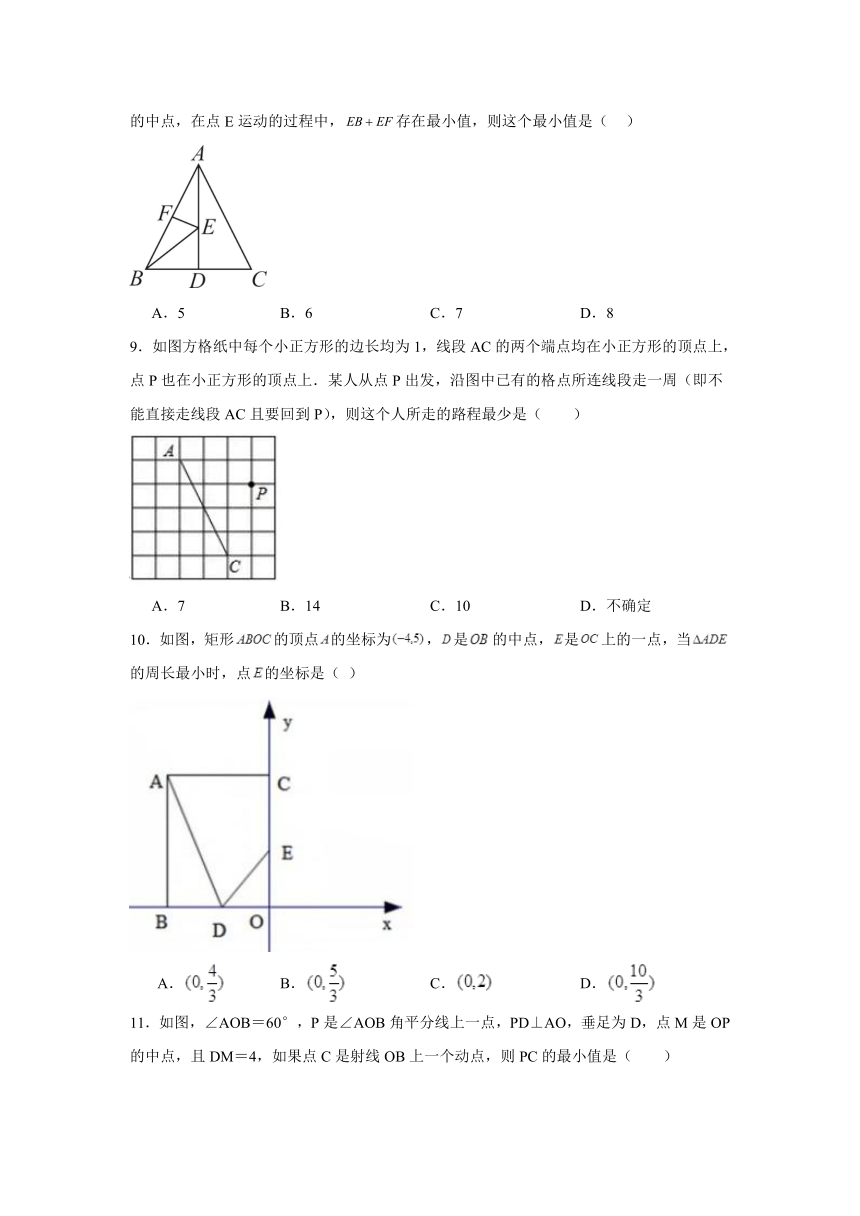
| 更新时间 | 2023-10-26 15:40:51 | ||
图片预览



文档简介
13.4 课题学习 最短路径 同步练习
一、单选题
1.如图,从A到B最短的路线是( )
A. B.
C. D.
2.已知点M(-4,2),若点N是y轴上一动点,则M,N两点之间的距离最小值为( )
A.-4 B.2 C.4 D.-2
3.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
4.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A. B.
C. D.
5.如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短
B.经过一点,有无数条直线
C.两点确定一条直线
D.两点之间,线段最短
6.如图所示,从A到B有三条路可以走,每条路长分别为L,M,N,则L,M,N的大小关系是.
A. B. C. D.
7.如图,一只电子蚂蚁从正方体的顶点处沿着表面爬到顶点处,电子蚂蚁的部分爬行路线在平面展开图中的表示如图的虚线,其中能说明爬行路线最短的是( )
A. B.
C. D.
8.如图,在等边△ABC中,BC边上的高,E是高AD上的一个动点,F是边AB
的中点,在点E运动的过程中,存在最小值,则这个最小值是( )
A.5 B.6 C.7 D.8
9.如图方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上,点P也在小正方形的顶点上.某人从点P出发,沿图中已有的格点所连线段走一周(即不能直接走线段AC且要回到P),则这个人所走的路程最少是( )
A.7 B.14 C.10 D.不确定
10.如图,矩形的顶点的坐标为,是的中点,是上的一点,当的周长最小时,点的坐标是( )
A. B. C. D.
11.如图,∠AOB=60°,P是∠AOB角平分线上一点,PD⊥AO,垂足为D,点M是OP的中点,且DM=4,如果点C是射线OB上一个动点,则PC的最小值是( )
A.8 B.6 C.4 D.2
12.如图,某工厂有三个住宅区,A、B、C各区分别住有职工15人、20人、45人,且这三个区在一条大道上(A、B、C三点共线),已知AB=1500m,BC=1000m,为了方便职工上下班,该工厂打算从以下四处中选一处设置接送车停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.A住宅区 B.B住宅区
C.C住宅区 D.B、C住宅区中间D处
二、填空题
13.如图,是一条笔直的公路,在公路的两侧各有一个村庄,,两个村庄准备集资修建一个公交车站,经过协商,要求车站到两个村庄的路程和最短,小聪帮助设计了公交车站修建点,则小聪设计的理由是 .
14.如图所示,在边长为4的正方形中,、分别为、的中点,为对角线上的一个动点,则的最小值的是 .
15.如图,,点M,N分别是边,上的定点,点P,Q分别是边,上的动点,记,,当最小时,则α与β的数量关系为 .
16.如图,,,分别为射线,上的动点,为内一点,连接,,.若,则周长的最小值为 .
17.如图,,点P为内一点,.点M、N分别在上.当△PMN周长最小时,下列结论:①等于;②等于;③等于;④△PMN周长最小值是5:⑤△PMN周长最小值是10;⑥△PMN周长最小值是15.其中正确结论的序号是 .
三、解答题
18.作图题:(不需证明,只保留作图痕迹)、是两个村庄,、 是一条河流的两岸.
(1)在河岸建立水站,使,试确定点的位置.
(2)在河岸上建立水站,若使管道最短,确定点的位置.
19.如图,在锐角中,,,平分,分别是和上的动点,求的最小值并说明理由.
20.如图,在平面直角坐标系中,△ABC三个顶点的坐标为、、.
(1)在图中作出△ABC关于轴的对称图形△;
(2)请直接写出点的坐标___________;
(3)在轴上画出一点使的值最小.
21.如图,已知点A,B,C,D是不在同一直线上的四个点,请按要求画出图形.
(1)作线段和射线;
(2)用无刻度的直尺和圆规在射线上作;
(3)在平面内作一点P,使得的和最短.
参考答案:
1.C
2.C
3.D
4.D
5.D
6.B
7.A
8.B
9.B
10.B
11.C
12.C
13.两点之间线段最短
14.
15.
16.5
17.①⑤/⑤①
18.(1)如图所示,点为所找到的位置.
(2)如图所示,点为所找到的位置.
19.
20.解:(1)根据题意得:点、、关于轴的对称的的对应点分别为、、,画出图形,如图所示:
(2)点的坐标为;
(3)如图,作点关于 轴的对称点 ,连接 交 轴于点 ,则点即为所求,
∵点 与 关于轴对称,
∴ ,
∴,
即当点 三点共线时,的值最小.
21.(1)解:如图:
(2)解:如图:
(3)解:点P即为所求.
两点之间线段最短,
要使得的和最短,则点应为线段和线段的交点.
一、单选题
1.如图,从A到B最短的路线是( )
A. B.
C. D.
2.已知点M(-4,2),若点N是y轴上一动点,则M,N两点之间的距离最小值为( )
A.-4 B.2 C.4 D.-2
3.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
4.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A. B.
C. D.
5.如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短
B.经过一点,有无数条直线
C.两点确定一条直线
D.两点之间,线段最短
6.如图所示,从A到B有三条路可以走,每条路长分别为L,M,N,则L,M,N的大小关系是.
A. B. C. D.
7.如图,一只电子蚂蚁从正方体的顶点处沿着表面爬到顶点处,电子蚂蚁的部分爬行路线在平面展开图中的表示如图的虚线,其中能说明爬行路线最短的是( )
A. B.
C. D.
8.如图,在等边△ABC中,BC边上的高,E是高AD上的一个动点,F是边AB
的中点,在点E运动的过程中,存在最小值,则这个最小值是( )
A.5 B.6 C.7 D.8
9.如图方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上,点P也在小正方形的顶点上.某人从点P出发,沿图中已有的格点所连线段走一周(即不能直接走线段AC且要回到P),则这个人所走的路程最少是( )
A.7 B.14 C.10 D.不确定
10.如图,矩形的顶点的坐标为,是的中点,是上的一点,当的周长最小时,点的坐标是( )
A. B. C. D.
11.如图,∠AOB=60°,P是∠AOB角平分线上一点,PD⊥AO,垂足为D,点M是OP的中点,且DM=4,如果点C是射线OB上一个动点,则PC的最小值是( )
A.8 B.6 C.4 D.2
12.如图,某工厂有三个住宅区,A、B、C各区分别住有职工15人、20人、45人,且这三个区在一条大道上(A、B、C三点共线),已知AB=1500m,BC=1000m,为了方便职工上下班,该工厂打算从以下四处中选一处设置接送车停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.A住宅区 B.B住宅区
C.C住宅区 D.B、C住宅区中间D处
二、填空题
13.如图,是一条笔直的公路,在公路的两侧各有一个村庄,,两个村庄准备集资修建一个公交车站,经过协商,要求车站到两个村庄的路程和最短,小聪帮助设计了公交车站修建点,则小聪设计的理由是 .
14.如图所示,在边长为4的正方形中,、分别为、的中点,为对角线上的一个动点,则的最小值的是 .
15.如图,,点M,N分别是边,上的定点,点P,Q分别是边,上的动点,记,,当最小时,则α与β的数量关系为 .
16.如图,,,分别为射线,上的动点,为内一点,连接,,.若,则周长的最小值为 .
17.如图,,点P为内一点,.点M、N分别在上.当△PMN周长最小时,下列结论:①等于;②等于;③等于;④△PMN周长最小值是5:⑤△PMN周长最小值是10;⑥△PMN周长最小值是15.其中正确结论的序号是 .
三、解答题
18.作图题:(不需证明,只保留作图痕迹)、是两个村庄,、 是一条河流的两岸.
(1)在河岸建立水站,使,试确定点的位置.
(2)在河岸上建立水站,若使管道最短,确定点的位置.
19.如图,在锐角中,,,平分,分别是和上的动点,求的最小值并说明理由.
20.如图,在平面直角坐标系中,△ABC三个顶点的坐标为、、.
(1)在图中作出△ABC关于轴的对称图形△;
(2)请直接写出点的坐标___________;
(3)在轴上画出一点使的值最小.
21.如图,已知点A,B,C,D是不在同一直线上的四个点,请按要求画出图形.
(1)作线段和射线;
(2)用无刻度的直尺和圆规在射线上作;
(3)在平面内作一点P,使得的和最短.
参考答案:
1.C
2.C
3.D
4.D
5.D
6.B
7.A
8.B
9.B
10.B
11.C
12.C
13.两点之间线段最短
14.
15.
16.5
17.①⑤/⑤①
18.(1)如图所示,点为所找到的位置.
(2)如图所示,点为所找到的位置.
19.
20.解:(1)根据题意得:点、、关于轴的对称的的对应点分别为、、,画出图形,如图所示:
(2)点的坐标为;
(3)如图,作点关于 轴的对称点 ,连接 交 轴于点 ,则点即为所求,
∵点 与 关于轴对称,
∴ ,
∴,
即当点 三点共线时,的值最小.
21.(1)解:如图:
(2)解:如图:
(3)解:点P即为所求.
两点之间线段最短,
要使得的和最短,则点应为线段和线段的交点.
