第十一章三角形章节训练(含答案)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 第十一章三角形章节训练(含答案)2023-2024学年人教版八年级数学上册 | 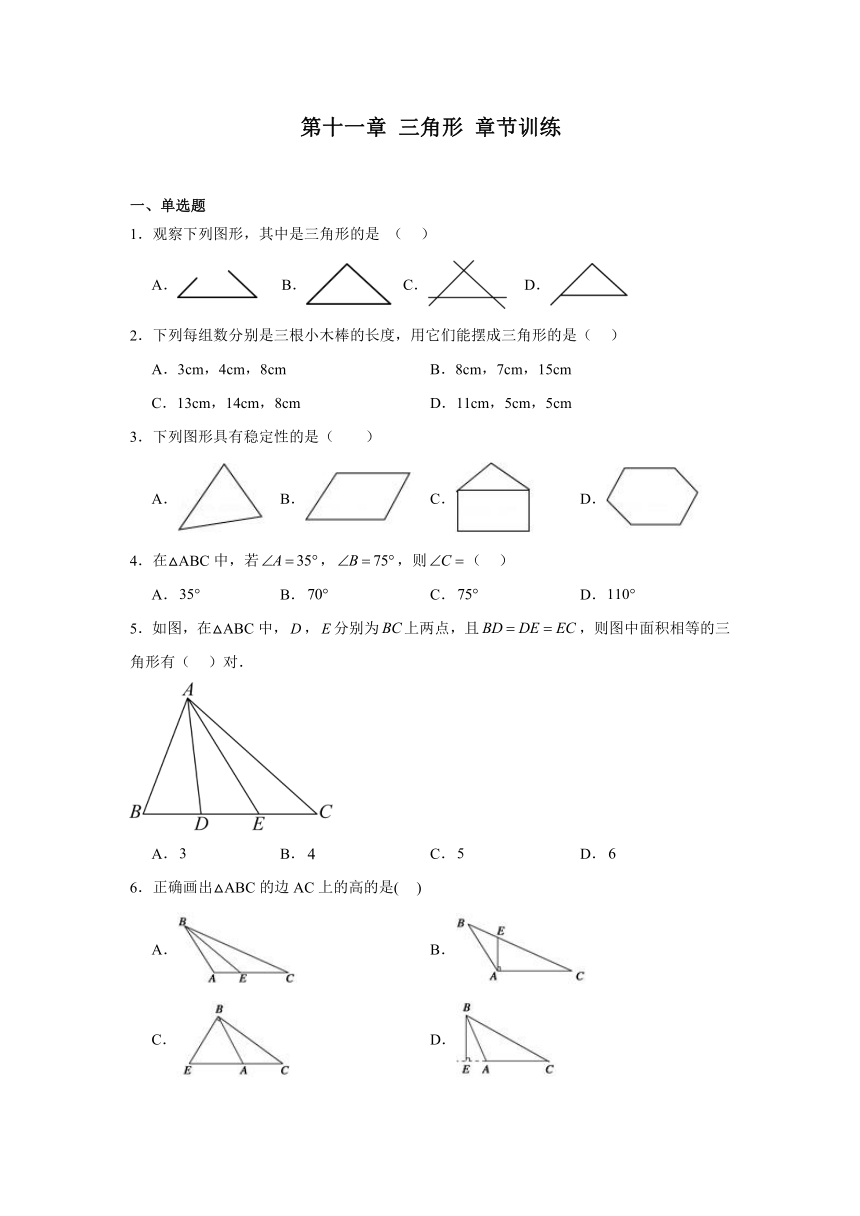 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 16:13:30 | ||
图片预览



文档简介
第十一章 三角形 章节训练
一、单选题
1.观察下列图形,其中是三角形的是 ( )
A. B. C. D.
2.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.13cm,14cm,8cm D.11cm,5cm,5cm
3.下列图形具有稳定性的是( )
A. B. C. D.
4.在△ABC中,若,,则( )
A. B. C. D.
5.如图,在△ABC中,,分别为上两点,且,则图中面积相等的三角形有( )对.
A. B. C. D.
6.正确画出△ABC的边AC上的高的是( )
A. B.
C. D.
7.等腰直角三角形的腰长为,该三角形的重心到斜边的距离为( )
A. B. C. D.
8.将一副三角尺按如图方式进行摆放,则∠1的度数为( )
A. B. C. D.
9.如图,足球图片正中的黑色正五边形的内角和是( )
A. B. C. D.
10.若a,b,c是△ABC的三边长,则化简|a-b-c|+|a+c-b|-|c-a-b|=( )
A.3a-b-c B.-a-b+3c C.a+b+c D.a-3b+c
11.下列说法:①如果,那么△ABC是直角三角形;②各个角都相等的多边形是正多边形;③三角形的外角大于内角,其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
12.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A.360° B.720° C.540° D.240°
13.如图,网格图中每个小正方形的边长均为1,以为半径的扇形经过平移到达扇形的位置,那么图中阴影部分的面积是( ).
A.8 B.6 C.6.5 D.7.5
14.如图,是一个等边三角形木框,甲虫在边框上爬行(,端点除外),设甲虫到另外两边的距离之和为d,等边三角形的高为,则d与的大小关系是( )
A. B. C. D.无法确定
二、填空题
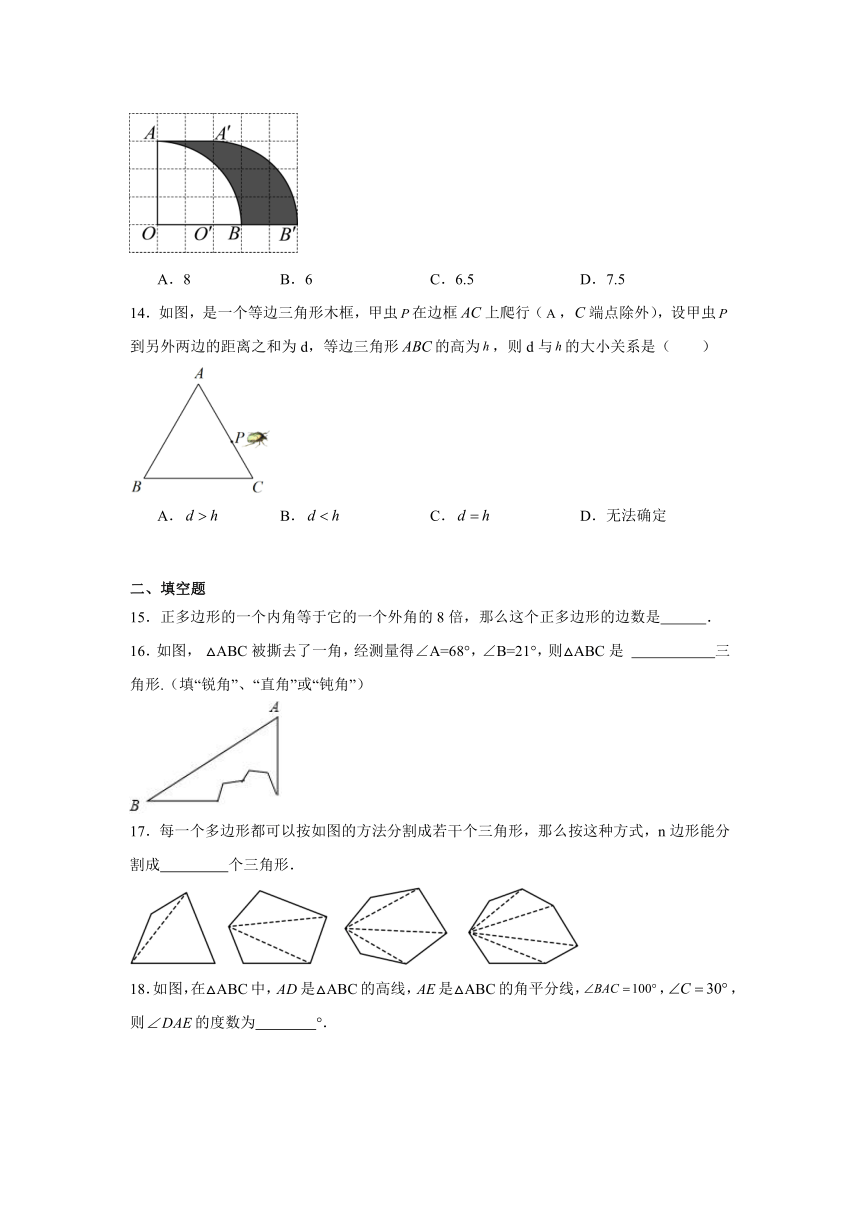
15.正多边形的一个内角等于它的一个外角的8倍,那么这个正多边形的边数是 .
16.如图, △ABC被撕去了一角,经测量得∠A=68°,∠B=21°,则△ABC是 三角形.(填“锐角”、“直角”或“钝角”)
17.每一个多边形都可以按如图的方法分割成若干个三角形,那么按这种方式,n边形能分割成 个三角形.
18.如图,在△ABC中,是△ABC的高线,是△ABC的角平分线,,,则的度数为 °.
19.已知AD是△ABC的中线,若△ABD与△ACD的周长分别是14和12.△ABC的周长是20,则AD的长为 .
20.如图所示,已知,,,则等于 .
21.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S1﹣S2=a,则S△ABC= .
22.如图是国家级非物质文化遗产——“抖空竹”.在“抖空竹”的一个瞬间如图①所示,若将图①抽象成图②的数学问题:,,,则的大小是 度.
23.用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间没有空隙,也没有重叠地铺成一片,叫做图形的密铺.例如,图1和图2是用全等的三角形或四边形材料密铺
而成的地面.若用边长相同的 个正三角形和个正六边形材料组合密铺地面,则和满足关系式是 .
三、解答题
24.如图所示方格纸中,每个小正方形的边长均为l,点,点,点在小正方形的顶点上.
(1)画出△ABC中边上的高;
(2)画出△ABC中边上的中线;
(3)直接写出△ABC的面积为________.
25.如图,为△ABC的高,为的角平分线,若,.求的度数.
26.如图,在△ABC中,是边上的中线,的周长是.求的长.
27.如图,在△ABC中点D是AC上一点,连接BD,点E是BD上一点,连接CE,求证:∠2+∠3=∠1﹣∠A.
28.如图,在直角△ABC中,,是边上的高,是边上的中线,,,,求:
(1)的长;
(2) △BCE的面积.
参考答案:
1.B
2.C
3.A
4.B
5.B
6.D
7.D
8.C
9.B
10.B
11.B
12.D
13.B
14.C
15.18
16.钝角
17.
18.
19.3
20.
21.6a
22.40
23.
24.(1)解:如图,
线段即为所求;
(2)如图,
线段即为所求;
(3)8
25..
26.
27.∵∠1=∠3+∠BDC,∠BDC=∠2+∠A,
∴∠1=∠3+∠2+∠A,
∴∠1-∠A=∠2+∠3.
28.(1);
(2).
一、单选题
1.观察下列图形,其中是三角形的是 ( )
A. B. C. D.
2.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.13cm,14cm,8cm D.11cm,5cm,5cm
3.下列图形具有稳定性的是( )
A. B. C. D.
4.在△ABC中,若,,则( )
A. B. C. D.
5.如图,在△ABC中,,分别为上两点,且,则图中面积相等的三角形有( )对.
A. B. C. D.
6.正确画出△ABC的边AC上的高的是( )
A. B.
C. D.
7.等腰直角三角形的腰长为,该三角形的重心到斜边的距离为( )
A. B. C. D.
8.将一副三角尺按如图方式进行摆放,则∠1的度数为( )
A. B. C. D.
9.如图,足球图片正中的黑色正五边形的内角和是( )
A. B. C. D.
10.若a,b,c是△ABC的三边长,则化简|a-b-c|+|a+c-b|-|c-a-b|=( )
A.3a-b-c B.-a-b+3c C.a+b+c D.a-3b+c
11.下列说法:①如果,那么△ABC是直角三角形;②各个角都相等的多边形是正多边形;③三角形的外角大于内角,其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
12.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A.360° B.720° C.540° D.240°
13.如图,网格图中每个小正方形的边长均为1,以为半径的扇形经过平移到达扇形的位置,那么图中阴影部分的面积是( ).
A.8 B.6 C.6.5 D.7.5
14.如图,是一个等边三角形木框,甲虫在边框上爬行(,端点除外),设甲虫到另外两边的距离之和为d,等边三角形的高为,则d与的大小关系是( )
A. B. C. D.无法确定
二、填空题
15.正多边形的一个内角等于它的一个外角的8倍,那么这个正多边形的边数是 .
16.如图, △ABC被撕去了一角,经测量得∠A=68°,∠B=21°,则△ABC是 三角形.(填“锐角”、“直角”或“钝角”)
17.每一个多边形都可以按如图的方法分割成若干个三角形,那么按这种方式,n边形能分割成 个三角形.
18.如图,在△ABC中,是△ABC的高线,是△ABC的角平分线,,,则的度数为 °.
19.已知AD是△ABC的中线,若△ABD与△ACD的周长分别是14和12.△ABC的周长是20,则AD的长为 .
20.如图所示,已知,,,则等于 .
21.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S1﹣S2=a,则S△ABC= .
22.如图是国家级非物质文化遗产——“抖空竹”.在“抖空竹”的一个瞬间如图①所示,若将图①抽象成图②的数学问题:,,,则的大小是 度.
23.用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间没有空隙,也没有重叠地铺成一片,叫做图形的密铺.例如,图1和图2是用全等的三角形或四边形材料密铺
而成的地面.若用边长相同的 个正三角形和个正六边形材料组合密铺地面,则和满足关系式是 .
三、解答题
24.如图所示方格纸中,每个小正方形的边长均为l,点,点,点在小正方形的顶点上.
(1)画出△ABC中边上的高;
(2)画出△ABC中边上的中线;
(3)直接写出△ABC的面积为________.
25.如图,为△ABC的高,为的角平分线,若,.求的度数.
26.如图,在△ABC中,是边上的中线,的周长是.求的长.
27.如图,在△ABC中点D是AC上一点,连接BD,点E是BD上一点,连接CE,求证:∠2+∠3=∠1﹣∠A.
28.如图,在直角△ABC中,,是边上的高,是边上的中线,,,,求:
(1)的长;
(2) △BCE的面积.
参考答案:
1.B
2.C
3.A
4.B
5.B
6.D
7.D
8.C
9.B
10.B
11.B
12.D
13.B
14.C
15.18
16.钝角
17.
18.
19.3
20.
21.6a
22.40
23.
24.(1)解:如图,
线段即为所求;
(2)如图,
线段即为所求;
(3)8
25..
26.
27.∵∠1=∠3+∠BDC,∠BDC=∠2+∠A,
∴∠1=∠3+∠2+∠A,
∴∠1-∠A=∠2+∠3.
28.(1);
(2).
