江西省2007年高考试卷分析与评价(江西省南昌市)
文档属性
| 名称 | 江西省2007年高考试卷分析与评价(江西省南昌市) |  | |
| 格式 | rar | ||
| 文件大小 | 380.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-12 21:52:00 | ||
图片预览









文档简介
课件35张PPT。 2007年江西高考数学试题评析 赣州市教研室 袁明生
2007年10月
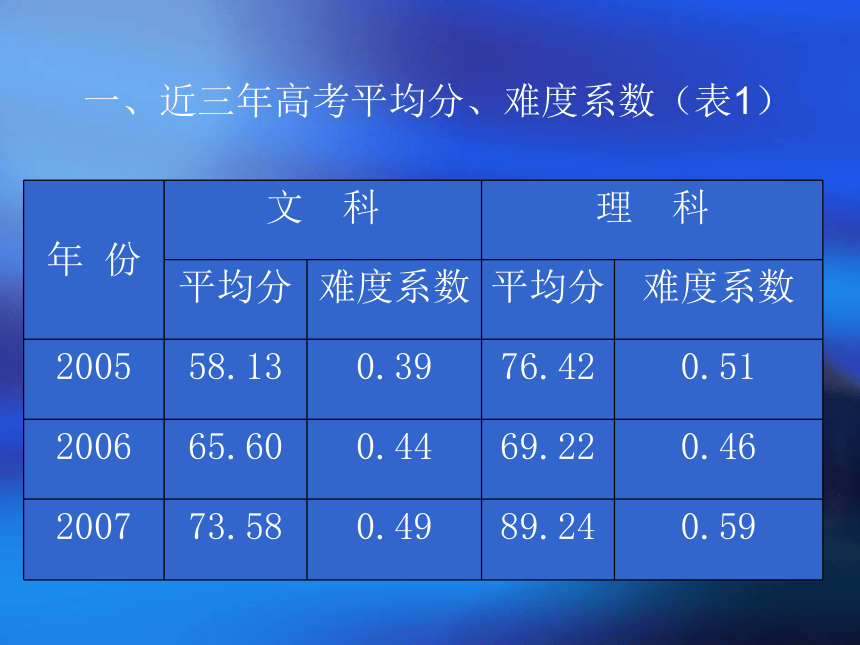
ndyms@126.com 13033220163一、总体评价 2007年江西高考数学试题以《考试大纲》为依据,科学地考查了学生继续学习所应具备的数学素养和潜能,注重对数学本质理解的考查,为高校录取新生提供了有效的数学成绩.试题贴近中学教学,结合中学数学的知识、思想方法和能力等要求,贯彻新课程的理念,符合现行中学课程的实际,试题立意朴实但又不失新颖,选材寓于教材又高于教材,发挥了良好的导向作用.一、近三年高考平均分、难度系数(表1)
由表1可以看出以下几个问题:
1、06年的理科试题偏难,07年得
理科试题偏易.
2、05年的文科试题较难,07年文
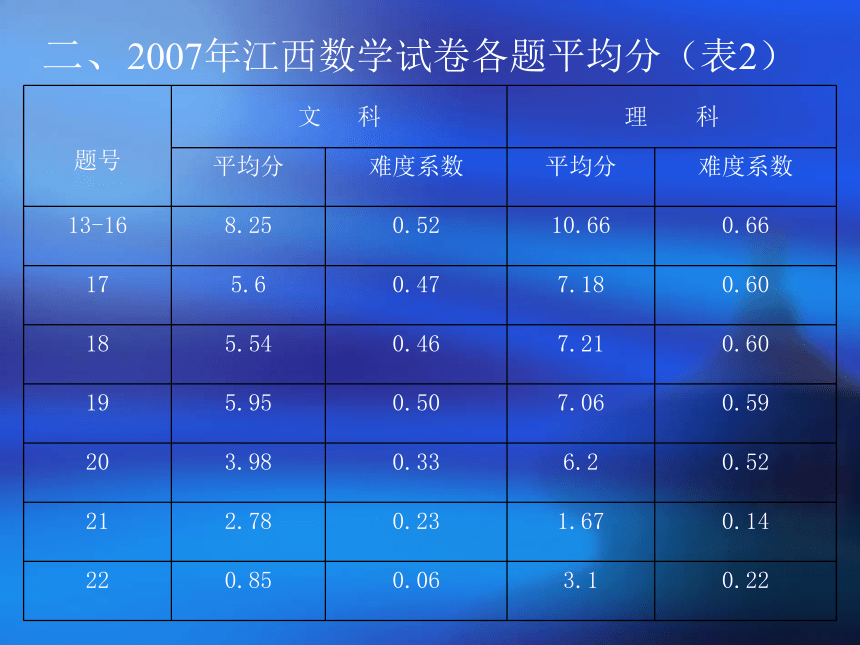
科试题较易. 二、2007年江西数学试卷各题平均分(表2)
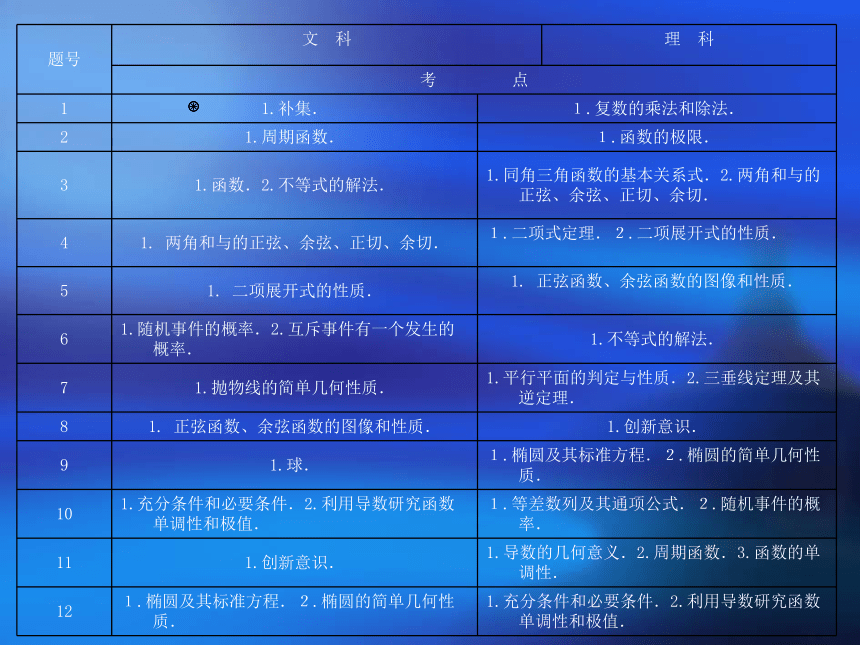
三、试卷考点分布(表3) 按《考试大纲》
(1)理科(A)有132个知识点,理科(B)有
138个知识点;
(2)文科(A)有116知识点,文科(B)有
122个知识点.
(3)由上表可知:文科试卷考查了33个知识
点;理科试卷考查了42个知识点.四、试卷基本特点1.由于前两年数学试题偏难,07年试题根据考生的实际情况,命题组降低了试卷的难度,具体可以从以下几个方面看出:
(1)试题控制试卷入口题的难度.文、理科选择题的前4题,填空题第一题,解答题第一题,难度较低,基本属于课本中的练习题或习题,它对中学数学教学的有很好的导向作用.(2)控制新题型的比例.无论是设问方式新颖的试题、情境设置新颖的试题,还是应用型试题,对考生来说都比常规题难,这类题的多少与难易会直接影响整份试卷的难度.07年试卷中文、理科各只有一题.这对保持试卷的总体难度的稳定起到了保障作用.
(3)控制较难题的比例.为了充分体现试卷的选拔功能,设置适量的较难题是必要的,关键是如何把握其数量和难度,今年的试卷比较适度,难题文科有最后三题,理科有最后两题.而选择题、填空题基本上没有难题.(4)较难的解答题采用分步设问,分步给分的设计方法。试卷中后面的几个解答题往往较难,为了降低难度,试卷采用分步设问的办法使其逐步深入,这样即可化解试题难度,又能合理区分不同层次的考生.2.试卷突出理性思维,倡导通性通法 数学思想方法是对数学知识的最高层次的概括与提炼,是适用于中学数学全部内容的通法,是高考的核心.转化与化归的思想、函数与方程的思想、数形结合的思想、分类与整合的思想,解析法、数学归纳法、换元法、割补法、配方法等等是考查的重点;如:理科的第5题、第6题、第10题、第17题、第20题、第21题、第22题.文科第8题、第17题、第20题等. 3.正确区分文理科考生 命题注意到文、理科考生在数学学习上的差异以及高校对文、理科考生的不同要求,对文、理科考生坚持不同的考查标准。试卷文理科完全相同题3道,共24分,姊妹题6道,共52分.总分76(2005年90分).这样设计试题,有利于降低文科试题难度,激发文科学生学习数学的兴趣.
五、试题分析1. (理5)若 ,则下列命题中正确的是( )
A. B.
C. D.
(评析)利用 的图像易
得答案D;特殊值法:取 ,可排除
A、B、C.2.(理8、文11)四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示,盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为 , , , ,则它们的大小关系正确的是( )
A. B. C. D.
(评析)展露新意、闪现亮点是高考命题者所追求的,本题知识虽然是新的,能力却没有超纲,以考生熟悉的生活用品考查空间想象能力、逻辑推理能力。3.(理14)已知数列 对于任意 ,有 ,若 ,则 .
解:令 ,得 ,所以 是公差为 、首项也为 的等差数列, .
另解:
(评析)在中 ,取 ,得
等等.这种取特殊值的方法,显示出由一般到特殊的思维方式,事实上,本题的数列当中隐含了一个子数列是等比数列.4.如图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为 .已知 ,
, .
(1)设点 是 的中点,证明: ∥平面 ;
(2)求二面角 的大小;
(3)求此几何体的体积.解:取 的中点 , 的中点 ,连接 、 ,易证 ,
,则平面 ,故 .
(2)过点 作 ,垂足为 ,再过点
作 ,垂足为 ,连接 .由 ,可得 为二面角的平面角.
(评析)本题以“残缺”的几何体为背景来设计问题.但考查的重点内容依然不变.本题学生的主要困难在于找二面角的平面角以及用割补法求几何体体积.从第二问来说传统方法要比向量方法更难一些. 5.设动点 到 点 和的距离分别为 和 , ,且存在常数
,使得 .
(1)证明:动点 的轨迹 为双曲线,并求出 的方程;
(2)过点 作直线 交双曲线的右支于 、 两点,试确定 的范围,使
其中点 为坐标原点. 另解:(2)设 直线的方程为 ,代入 ,得 .
.
从而
所以 ,
又 .则 , ,
又 点在双曲线的右支上,故 ,
(评析)假设 所在直线方程为 ,一是避免了对直线的斜率是否存在的讨论;二是直接由
建立了关于 的不等式,
回避了对曲线范围的讨论.运用韦达定理的解题方法是解析几何中解决直线与圆锥曲线问题的核心方法.这一题平均得分不到2分,是得分最低的一题,说明大部分学生都没有完成第一问.主要问题出在学生把已知条件 与三角形面积联系起来,以至做不下去.6.(理22)设正整数数列 满足: ,且对
于任何 ,有 .
(1)求 , ;
(3)求数列 的通项 .
(评析)本题以繁分式不等式给出的递推关系,形式比较少见,学生望而生畏.第二问的证明有两个难关:(1).繁分式的变形;(2).“不等”与“等”之间的转化.六、2008年复习建议1.高考数学复习的目的和任务是什么?
(1)查缺补漏,梳理知识,形成完整的知识网络,整体把握数学认知结构;
(2)进一步巩固和掌握三基;
(3)总结规律,加深理解,促进理性思维能力的发展;
(4)强化思维训练,提高解题能力和探索创新能力,发展数学智慧.2.夯实三基 避免遗漏
基本知识、基本技能和基本数学思想方法一直是高考的重点,“三基”是一切的源头,而运算能力是重中之重,数学思想方法对简化运算、优化解题过程和提高解题速度起到把握方向和调控作用.对书上内容、局部知识要按照一定方法和观点进行整理,基本技能和思想方法渗透其中,这样才能形成认知体系.要注意全面复习知识,不能有欠缺,如正态分布.
(2007安徽理10).以 表示标准正态总体在区间 内取值的概率,若随机变量
服从正态分布 ,则概率 等于( )
A. B.
C. D.
(2006湖北理20).在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 .已知成绩在90分以上(含90分)的学生有12名.
(1).试问此次参赛学生总数约为多少人?
(2).若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?(2007浙江5)已知随机变量 服从正态分布 , , 则 ( )
A. 0.16 B. 0.32 C.0.68 D.0.84
(2007全国2 14).在某项测量中,测量结果
服从正态分布 .若 在 内取值的概率为0.4,则 在 内取值的概率为 .
(2007湖南理5).设随机变量 服从标准正态分布 ,已知 ,则
=( )
A.0.025 B.0.050
C.0.950 D.0.975(2007广东理)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗 (吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关
于 的线性回归方程 ;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨
标准煤.试根据(2)求出的线性回归方程,预
测生产100吨甲产品的生产能耗比技改前降低多
少吨标准煤?(参考数值: )3.构建网络,突出主干
数学教学的本质是在数学知识的教学中在学生主动参与、积极建构的基础之上,把大量的数学概念、定理、公式等知识,进行加工,形成越来越有层次的数学知识网络结构,居高临下地解决问题,因此,在平时教学及高三复习中要把整个高中知识按章节间的逻辑联系,帮助学生拿到问题便知道用什么知识,什么方法解决.
高中主干知识有:函数、数列、三角函数、立体几何、概率、导数及解析几何等,高考试题以主干知识为主,常考常新,复习中应以主干知识为主进行,特别注重它们之间的交叉融合.六、试题中值得商榷的问题1、图形不规范.
(理)第7题 (理)第15题 (文)第20题
(文)第16题 (理)第20题2.理科试卷中中档题并没有起到中档题的作
用,使得整卷区分度不是太好.
3.压轴题最好不要年年都用递推数列.这样容易
使考生猜题压宝.
(2006年理)22.已知数列 满足: ,且
(1)求数列 的通项公式;
(2)证明:对于一切正整数n,不等式
. (2006年文)22.已知各项均为正数的数列 满足: ,
且 .
(1)求数列 的通项公式;
(2)设 ,求 .并确定最小正整数 .使 为整数.
(2005年文)22. 已知数列 的前项 和满足 ,求数列 的通项公式.
(2005年理)21. 已知数列 的各项都是正数,且满足 .
(1)证明 ;
(2)求数列 的通项公式 .
谢谢!
2007年10月
ndyms@126.com 13033220163一、总体评价 2007年江西高考数学试题以《考试大纲》为依据,科学地考查了学生继续学习所应具备的数学素养和潜能,注重对数学本质理解的考查,为高校录取新生提供了有效的数学成绩.试题贴近中学教学,结合中学数学的知识、思想方法和能力等要求,贯彻新课程的理念,符合现行中学课程的实际,试题立意朴实但又不失新颖,选材寓于教材又高于教材,发挥了良好的导向作用.一、近三年高考平均分、难度系数(表1)
由表1可以看出以下几个问题:
1、06年的理科试题偏难,07年得
理科试题偏易.
2、05年的文科试题较难,07年文
科试题较易. 二、2007年江西数学试卷各题平均分(表2)
三、试卷考点分布(表3) 按《考试大纲》
(1)理科(A)有132个知识点,理科(B)有
138个知识点;
(2)文科(A)有116知识点,文科(B)有
122个知识点.
(3)由上表可知:文科试卷考查了33个知识
点;理科试卷考查了42个知识点.四、试卷基本特点1.由于前两年数学试题偏难,07年试题根据考生的实际情况,命题组降低了试卷的难度,具体可以从以下几个方面看出:
(1)试题控制试卷入口题的难度.文、理科选择题的前4题,填空题第一题,解答题第一题,难度较低,基本属于课本中的练习题或习题,它对中学数学教学的有很好的导向作用.(2)控制新题型的比例.无论是设问方式新颖的试题、情境设置新颖的试题,还是应用型试题,对考生来说都比常规题难,这类题的多少与难易会直接影响整份试卷的难度.07年试卷中文、理科各只有一题.这对保持试卷的总体难度的稳定起到了保障作用.
(3)控制较难题的比例.为了充分体现试卷的选拔功能,设置适量的较难题是必要的,关键是如何把握其数量和难度,今年的试卷比较适度,难题文科有最后三题,理科有最后两题.而选择题、填空题基本上没有难题.(4)较难的解答题采用分步设问,分步给分的设计方法。试卷中后面的几个解答题往往较难,为了降低难度,试卷采用分步设问的办法使其逐步深入,这样即可化解试题难度,又能合理区分不同层次的考生.2.试卷突出理性思维,倡导通性通法 数学思想方法是对数学知识的最高层次的概括与提炼,是适用于中学数学全部内容的通法,是高考的核心.转化与化归的思想、函数与方程的思想、数形结合的思想、分类与整合的思想,解析法、数学归纳法、换元法、割补法、配方法等等是考查的重点;如:理科的第5题、第6题、第10题、第17题、第20题、第21题、第22题.文科第8题、第17题、第20题等. 3.正确区分文理科考生 命题注意到文、理科考生在数学学习上的差异以及高校对文、理科考生的不同要求,对文、理科考生坚持不同的考查标准。试卷文理科完全相同题3道,共24分,姊妹题6道,共52分.总分76(2005年90分).这样设计试题,有利于降低文科试题难度,激发文科学生学习数学的兴趣.
五、试题分析1. (理5)若 ,则下列命题中正确的是( )
A. B.
C. D.
(评析)利用 的图像易
得答案D;特殊值法:取 ,可排除
A、B、C.2.(理8、文11)四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示,盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为 , , , ,则它们的大小关系正确的是( )
A. B. C. D.
(评析)展露新意、闪现亮点是高考命题者所追求的,本题知识虽然是新的,能力却没有超纲,以考生熟悉的生活用品考查空间想象能力、逻辑推理能力。3.(理14)已知数列 对于任意 ,有 ,若 ,则 .
解:令 ,得 ,所以 是公差为 、首项也为 的等差数列, .
另解:
(评析)在中 ,取 ,得
等等.这种取特殊值的方法,显示出由一般到特殊的思维方式,事实上,本题的数列当中隐含了一个子数列是等比数列.4.如图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为 .已知 ,
, .
(1)设点 是 的中点,证明: ∥平面 ;
(2)求二面角 的大小;
(3)求此几何体的体积.解:取 的中点 , 的中点 ,连接 、 ,易证 ,
,则平面 ,故 .
(2)过点 作 ,垂足为 ,再过点
作 ,垂足为 ,连接 .由 ,可得 为二面角的平面角.
(评析)本题以“残缺”的几何体为背景来设计问题.但考查的重点内容依然不变.本题学生的主要困难在于找二面角的平面角以及用割补法求几何体体积.从第二问来说传统方法要比向量方法更难一些. 5.设动点 到 点 和的距离分别为 和 , ,且存在常数
,使得 .
(1)证明:动点 的轨迹 为双曲线,并求出 的方程;
(2)过点 作直线 交双曲线的右支于 、 两点,试确定 的范围,使
其中点 为坐标原点. 另解:(2)设 直线的方程为 ,代入 ,得 .
.
从而
所以 ,
又 .则 , ,
又 点在双曲线的右支上,故 ,
(评析)假设 所在直线方程为 ,一是避免了对直线的斜率是否存在的讨论;二是直接由
建立了关于 的不等式,
回避了对曲线范围的讨论.运用韦达定理的解题方法是解析几何中解决直线与圆锥曲线问题的核心方法.这一题平均得分不到2分,是得分最低的一题,说明大部分学生都没有完成第一问.主要问题出在学生把已知条件 与三角形面积联系起来,以至做不下去.6.(理22)设正整数数列 满足: ,且对
于任何 ,有 .
(1)求 , ;
(3)求数列 的通项 .
(评析)本题以繁分式不等式给出的递推关系,形式比较少见,学生望而生畏.第二问的证明有两个难关:(1).繁分式的变形;(2).“不等”与“等”之间的转化.六、2008年复习建议1.高考数学复习的目的和任务是什么?
(1)查缺补漏,梳理知识,形成完整的知识网络,整体把握数学认知结构;
(2)进一步巩固和掌握三基;
(3)总结规律,加深理解,促进理性思维能力的发展;
(4)强化思维训练,提高解题能力和探索创新能力,发展数学智慧.2.夯实三基 避免遗漏
基本知识、基本技能和基本数学思想方法一直是高考的重点,“三基”是一切的源头,而运算能力是重中之重,数学思想方法对简化运算、优化解题过程和提高解题速度起到把握方向和调控作用.对书上内容、局部知识要按照一定方法和观点进行整理,基本技能和思想方法渗透其中,这样才能形成认知体系.要注意全面复习知识,不能有欠缺,如正态分布.
(2007安徽理10).以 表示标准正态总体在区间 内取值的概率,若随机变量
服从正态分布 ,则概率 等于( )
A. B.
C. D.
(2006湖北理20).在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 .已知成绩在90分以上(含90分)的学生有12名.
(1).试问此次参赛学生总数约为多少人?
(2).若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?(2007浙江5)已知随机变量 服从正态分布 , , 则 ( )
A. 0.16 B. 0.32 C.0.68 D.0.84
(2007全国2 14).在某项测量中,测量结果
服从正态分布 .若 在 内取值的概率为0.4,则 在 内取值的概率为 .
(2007湖南理5).设随机变量 服从标准正态分布 ,已知 ,则
=( )
A.0.025 B.0.050
C.0.950 D.0.975(2007广东理)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗 (吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关
于 的线性回归方程 ;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨
标准煤.试根据(2)求出的线性回归方程,预
测生产100吨甲产品的生产能耗比技改前降低多
少吨标准煤?(参考数值: )3.构建网络,突出主干
数学教学的本质是在数学知识的教学中在学生主动参与、积极建构的基础之上,把大量的数学概念、定理、公式等知识,进行加工,形成越来越有层次的数学知识网络结构,居高临下地解决问题,因此,在平时教学及高三复习中要把整个高中知识按章节间的逻辑联系,帮助学生拿到问题便知道用什么知识,什么方法解决.
高中主干知识有:函数、数列、三角函数、立体几何、概率、导数及解析几何等,高考试题以主干知识为主,常考常新,复习中应以主干知识为主进行,特别注重它们之间的交叉融合.六、试题中值得商榷的问题1、图形不规范.
(理)第7题 (理)第15题 (文)第20题
(文)第16题 (理)第20题2.理科试卷中中档题并没有起到中档题的作
用,使得整卷区分度不是太好.
3.压轴题最好不要年年都用递推数列.这样容易
使考生猜题压宝.
(2006年理)22.已知数列 满足: ,且
(1)求数列 的通项公式;
(2)证明:对于一切正整数n,不等式
. (2006年文)22.已知各项均为正数的数列 满足: ,
且 .
(1)求数列 的通项公式;
(2)设 ,求 .并确定最小正整数 .使 为整数.
(2005年文)22. 已知数列 的前项 和满足 ,求数列 的通项公式.
(2005年理)21. 已知数列 的各项都是正数,且满足 .
(1)证明 ;
(2)求数列 的通项公式 .
谢谢!
同课章节目录
