第十一章 三角形 单元练习(含答案) 2023——2024学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 单元练习(含答案) 2023——2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 73.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 00:00:00 | ||
图片预览

文档简介
第十一章 三角形
一、选择题
1.下列长度的三条线段,能构成三角形的是( )
A.3 ,10 ,5 B.4 ,8 ,4
C.5 ,13 ,12 D.2 ,7 ,4
2.在△ABC中,∠A=60°,∠B=50°,则∠C的度数为( )
A.60° B.30° C.70° D.50°
3.要使如图的六边形框架形状稳定,至少需要添加对角线的条数是( )
A. B. C. D.
4.如果一个多边形的每一个外角都是45°,那么这个多边形的内角和是( )
A.540° B.720° C.1080° D.1260°
5.如图,在中,,,那么的度数为( )
A. B. C. D.
6.如图,在 中,A B=2020,AC=2018,AD为中线,则 与 的周长之差为( )
A.1 B.2 C.3 D.4
7.如图,根据图上标注的信息,则 的大小( )
A.100° B.105° C.115° D.120°
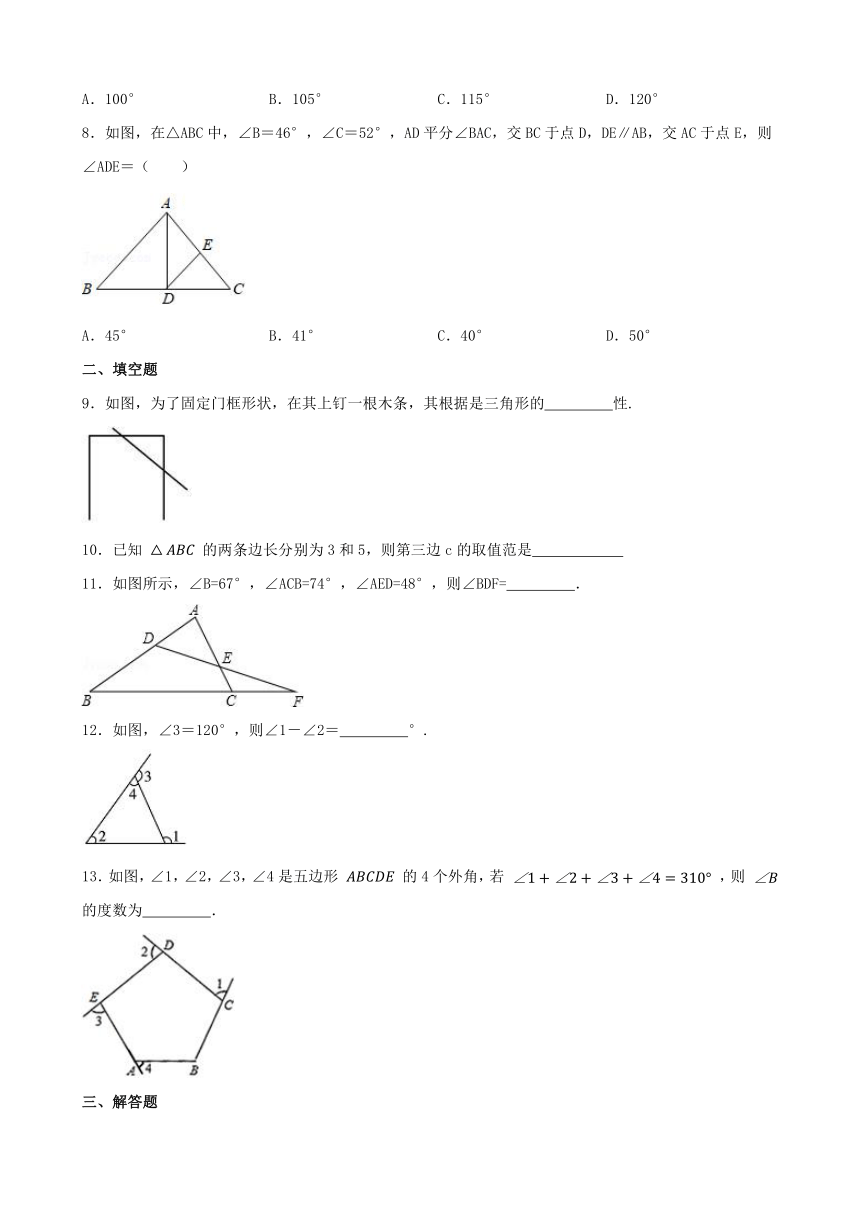
8.如图,在△ABC中,∠B=46°,∠C=52°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE=( )
A.45° B.41° C.40° D.50°
二、填空题
9.如图,为了固定门框形状,在其上钉一根木条,其根据是三角形的 性.
10.已知 的两条边长分别为3和5,则第三边c的取值范是
11.如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF= .
12.如图,∠3=120°,则∠1-∠2= °.
13.如图,∠1,∠2,∠3,∠4是五边形 的4个外角,若 ,则 的度数为 .
三、解答题
14.已知三角形的两边 ,若第三边 的长为偶数,求其周长.
15.如图,在△ABC中,∠ABC、∠ACB的平分线BE,CD相交于点F,已知∠ABC=40°,∠A=60°,求∠BFD的度数.
16.如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
17.如图,已知点 是四边形 的外角 和外角 的平分线的交点.若 , ,求 的度数.
18.如图,在四边形中,平分交于点,连接.
(1)若,,,求的度数.
(2)若,,求证:.
参考答案
1.C
2.C
3.C
4.C
5.C
6.B
7.D
8.B
9.稳定
10.2<c<8
11.87°
12.60
13.130°
14.解:∵三角形的两边的长分别为3和7,
∴第三边c的取值范围为:4<c<10,
∴符合条件的偶数为6或8,
∴当c=6时,这个三角形周长为:3+6+7=16;
当c=8时,这个三角形周长为:3+8+7=18.
∴这个三角形周长为16或18.
15.解:∵∠A=60°
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)=60°,
∵∠BFD=∠FBC+∠FCB,
∴∠BFD=60°.
16.解:在△ABC中,
∵∠BAC:∠B:∠C=4:3:2,
∴∠BAC=180°× =80°,∠B=180°× =60°,
∵AD是BC边上的高线,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=30°,
∵AE平分∠BAC,
∴∠BAE= ∠BAC=40°,
∴∠DAE=∠BAE﹣∠BAD=10°.
17.解:因为 , , ,
所以 .
因为 , ,
所以 .
因为点 是四边形 的外角 和外角 的平分线的交点,
所以 , .
所以 ,
所以 .
18.(1)解:在中,,,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵,
∴.
∵,,
∴.
∵平分,
∴,
∴.
一、选择题
1.下列长度的三条线段,能构成三角形的是( )
A.3 ,10 ,5 B.4 ,8 ,4
C.5 ,13 ,12 D.2 ,7 ,4
2.在△ABC中,∠A=60°,∠B=50°,则∠C的度数为( )
A.60° B.30° C.70° D.50°
3.要使如图的六边形框架形状稳定,至少需要添加对角线的条数是( )
A. B. C. D.
4.如果一个多边形的每一个外角都是45°,那么这个多边形的内角和是( )
A.540° B.720° C.1080° D.1260°
5.如图,在中,,,那么的度数为( )
A. B. C. D.
6.如图,在 中,A B=2020,AC=2018,AD为中线,则 与 的周长之差为( )
A.1 B.2 C.3 D.4
7.如图,根据图上标注的信息,则 的大小( )
A.100° B.105° C.115° D.120°
8.如图,在△ABC中,∠B=46°,∠C=52°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE=( )
A.45° B.41° C.40° D.50°
二、填空题
9.如图,为了固定门框形状,在其上钉一根木条,其根据是三角形的 性.
10.已知 的两条边长分别为3和5,则第三边c的取值范是
11.如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF= .
12.如图,∠3=120°,则∠1-∠2= °.
13.如图,∠1,∠2,∠3,∠4是五边形 的4个外角,若 ,则 的度数为 .
三、解答题
14.已知三角形的两边 ,若第三边 的长为偶数,求其周长.
15.如图,在△ABC中,∠ABC、∠ACB的平分线BE,CD相交于点F,已知∠ABC=40°,∠A=60°,求∠BFD的度数.
16.如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
17.如图,已知点 是四边形 的外角 和外角 的平分线的交点.若 , ,求 的度数.
18.如图,在四边形中,平分交于点,连接.
(1)若,,,求的度数.
(2)若,,求证:.
参考答案
1.C
2.C
3.C
4.C
5.C
6.B
7.D
8.B
9.稳定
10.2<c<8
11.87°
12.60
13.130°
14.解:∵三角形的两边的长分别为3和7,
∴第三边c的取值范围为:4<c<10,
∴符合条件的偶数为6或8,
∴当c=6时,这个三角形周长为:3+6+7=16;
当c=8时,这个三角形周长为:3+8+7=18.
∴这个三角形周长为16或18.
15.解:∵∠A=60°
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)=60°,
∵∠BFD=∠FBC+∠FCB,
∴∠BFD=60°.
16.解:在△ABC中,
∵∠BAC:∠B:∠C=4:3:2,
∴∠BAC=180°× =80°,∠B=180°× =60°,
∵AD是BC边上的高线,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=30°,
∵AE平分∠BAC,
∴∠BAE= ∠BAC=40°,
∴∠DAE=∠BAE﹣∠BAD=10°.
17.解:因为 , , ,
所以 .
因为 , ,
所以 .
因为点 是四边形 的外角 和外角 的平分线的交点,
所以 , .
所以 ,
所以 .
18.(1)解:在中,,,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵,
∴.
∵,,
∴.
∵平分,
∴,
∴.
