第十二章全等三角形章节训练(含答案) 人教版八年级数学上册
文档属性
| 名称 | 第十二章全等三角形章节训练(含答案) 人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 973.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 17:23:02 | ||
图片预览


文档简介
第十二章全等三角形 章节训练
一、单选题
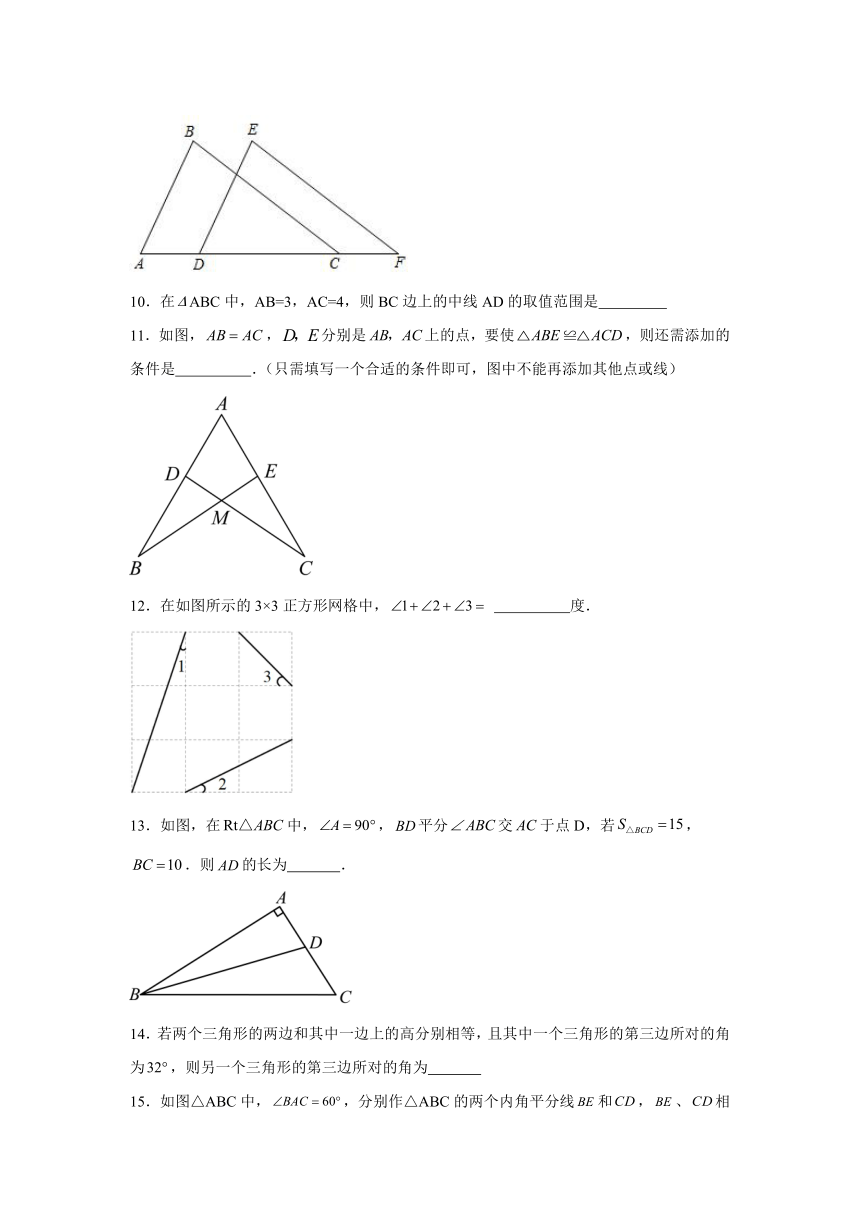
1.下列图形中,与已知图形全等的是( )
A. B. C. D.
2.下列说法不正确的是( )
A.三边分别相等的两个三角形全等
B.有两边及一角对应相等的两个三角形全等
C.有两角及一边对应相等的两个三角形全等
D.斜边和一条直角边分别相等的两个直角三角形全等
3.在△ABC中,∠C=90°,D为AB的中点,ED⊥AB,∠DAE=∠CAE,则 ∠CAB=( )
A.30° B.60° C.80 ° D.50°
4.如图,△ABC中,N是BC边上的中点,AM平分∠BAC,BM⊥AM于点M,若AB=8,MN=2.则AC的长为( )
A.10 B.11 C.12 D.13
5.如图,已知,在下列条件:①;②;③;④中,只补充一个就一定可以判断的条件是( )
A.①②③④ B.①②③ C.②③④ D.①②④
6.如图,已知△ABC的周长是42,分别平分和,于D,且,则△ABC的面积为( )
A.126 B.63 C.42 D.21
7.如图,某三角形材料断裂成Ⅰ、Ⅱ、Ⅲ三块,现要配置与原材料全等的三角形材料,应该利用材料Ⅲ,这样做利用的是三角形全等判定方法中的( )
A.边角边 B.角角边 C.角边角 D.边边边
8.如图,三条笔直公路两两相交,交点分别为,,,现计划修一个油库,要求到三条公路的距离都相等,△ABC内部被河水填满无法施工,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
二、填空题
9.如图,,若,则的度数为 .
10.在ABC中,AB=3,AC=4,则BC边上的中线AD的取值范围是
11.如图,,分别是上的点,要使,则还需添加的条件是 .(只需填写一个合适的条件即可,图中不能再添加其他点或线)
12.在如图所示的3×3正方形网格中, 度.
13.如图,在中,,平分交于点D,若,.则的长为 .
14.若两个三角形的两边和其中一边上的高分别相等,且其中一个三角形的第三边所对的角为,则另一个三角形的第三边所对的角为
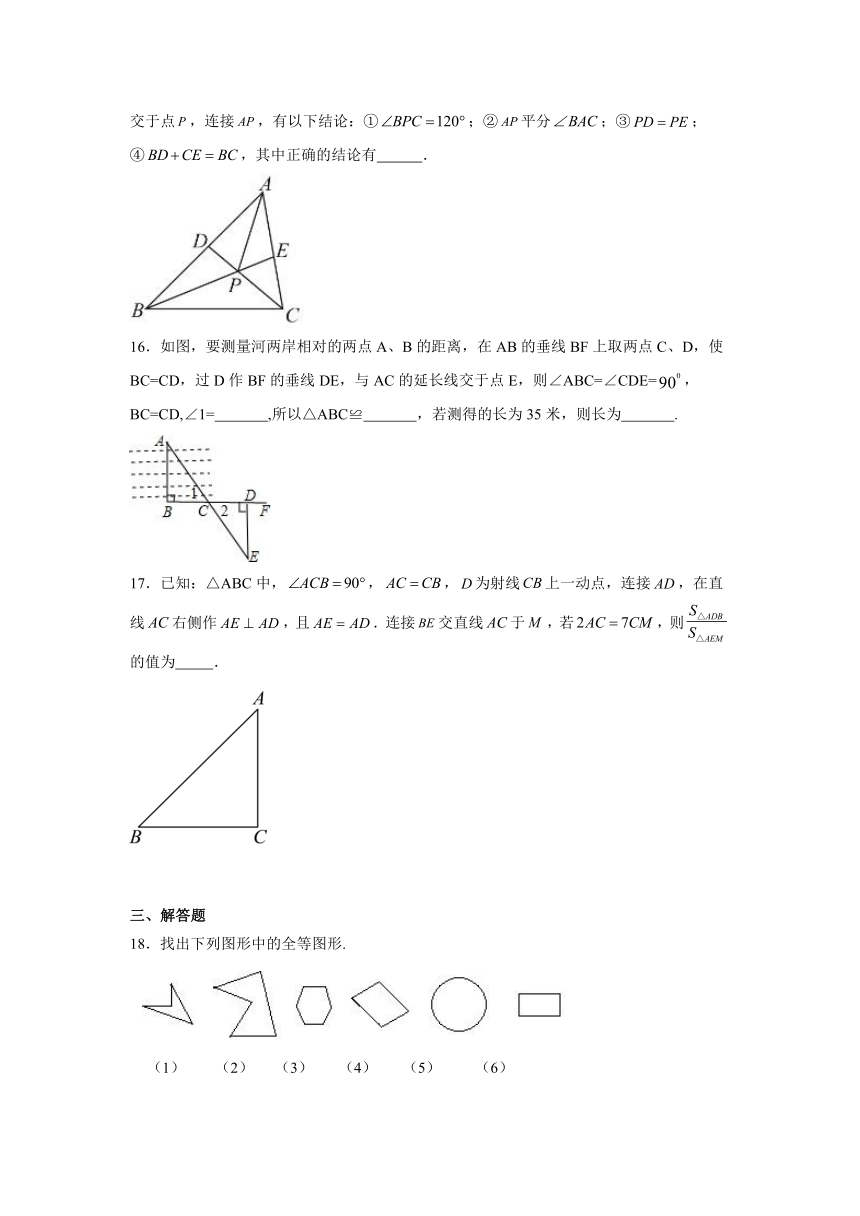
15.如图△ABC中,,分别作△ABC的两个内角平分线和,、相交于点,连接,有以下结论:①;②平分;③;④,其中正确的结论有 .
16.如图,要测量河两岸相对的两点A、B的距离,在AB的垂线BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,则∠ABC=∠CDE=,BC=CD,∠1= ,所以△ABC≌ ,若测得的长为35米,则长为 .
17.已知:△ABC中,,,为射线上一动点,连接,在直线右侧作,且.连接交直线于,若,则的值为 .
三、解答题
18.找出下列图形中的全等图形.
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
19.如图,已知,用尺规作图作,使.不写作法,但要保留作图痕迹.
20.在下列3个的网格中,画有正方形,沿网格线把正方形分分割成两个全等图形,请用三种不同的方法分割,画出分割线.
21.如图,,请写出图中的对应角,对应边.
①的对应角为( );②的对应角为( );③的对应角为( );④的对应边为( );⑤的对应边为( ).
22.如图所示,AE与BD相交于点C,∠A=∠E,AB=ED,求证:△ABC≌△EDC.
23.如图,AD是△ABC的高线,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD.求证:AD=BD.
24.如图,在△ABC中,,△ABC的角平分线、相交于点O,求证:.
25.如图,在△ABC中,,D为边上一点,平分,且,若,,求的长.
26.如图,在△ABC中,,点D,E分别在边上,连接交于点F,.
(1)说明:;
(2)若平分,,求△BEF的面积;
(3)判断之间的数量关系,并加以说明.
参考答案:
1.C
2.B
3.B
4.C
5.B
6.B
7.C
8.C
9.65°/65度
10.0.5<AD<3.5.
11.或或(答案不唯一)
12.
13.3
14.或
15.①②③④
16.∠2 △EDC 35米
17.或
18.(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形
19.解:作出的如图所示:
即为所求.
20.
21.,,,,
22.证明:在△ABC和△EDC中,
∵
∴△ABC≌△EDC(AAS) .
23.证明:∵AD是△ABC的高线,,
∴
∵BF=AC,FD=CD,
∴Rt△BDF≌Rt△ADC(HL),
∴AD=BD.
24.根据三角形内角和定理和角平分线的定义,得到,,在上截取,连接,分别证明△AOE≌△AOF(SAS),△COD≌△COF(ASA),得到,即可证明结论.
25.7
26.(1)证明:∵,
又∵,
∴,
∴;
(2)解:过点F作于点G,如图所示:
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵平分,,
∴,
∴;
(3)解:;理由如下:
在上截取,连接,如图所示:
在△ABH和△CAE中,
,
∴△ABH≌△CAE(SAS)
∴,
∴,
根据解析(2)可知,,
∴,
∴,
∴,
∴.
一、单选题
1.下列图形中,与已知图形全等的是( )
A. B. C. D.
2.下列说法不正确的是( )
A.三边分别相等的两个三角形全等
B.有两边及一角对应相等的两个三角形全等
C.有两角及一边对应相等的两个三角形全等
D.斜边和一条直角边分别相等的两个直角三角形全等
3.在△ABC中,∠C=90°,D为AB的中点,ED⊥AB,∠DAE=∠CAE,则 ∠CAB=( )
A.30° B.60° C.80 ° D.50°
4.如图,△ABC中,N是BC边上的中点,AM平分∠BAC,BM⊥AM于点M,若AB=8,MN=2.则AC的长为( )
A.10 B.11 C.12 D.13
5.如图,已知,在下列条件:①;②;③;④中,只补充一个就一定可以判断的条件是( )
A.①②③④ B.①②③ C.②③④ D.①②④
6.如图,已知△ABC的周长是42,分别平分和,于D,且,则△ABC的面积为( )
A.126 B.63 C.42 D.21
7.如图,某三角形材料断裂成Ⅰ、Ⅱ、Ⅲ三块,现要配置与原材料全等的三角形材料,应该利用材料Ⅲ,这样做利用的是三角形全等判定方法中的( )
A.边角边 B.角角边 C.角边角 D.边边边
8.如图,三条笔直公路两两相交,交点分别为,,,现计划修一个油库,要求到三条公路的距离都相等,△ABC内部被河水填满无法施工,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
二、填空题
9.如图,,若,则的度数为 .
10.在ABC中,AB=3,AC=4,则BC边上的中线AD的取值范围是
11.如图,,分别是上的点,要使,则还需添加的条件是 .(只需填写一个合适的条件即可,图中不能再添加其他点或线)
12.在如图所示的3×3正方形网格中, 度.
13.如图,在中,,平分交于点D,若,.则的长为 .
14.若两个三角形的两边和其中一边上的高分别相等,且其中一个三角形的第三边所对的角为,则另一个三角形的第三边所对的角为
15.如图△ABC中,,分别作△ABC的两个内角平分线和,、相交于点,连接,有以下结论:①;②平分;③;④,其中正确的结论有 .
16.如图,要测量河两岸相对的两点A、B的距离,在AB的垂线BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,则∠ABC=∠CDE=,BC=CD,∠1= ,所以△ABC≌ ,若测得的长为35米,则长为 .
17.已知:△ABC中,,,为射线上一动点,连接,在直线右侧作,且.连接交直线于,若,则的值为 .
三、解答题
18.找出下列图形中的全等图形.
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
19.如图,已知,用尺规作图作,使.不写作法,但要保留作图痕迹.
20.在下列3个的网格中,画有正方形,沿网格线把正方形分分割成两个全等图形,请用三种不同的方法分割,画出分割线.
21.如图,,请写出图中的对应角,对应边.
①的对应角为( );②的对应角为( );③的对应角为( );④的对应边为( );⑤的对应边为( ).
22.如图所示,AE与BD相交于点C,∠A=∠E,AB=ED,求证:△ABC≌△EDC.
23.如图,AD是△ABC的高线,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD.求证:AD=BD.
24.如图,在△ABC中,,△ABC的角平分线、相交于点O,求证:.
25.如图,在△ABC中,,D为边上一点,平分,且,若,,求的长.
26.如图,在△ABC中,,点D,E分别在边上,连接交于点F,.
(1)说明:;
(2)若平分,,求△BEF的面积;
(3)判断之间的数量关系,并加以说明.
参考答案:
1.C
2.B
3.B
4.C
5.B
6.B
7.C
8.C
9.65°/65度
10.0.5<AD<3.5.
11.或或(答案不唯一)
12.
13.3
14.或
15.①②③④
16.∠2 △EDC 35米
17.或
18.(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形
19.解:作出的如图所示:
即为所求.
20.
21.,,,,
22.证明:在△ABC和△EDC中,
∵
∴△ABC≌△EDC(AAS) .
23.证明:∵AD是△ABC的高线,,
∴
∵BF=AC,FD=CD,
∴Rt△BDF≌Rt△ADC(HL),
∴AD=BD.
24.根据三角形内角和定理和角平分线的定义,得到,,在上截取,连接,分别证明△AOE≌△AOF(SAS),△COD≌△COF(ASA),得到,即可证明结论.
25.7
26.(1)证明:∵,
又∵,
∴,
∴;
(2)解:过点F作于点G,如图所示:
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵平分,,
∴,
∴;
(3)解:;理由如下:
在上截取,连接,如图所示:
在△ABH和△CAE中,
,
∴△ABH≌△CAE(SAS)
∴,
∴,
根据解析(2)可知,,
∴,
∴,
∴,
∴.
