2.1.1直线的倾斜角与斜率 课件(共15张PPT)
文档属性
| 名称 | 2.1.1直线的倾斜角与斜率 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 975.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 06:29:00 | ||
图片预览





文档简介
(共15张PPT)
2.1.1直线的倾斜角与斜率
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法。
从本节开始,我们要学习一门全新的数学分支学科— 解析几何。
解析几何是17世纪法国数学家笛卡儿和费马创立的,它的基本内涵
和方法是:通过坐标系,把几何的基本元素--点和代数的基本对象
数(有序数对或数组)对应起来.
在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为
代数问题,再通过代数方法研究几何图形的性质.
解析几何的创立是数学发展史上的一个里程碑,数学从此进入
变量数学时期,它为微积分的创建奠定了基础.
坐标法是解析几何中最基本的研究方法.
数学史
一、导入新课
请同学们观察图片,说说图片中的直线有什么区别?
思考:在平面直角坐标系中,如何确定一条直线的位置?
两点可以确定一条直线
在平面直角坐标系中,由一点能否确定一条直线?
不能
直线的方向不同,相对于x轴的倾斜程度不同
这些直线都过点P,它们之间有什么区别?
二、讲授新课
二、讲授新课
问题1: 如何表示直线的方向?
1.不同的方向(倾斜程度)必须是相对于同一个参照物而言的.怎样借助直角坐标系刻画直线的方向呢
2.以x轴为“基准”,当直线l 与x轴相交时形成了四个角,我们用其中哪个角表示直线的“倾斜程度”
二、讲授新课
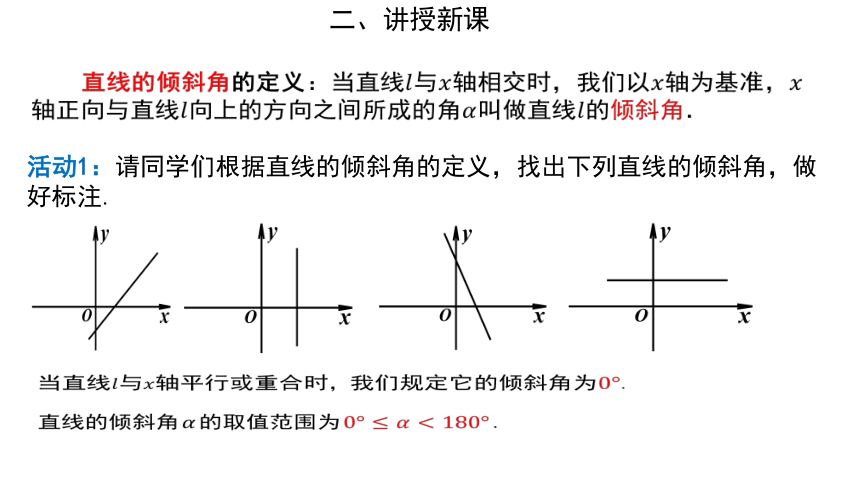
活动1:请同学们根据直线的倾斜角的定义,找出下列直线的倾斜角,做好标注.
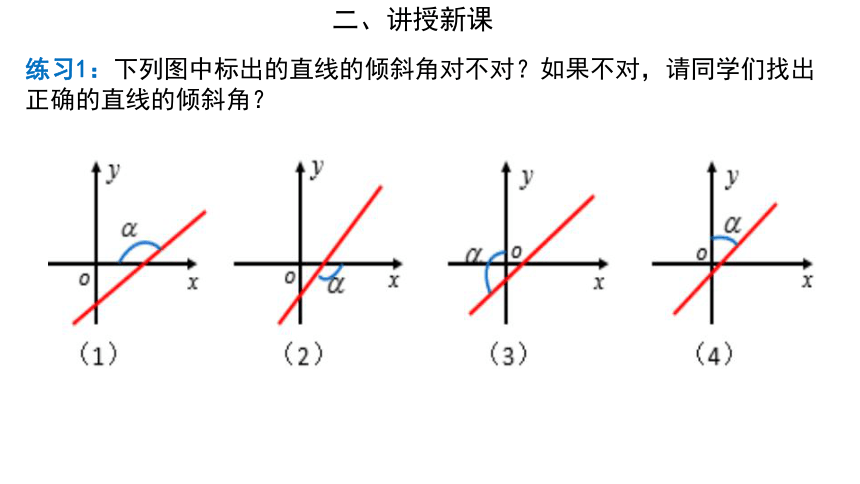
练习1:下列图中标出的直线的倾斜角对不对?如果不对,请同学们找出正确的直线的倾斜角?
二、讲授新课
直线OP的倾斜角为α.
由正切函数的定义,有
二、讲授新课
向量
直线OP的倾斜角为α.
向量
P的坐标为
P的坐标为(x2-x1,y2-y1)
直线OP的倾斜角为α
向量
结论: 直线l的倾斜角α与直线l上的两点P1(x1,y1),P2(x2,y2)(x1 x2)的坐标有如下关系:
直线的斜率:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tanα
练习2:课本55.练习123
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
例题讲解
图示
倾斜角(范围) α=0° 0°<α<90° α=_____ 90°<α<180°
斜率(范围) 0 (0,+∞) 不存在 (-∞,0)
四、课堂小结
(1)直线的倾斜角的定义以及如何找直线的倾斜角.
(2)直线的斜率.
(3)直线的倾斜角,斜率,直线上两点坐标之间的关系.
2.1.1直线的倾斜角与斜率
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法。
从本节开始,我们要学习一门全新的数学分支学科— 解析几何。
解析几何是17世纪法国数学家笛卡儿和费马创立的,它的基本内涵
和方法是:通过坐标系,把几何的基本元素--点和代数的基本对象
数(有序数对或数组)对应起来.
在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为
代数问题,再通过代数方法研究几何图形的性质.
解析几何的创立是数学发展史上的一个里程碑,数学从此进入
变量数学时期,它为微积分的创建奠定了基础.
坐标法是解析几何中最基本的研究方法.
数学史
一、导入新课
请同学们观察图片,说说图片中的直线有什么区别?
思考:在平面直角坐标系中,如何确定一条直线的位置?
两点可以确定一条直线
在平面直角坐标系中,由一点能否确定一条直线?
不能
直线的方向不同,相对于x轴的倾斜程度不同
这些直线都过点P,它们之间有什么区别?
二、讲授新课
二、讲授新课
问题1: 如何表示直线的方向?
1.不同的方向(倾斜程度)必须是相对于同一个参照物而言的.怎样借助直角坐标系刻画直线的方向呢
2.以x轴为“基准”,当直线l 与x轴相交时形成了四个角,我们用其中哪个角表示直线的“倾斜程度”
二、讲授新课
活动1:请同学们根据直线的倾斜角的定义,找出下列直线的倾斜角,做好标注.
练习1:下列图中标出的直线的倾斜角对不对?如果不对,请同学们找出正确的直线的倾斜角?
二、讲授新课
直线OP的倾斜角为α.
由正切函数的定义,有
二、讲授新课
向量
直线OP的倾斜角为α.
向量
P的坐标为
P的坐标为(x2-x1,y2-y1)
直线OP的倾斜角为α
向量
结论: 直线l的倾斜角α与直线l上的两点P1(x1,y1),P2(x2,y2)(x1 x2)的坐标有如下关系:
直线的斜率:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tanα
练习2:课本55.练习123
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
例题讲解
图示
倾斜角(范围) α=0° 0°<α<90° α=_____ 90°<α<180°
斜率(范围) 0 (0,+∞) 不存在 (-∞,0)
四、课堂小结
(1)直线的倾斜角的定义以及如何找直线的倾斜角.
(2)直线的斜率.
(3)直线的倾斜角,斜率,直线上两点坐标之间的关系.
