5.4二次函数与一元二次方程(2)教学设计 苏科版数学九年级下册
文档属性
| 名称 | 5.4二次函数与一元二次方程(2)教学设计 苏科版数学九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 50.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 00:00:00 | ||
图片预览

文档简介
5.4二次函数与一元二次方程(2)
【教学目标】会利用二次函数图像中函数值为0的点的位置特征,采用缩小范围、初步逼近的方法,借助计算器求出一元二次方程的近似解,进一步体会一元二次方程与二次函数的关系;
【重点】含参二次函数图像与x轴位置关系的判断.
【难点】运用二分法、对称性求方程根的近似值;
【教学过程】
活动一、观察这个式子,你能想到什么?
x2+2x-5=0
这是一个一元二次方程,还能想到二次函数y=x2+2x-5,并且函数图像与x轴公共点的横坐标就是一元二次方程的根.
请大家画出函数图像,通过观察函数图像,你能看出一元二次方程根的具体值是多少吗?
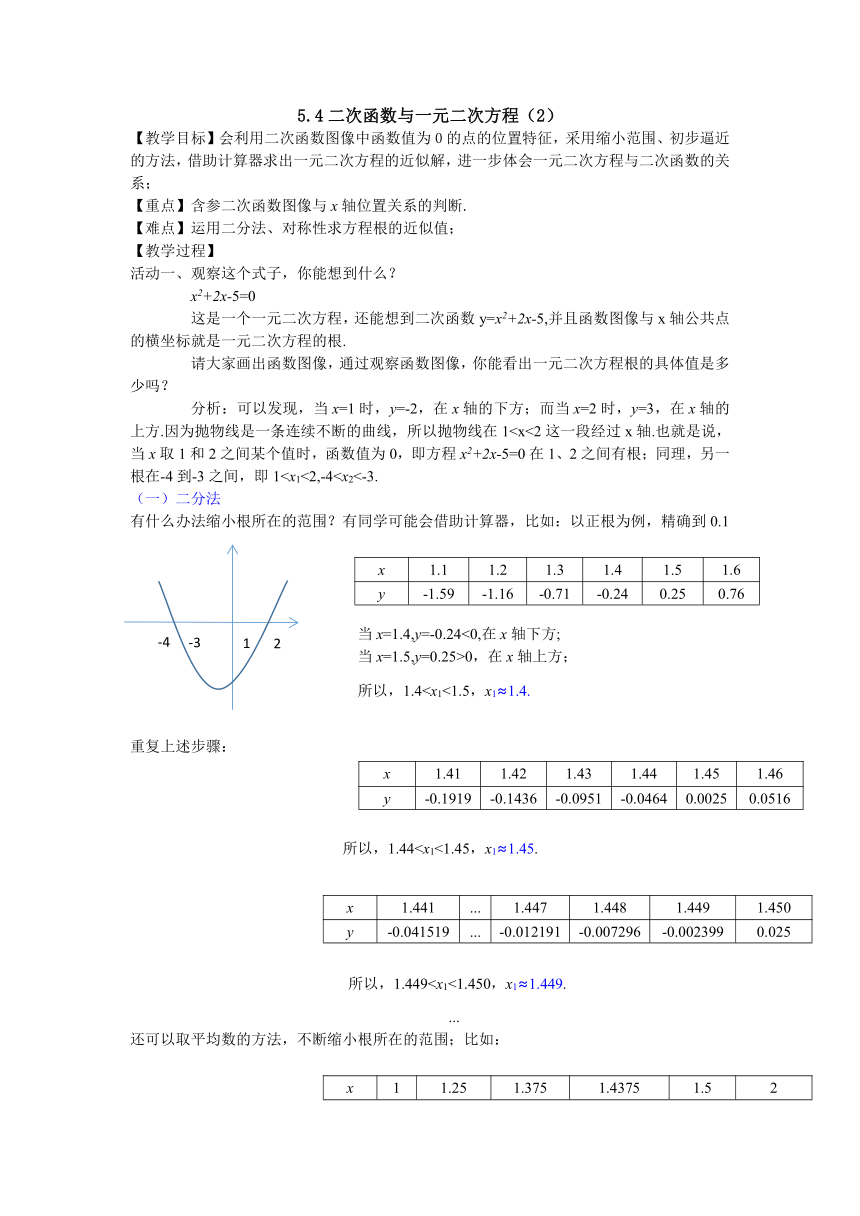
分析:可以发现,当x=1时,y=-2,在x轴的下方;而当x=2时,y=3,在x轴的上方.因为抛物线是一条连续不断的曲线,所以抛物线在1(一)二分法
有什么办法缩小根所在的范围?有同学可能会借助计算器,比如:以正根为例,精确到0.1
x 1.1 1.2 1.3 1.4 1.5 1.6
y -1.59 -1.16 -0.71 -0.24 0.25 0.76
当x=1.4,y=-0.24<0,在x轴下方;
当x=1.5,y=0.25>0,在x轴上方;
所以,1.4重复上述步骤:
x 1.41 1.42 1.43 1.44 1.45 1.46
y -0.1919 -0.1436 -0.0951 -0.0464 0.0025 0.0516
所以,1.44x 1.441 ... 1.447 1.448 1.449 1.450
y -0.041519 ... -0.012191 -0.007296 -0.002399 0.025
所以,1.449...
还可以取平均数的方法,不断缩小根所在的范围;比如:
x 1 1.25 1.375 1.4375 1.5 2
y -2 -0.9375 -0.359375 -0.05859375 0.25 4
x=(1+2)/2=1.5 ,y=0.25,所以1x=(1+1.5)/2=1.25 ,y=-0.9375,所以1.25x=(1.25+1.5)/2=1.375 ,y=-0.359375,所以1.375x=(1.375+1.5)/2=1.475 ,y=-0.05859375,所以1.4375可以看到根所在范围越来越小,根所在范围的两端的值越来越接近根的值,因而可以作为根的近似值.
因为|1.4375-1.5|=0.0625<0.1,所以x1≈1.4375.
因为这种方法是通过不断的取平均数进行估计的,因而称为二分法.
问:你能不能选择以上两种方法中的任意一种来确定方程x2+2x-5=0另一个根的近似值?如果你会,动笔写写.
x -4 -3.5 -3.4375 -3.375 -3.25 -3
y 3 0.25 -0.05859375 -0.359375 -0.9375 -2
因为-3.5-(-3.4375)|=0.0625<0.1,所以x2≈-3.4375.
还有其他方法吗?可不可以根据对称性求呢?
对称性
对称轴:直线x=-1,x1≈1.4375,因为对称点到对称轴的距离相等,所以以求得x2≈-3.4375.
之前都是利用二次函数图像求对应的一元二次方程根的值,换个角度看方程x2+2x-5=0,你还能想到其它函数吗?
x2+2x-5=0
在同一坐标轴里画出这两个函数的图像,于是这两个函数的公共点的横坐标就是一元二次方程的根;
x2=-2x+5
二次函数 一次函数 得:1y=x2 y=-2x+5
例题讲解
例 已知二次函数y=x2-2x-2的部分值如下表,结合前面的经验你能确定一元二次函数x2-2x-2=0的根的近似值吗?(精确到0.01)
x 2.71 2.72 2.73 2.74 2.75 2.76
y -0.0759 -0.0416 -0.0071 0.0276 0.0625 0.0976
分析:(1)图像:可以先画出图像,发现其中一个根在-1~0之间,另一个根在2~3之间,要想得到精确的值,需要回到表格之中去.观察发现:当x=2.73时,y=-0.0071<0;当x=2.74时,y=0.0276>0,所以方程的一个根在2,73~2.74之间;因为|-0.0071|<|0.0276|,所以x1≈2.73.
思考:另一个根怎么确定?(可以根据前面所学的对称性来解决)
分析:(2)对称性:根据对称点到对称轴的距离相等,
因为对称轴为直线x=1,所以x2≈-0.73.
利用图像和对称性求根的近似值的这两种方法也适用于更高次的一元方程(引出活动二)
活动二、利用函数图像,探索方程的根的取值范围.
函数:y=2x3+3x2-12x+3
方程:2x3+3x2-12x+3=0
分析:根据前面的研究,我们应该积累了一个经验,就是应该观察这个函数图像与x轴的公共点的位置;
(1)观察发现,这个函数图像与x轴共有三个公共点.那么这个方程根的情况应该如何判断?
观察图像发现-4还能更精确吗?
还能看到其他熟悉的函数吗?
2x3+3x2-12x+3=0
2x2+3x-12+3/x=0
2x2+3x-12=-3/x
二次函数 反比例函数
y=2x2+3x-12 y=-3/x
同学们可以在同一坐标系中画出这两个函数的图像,观察发现了什么?
发现:原方程的根为二次函数图像与反比例函数图像公共点的横坐标.
【教学目标】会利用二次函数图像中函数值为0的点的位置特征,采用缩小范围、初步逼近的方法,借助计算器求出一元二次方程的近似解,进一步体会一元二次方程与二次函数的关系;
【重点】含参二次函数图像与x轴位置关系的判断.
【难点】运用二分法、对称性求方程根的近似值;
【教学过程】
活动一、观察这个式子,你能想到什么?
x2+2x-5=0
这是一个一元二次方程,还能想到二次函数y=x2+2x-5,并且函数图像与x轴公共点的横坐标就是一元二次方程的根.
请大家画出函数图像,通过观察函数图像,你能看出一元二次方程根的具体值是多少吗?
分析:可以发现,当x=1时,y=-2,在x轴的下方;而当x=2时,y=3,在x轴的上方.因为抛物线是一条连续不断的曲线,所以抛物线在1
有什么办法缩小根所在的范围?有同学可能会借助计算器,比如:以正根为例,精确到0.1
x 1.1 1.2 1.3 1.4 1.5 1.6
y -1.59 -1.16 -0.71 -0.24 0.25 0.76
当x=1.4,y=-0.24<0,在x轴下方;
当x=1.5,y=0.25>0,在x轴上方;
所以,1.4
x 1.41 1.42 1.43 1.44 1.45 1.46
y -0.1919 -0.1436 -0.0951 -0.0464 0.0025 0.0516
所以,1.44
y -0.041519 ... -0.012191 -0.007296 -0.002399 0.025
所以,1.449
还可以取平均数的方法,不断缩小根所在的范围;比如:
x 1 1.25 1.375 1.4375 1.5 2
y -2 -0.9375 -0.359375 -0.05859375 0.25 4
x=(1+2)/2=1.5 ,y=0.25,所以1
因为|1.4375-1.5|=0.0625<0.1,所以x1≈1.4375.
因为这种方法是通过不断的取平均数进行估计的,因而称为二分法.
问:你能不能选择以上两种方法中的任意一种来确定方程x2+2x-5=0另一个根的近似值?如果你会,动笔写写.
x -4 -3.5 -3.4375 -3.375 -3.25 -3
y 3 0.25 -0.05859375 -0.359375 -0.9375 -2
因为-3.5-(-3.4375)|=0.0625<0.1,所以x2≈-3.4375.
还有其他方法吗?可不可以根据对称性求呢?
对称性
对称轴:直线x=-1,x1≈1.4375,因为对称点到对称轴的距离相等,所以以求得x2≈-3.4375.
之前都是利用二次函数图像求对应的一元二次方程根的值,换个角度看方程x2+2x-5=0,你还能想到其它函数吗?
x2+2x-5=0
在同一坐标轴里画出这两个函数的图像,于是这两个函数的公共点的横坐标就是一元二次方程的根;
x2=-2x+5
二次函数 一次函数 得:1
例题讲解
例 已知二次函数y=x2-2x-2的部分值如下表,结合前面的经验你能确定一元二次函数x2-2x-2=0的根的近似值吗?(精确到0.01)
x 2.71 2.72 2.73 2.74 2.75 2.76
y -0.0759 -0.0416 -0.0071 0.0276 0.0625 0.0976
分析:(1)图像:可以先画出图像,发现其中一个根在-1~0之间,另一个根在2~3之间,要想得到精确的值,需要回到表格之中去.观察发现:当x=2.73时,y=-0.0071<0;当x=2.74时,y=0.0276>0,所以方程的一个根在2,73~2.74之间;因为|-0.0071|<|0.0276|,所以x1≈2.73.
思考:另一个根怎么确定?(可以根据前面所学的对称性来解决)
分析:(2)对称性:根据对称点到对称轴的距离相等,
因为对称轴为直线x=1,所以x2≈-0.73.
利用图像和对称性求根的近似值的这两种方法也适用于更高次的一元方程(引出活动二)
活动二、利用函数图像,探索方程的根的取值范围.
函数:y=2x3+3x2-12x+3
方程:2x3+3x2-12x+3=0
分析:根据前面的研究,我们应该积累了一个经验,就是应该观察这个函数图像与x轴的公共点的位置;
(1)观察发现,这个函数图像与x轴共有三个公共点.那么这个方程根的情况应该如何判断?
观察图像发现-4
还能看到其他熟悉的函数吗?
2x3+3x2-12x+3=0
2x2+3x-12+3/x=0
2x2+3x-12=-3/x
二次函数 反比例函数
y=2x2+3x-12 y=-3/x
同学们可以在同一坐标系中画出这两个函数的图像,观察发现了什么?
发现:原方程的根为二次函数图像与反比例函数图像公共点的横坐标.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
