6.2方差课件1
图片预览






文档简介
课件19张PPT。湘教版七年级下册6.2 方差
有两个女声合唱队,各由5名队员组成,她们的身高为(单位:厘米):
甲队:160,162,159,160,159
乙队:180,160,150,150,160.如果单从队员的身高考虑,哪队的演出效果好?不难算出每个队的平均身高都是160厘米,但甲队身高波动小,乙队身高波动大,单从身高考虑,甲队比较整齐,演出的效果会好一些.
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的分散程度.
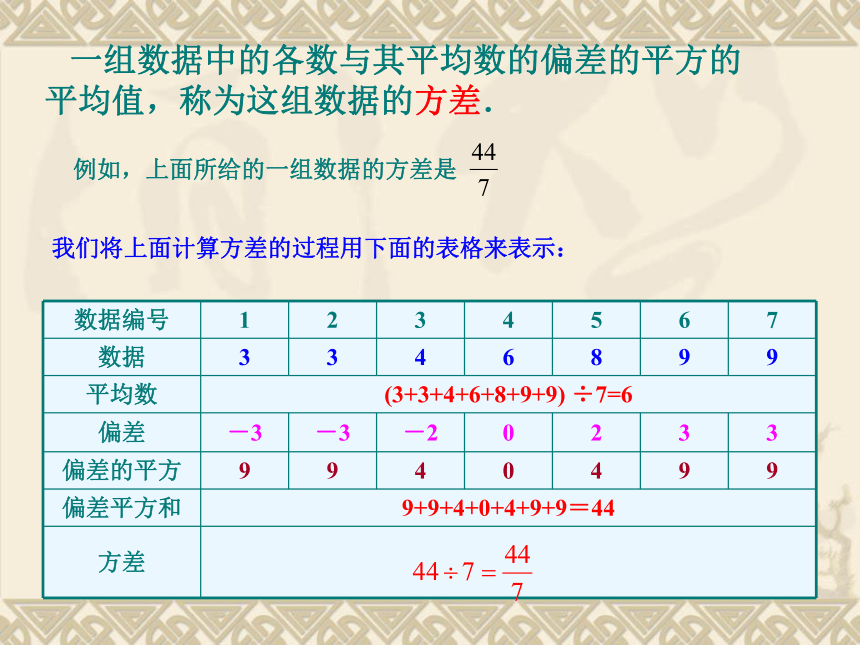
如何反映一组数据与其平均数的偏离程度?给定一组数据:3,3,4,6,8,9,9,其平均数是这组数据中的每个数与平均数6的偏差是:将各个数与平均数的偏差相加,能否得到总偏差?你用什么方法可以反映总偏差的大小?可以考虑先取绝对值再相加. 一组数据中的各数与其平均数的偏差的平方的平均值,称为这组数据的方差.例如,上面所给的一组数据的方差是我们将上面计算方差的过程用下面的表格来表示: 计算前面的实例中甲、乙两个女声合唱队各队队员身高的方差,并说明计算结果的实际意义.乙队队员身高的方差是: 计算的结果表明:乙队队员身高的方差比甲队队员身高的方差大得多,即乙队中各队员的身高与她们的平均身高的偏差大,而甲队中各队员的身高与她们的平均身高的偏差小,这说明乙队的队员高的高,矮的矮而甲队队员的身高比较整齐.解甲、乙两队中,每队队员的平均身高都是160厘米,甲队队员身高的方差是:方差反映的是一组数据哪个方面的特征?5名女篮球队员的身高为(单位:厘米)
193 182 187 174 189
试求出这组数据的方差,并说明其具体含义.方差是每个队员的身高与她们的平均身高的偏差的平方的平均值,它涉及数据组中的每个数据,反映了数据组与其平均数的偏离程度.平均身高:方差:解1.一个小组有8名同学,分别测量同一根绳子的长度,测得的数据如下(单位:厘米)
108.5, 110, 109.3 108.9
110.8 110.5 109.4 109.2
(1)如何确定这根绳子的长度的近似值?
(2)如何评价测量结果的准确程度?2.一组数据的方差为0,这组数据有什么特点?方差可以是负数吗?为什么?一组数据的平均数表示这组数据的一般水平或数据的集中位置,一组数据的方差是各数据相对于它们的平均数的偏差的平方的平均数,方差的意义在于:它反映了一组数据的分散或波动的程度. 棉花纤维的平均长度是评价棉花质量的一个重要指标,但不是唯一的指标.纤维越长的棉花纺成棉纱质量越好,用来制成的棉织制品的质量也越好.但如果一批棉花的纤维长的长、短的短,参差不齐,并不是好棉花,反之,纤维长度比较均匀、整齐,才是质量好的棉花,棉花纤维的长度是否均匀,可以用方差来反映:方差越小,各种长度的纤维之间差别越小,棉花的质量越好.和纤维的平均长度一样,方差也是评价一批棉花质量的重要指标.质 量 评 估如何评价一批棉花的质量?用加权平均计算棉花纤维长度的平均数:用加权平均计算棉花纤维的方差:答:这批棉花纤维的平均长度为4.85厘米,其方差为1.3275厘米2有一批棉花,其各种长度的纤维所占比例如表所示:试求这批棉花纤维的平均长度与方差.解 一台机床生产一种圆柱形零件,按设计要求,圆柱的直径为40毫米.由于生产条件的限制和一些不确定的因素的影响,生产出来的每个零件的直径不可能恰好都是40毫米,而是在40毫米的上、下波动.显然,在正常生产的条件下,这种波动的程度不能太大,以保证零件的直径合乎设计要求.生产过程的控制 我们知道,数据的波动程度可以通过方差来反映,为了保证生产正常,我们可以通过测量产品直径的方差对生产过程进行监控:例如,每隔一段时间从这段时间生产的产品中任意地取出10件,测量它们的直径得到一组数据,计算出这组数据的方差,如果方差不超过预定的数量,则认为生产正常;否则,应对生产过程进行调整以恢复正常,保证产品质量. 对于我们的问题,根据以往的经验,在正常生产时直径的方差应不超过0.01毫米2,下表是某日8:30—9:30及10:00—11:00两个时段中各任意抽取10件产品量出的直径的数值(单位:毫米):用计算器可以算出两组数据的平均数都是40(毫米),能否根据平均长度等于设计长度就判断生产正常呢?如何对生产情况作出评价?虽然产品直径的平均长度等于设计长度,但每件产品的直径还是可能在平均数的上、下波动,偏离平均数,所以还应该进一步考察方差,以了解数据波动的情况.8:30—9:30生产的10件产品的直径的方差是0.026,远远超过0.01的界限,故生产情况不正常;经过调整后,在10:00—11:00生产的10件产品的直径的方差为0.008,已控制在0.01的范围内,说明生产过程已恢复正常.1.某企业对员工的工资情况进行调查,他们将月工资分为800元、1000元、1500元三个等级,每个等级职工人数占职工总数的比例分别为 , 试求这个单位职工月工资的平均数及方差,并说明其涵义.2.甲、乙两个城市的月平均气温如下表示(单位:℃)试求甲、乙两地月平均气温的方差.并对两地气温变化情况作出比较.
有两个女声合唱队,各由5名队员组成,她们的身高为(单位:厘米):
甲队:160,162,159,160,159
乙队:180,160,150,150,160.如果单从队员的身高考虑,哪队的演出效果好?不难算出每个队的平均身高都是160厘米,但甲队身高波动小,乙队身高波动大,单从身高考虑,甲队比较整齐,演出的效果会好一些.
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的分散程度.
如何反映一组数据与其平均数的偏离程度?给定一组数据:3,3,4,6,8,9,9,其平均数是这组数据中的每个数与平均数6的偏差是:将各个数与平均数的偏差相加,能否得到总偏差?你用什么方法可以反映总偏差的大小?可以考虑先取绝对值再相加. 一组数据中的各数与其平均数的偏差的平方的平均值,称为这组数据的方差.例如,上面所给的一组数据的方差是我们将上面计算方差的过程用下面的表格来表示: 计算前面的实例中甲、乙两个女声合唱队各队队员身高的方差,并说明计算结果的实际意义.乙队队员身高的方差是: 计算的结果表明:乙队队员身高的方差比甲队队员身高的方差大得多,即乙队中各队员的身高与她们的平均身高的偏差大,而甲队中各队员的身高与她们的平均身高的偏差小,这说明乙队的队员高的高,矮的矮而甲队队员的身高比较整齐.解甲、乙两队中,每队队员的平均身高都是160厘米,甲队队员身高的方差是:方差反映的是一组数据哪个方面的特征?5名女篮球队员的身高为(单位:厘米)
193 182 187 174 189
试求出这组数据的方差,并说明其具体含义.方差是每个队员的身高与她们的平均身高的偏差的平方的平均值,它涉及数据组中的每个数据,反映了数据组与其平均数的偏离程度.平均身高:方差:解1.一个小组有8名同学,分别测量同一根绳子的长度,测得的数据如下(单位:厘米)
108.5, 110, 109.3 108.9
110.8 110.5 109.4 109.2
(1)如何确定这根绳子的长度的近似值?
(2)如何评价测量结果的准确程度?2.一组数据的方差为0,这组数据有什么特点?方差可以是负数吗?为什么?一组数据的平均数表示这组数据的一般水平或数据的集中位置,一组数据的方差是各数据相对于它们的平均数的偏差的平方的平均数,方差的意义在于:它反映了一组数据的分散或波动的程度. 棉花纤维的平均长度是评价棉花质量的一个重要指标,但不是唯一的指标.纤维越长的棉花纺成棉纱质量越好,用来制成的棉织制品的质量也越好.但如果一批棉花的纤维长的长、短的短,参差不齐,并不是好棉花,反之,纤维长度比较均匀、整齐,才是质量好的棉花,棉花纤维的长度是否均匀,可以用方差来反映:方差越小,各种长度的纤维之间差别越小,棉花的质量越好.和纤维的平均长度一样,方差也是评价一批棉花质量的重要指标.质 量 评 估如何评价一批棉花的质量?用加权平均计算棉花纤维长度的平均数:用加权平均计算棉花纤维的方差:答:这批棉花纤维的平均长度为4.85厘米,其方差为1.3275厘米2有一批棉花,其各种长度的纤维所占比例如表所示:试求这批棉花纤维的平均长度与方差.解 一台机床生产一种圆柱形零件,按设计要求,圆柱的直径为40毫米.由于生产条件的限制和一些不确定的因素的影响,生产出来的每个零件的直径不可能恰好都是40毫米,而是在40毫米的上、下波动.显然,在正常生产的条件下,这种波动的程度不能太大,以保证零件的直径合乎设计要求.生产过程的控制 我们知道,数据的波动程度可以通过方差来反映,为了保证生产正常,我们可以通过测量产品直径的方差对生产过程进行监控:例如,每隔一段时间从这段时间生产的产品中任意地取出10件,测量它们的直径得到一组数据,计算出这组数据的方差,如果方差不超过预定的数量,则认为生产正常;否则,应对生产过程进行调整以恢复正常,保证产品质量. 对于我们的问题,根据以往的经验,在正常生产时直径的方差应不超过0.01毫米2,下表是某日8:30—9:30及10:00—11:00两个时段中各任意抽取10件产品量出的直径的数值(单位:毫米):用计算器可以算出两组数据的平均数都是40(毫米),能否根据平均长度等于设计长度就判断生产正常呢?如何对生产情况作出评价?虽然产品直径的平均长度等于设计长度,但每件产品的直径还是可能在平均数的上、下波动,偏离平均数,所以还应该进一步考察方差,以了解数据波动的情况.8:30—9:30生产的10件产品的直径的方差是0.026,远远超过0.01的界限,故生产情况不正常;经过调整后,在10:00—11:00生产的10件产品的直径的方差为0.008,已控制在0.01的范围内,说明生产过程已恢复正常.1.某企业对员工的工资情况进行调查,他们将月工资分为800元、1000元、1500元三个等级,每个等级职工人数占职工总数的比例分别为 , 试求这个单位职工月工资的平均数及方差,并说明其涵义.2.甲、乙两个城市的月平均气温如下表示(单位:℃)试求甲、乙两地月平均气温的方差.并对两地气温变化情况作出比较.
