5.3 图形变换的简单应用课件2
图片预览








文档简介
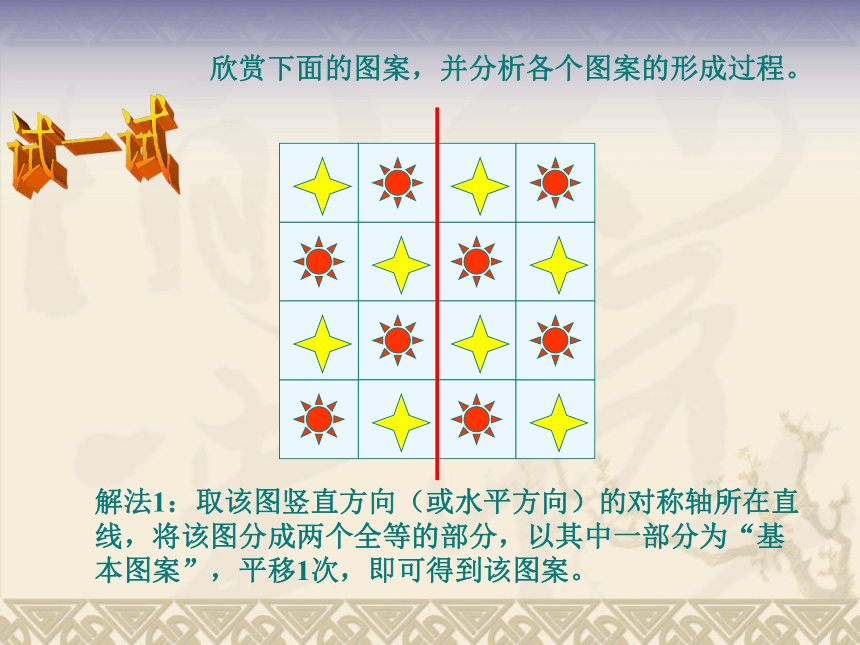
课件24张PPT。5.3图形变换的简单应用 :由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫轴反射. :由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫 做图形的平移变换,简称平移。 :由一图形变为另一图形,在改变的过程中,原图形上的所有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形改变叫做图形的旋转变换,简称旋转.这个定点称为旋转中心,转动的角称为旋转角轴对称变换平移变换旋转变换1、我们学过哪些图形变换?2、轴对称变换、平移变换、旋转变换的性质?轴对称变换:①由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全一样。②新图形上的每一点,都是原图形上的某一点关于直线L的对称点。③成轴对称的两个图形中,连接任意一对对应点的线段被对称轴垂直平分。平移:①平移是指整个图形平行移动,包括图形的每一条线段,每一个点. ②平移不改变图形的形状、大小,只改变图形的位置.③经过平移,对应线段、对应角分别相等,新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连结各组对应点的线段平行且相等。旋转:①对应点到旋转中心的距离相等.②各组对应点与旋转中心的连线所成的角相等,都等于旋转角。③旋转中心是唯一不动的点④旋转不改变图形的大小和形状.变换方法?基本图案?平移旋转对称轴位置对称轴条数平移方向平移距离平移次数旋转中心旋转方向旋转角度旋转次数轴对称探究方向 观察下列图案,说出它们分别是由那个基础图形经过怎样的变换得到的,在图中吧基础图形标出来(或把基础图形画出来)。一、会看可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880欣赏下面的图案,并分析各个图案的形成过程。解法1:取该图竖直方向(或水平方向)的对称轴所在直线,将该图分成两个全等的部分,以其中一部分为“基本图案”,平移1次,即可得到该图案。试一试欣赏下面的图案,并分析各个图案的形成过程。解法2:取该图竖直方向、水平方向的对称轴线将该图分成四个全等的部分,以左上角的这部分为“基本图案”,连续平移3次,即可得到该图案。欣赏下面的图案,并分析各个图案的形成过程。解法3:取该图竖直方向(或水平方向)的对称轴线将该图分成两个全等的部分,以其中的一部分为“基本图案”,以整个图案的中心为旋转中心,按逆(顺)时针方向旋转180°(1次),前后的图形共同组成该图案。欣赏下面的图案,并分析各个图案的形成过程。解法4:取该图中大正方形对角线所在的直线为对称轴,将该图分成两个相等的部分,以其中一部分为“基本图案”,作它关于对称轴的轴对称图形,即可得到该图案。 1、如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴。
整个图案是个什么形状?请准确地画出它的另一半。BACDEFGH二、会画2、试用两个等圆,两个全等三角形,两条平行且相等的线段设计一些具有平移、旋转和轴对称关系的图案,并说明你的设计意图。 试用两个等圆,两个全等三角形,两条平行且相等的线段设计一些具有平移、旋转和轴对称关系的图案,并说明你的设计意图。两盏电灯两支棒棒糖平移关系轴对称关系旋转关系错位倒置等价交换轴对称关系一个外星人一辆小车3、能够灵活运用平移变换、旋转变换、轴对称变换及它们的组合解决某些图形的计算、证明问题。(1)巧用移位思想,灵活求解面积例1:如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD例1:如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD解:图中阴影部分的面积是小路 例1如图,一块矩形草地,长为12米,宽为8米,其中有一条宽为2米的小路,你能猜出绿色部分表示的草地的面积吗?说说你的理由.128 如图,一块矩形草地,长为12米,宽为8米,其中有一条宽为2米的小路,你能猜出绿色部分表示的草地的面积吗?说说你的理由.128小路 如图,一块矩形草地,长为12米,宽为8米,其中有一条宽为2米的小路,你能猜出绿色部分表示的草地的面积吗?说说你的理由.128xiaojie如图所示,长方形花园ABCD,AD=a,AB=b,花园中修有两条小路(小路任何地方的水平宽度都是一个单位)。你能借助平移、旋转的方法求出图中种花部分的面积吗?说说你的做法。将“小路”沿左右上下各个边界“剪去”,将左侧的花地向右平移一个单位,将下面的花地向上平移一个单位,得到一个新的矩形,它的纵向宽是b-1,而水平方向的长变成了a-1,所以花地面积为(a-1)(b-1)=ab-a-b+1将纵向“小路” 绕点逆时针旋转“扶直”,再将“扶直”的“小路”向左平移到花地左边,将横向“小路”向上平移到花地上边,得到一个新的矩形,它的纵向宽是b-1,而水平方向的长变成了a-1,所以草地面积为(a-1)(b-1)=ab-a-b+1ABA D
B C CaDb练一练A D
B C A D
B C 正方形ABCD中, E为BC上任一点,AF是∠DAE的平分线,交CD于点F,求证:AE=BE+FDDABCEF证明:E′将△ABE绕点O旋转90°得△ADE ,
BE=DE′,AE=AE′,∠4= ∠3
∵ AF是∠DAE的平分线(已知)
∴∠1= ∠2(角平分线的定义)
∴∠1 +∠4= ∠2+ ∠3即∠BAF= ∠FAE′
又∵AB∥CD(正方形性质)
∴ ∠BAF= ∠5(两直线平行,内错角相等)
∴ ∠FAE′= ∠5 (等量代换)
∴ AE′= FE′(等角对等边)
∴AE=BE+FD (等量代换)43125(2)利用轴对称,解决折叠问题小结 这节课通过对生活实际中的典型图案进行观察、分析、欣赏的过程,进一步发展空间观念,增强审美意识(会看) 。 认识和欣赏平移变换、旋转变换、轴对称变换在现实生活实际中的应用,学习运用平移变换、旋转变换、轴对称变换及它们的组合进行一定的图案设计(会画) 。应用平移变换、旋转变换、轴对称变换将那些分散、远离的条件从图形的某一部位转移到适当的新位置上,得以相对集中,从而达到化繁为简、化难为易、巧妙解题的目的。
整个图案是个什么形状?请准确地画出它的另一半。BACDEFGH二、会画2、试用两个等圆,两个全等三角形,两条平行且相等的线段设计一些具有平移、旋转和轴对称关系的图案,并说明你的设计意图。 试用两个等圆,两个全等三角形,两条平行且相等的线段设计一些具有平移、旋转和轴对称关系的图案,并说明你的设计意图。两盏电灯两支棒棒糖平移关系轴对称关系旋转关系错位倒置等价交换轴对称关系一个外星人一辆小车3、能够灵活运用平移变换、旋转变换、轴对称变换及它们的组合解决某些图形的计算、证明问题。(1)巧用移位思想,灵活求解面积例1:如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD例1:如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD解:图中阴影部分的面积是小路 例1如图,一块矩形草地,长为12米,宽为8米,其中有一条宽为2米的小路,你能猜出绿色部分表示的草地的面积吗?说说你的理由.128 如图,一块矩形草地,长为12米,宽为8米,其中有一条宽为2米的小路,你能猜出绿色部分表示的草地的面积吗?说说你的理由.128小路 如图,一块矩形草地,长为12米,宽为8米,其中有一条宽为2米的小路,你能猜出绿色部分表示的草地的面积吗?说说你的理由.128xiaojie如图所示,长方形花园ABCD,AD=a,AB=b,花园中修有两条小路(小路任何地方的水平宽度都是一个单位)。你能借助平移、旋转的方法求出图中种花部分的面积吗?说说你的做法。将“小路”沿左右上下各个边界“剪去”,将左侧的花地向右平移一个单位,将下面的花地向上平移一个单位,得到一个新的矩形,它的纵向宽是b-1,而水平方向的长变成了a-1,所以花地面积为(a-1)(b-1)=ab-a-b+1将纵向“小路” 绕点逆时针旋转“扶直”,再将“扶直”的“小路”向左平移到花地左边,将横向“小路”向上平移到花地上边,得到一个新的矩形,它的纵向宽是b-1,而水平方向的长变成了a-1,所以草地面积为(a-1)(b-1)=ab-a-b+1ABA D
B C CaDb练一练A D
B C A D
B C 正方形ABCD中, E为BC上任一点,AF是∠DAE的平分线,交CD于点F,求证:AE=BE+FDDABCEF证明:E′将△ABE绕点O旋转90°得△ADE ,
BE=DE′,AE=AE′,∠4= ∠3
∵ AF是∠DAE的平分线(已知)
∴∠1= ∠2(角平分线的定义)
∴∠1 +∠4= ∠2+ ∠3即∠BAF= ∠FAE′
又∵AB∥CD(正方形性质)
∴ ∠BAF= ∠5(两直线平行,内错角相等)
∴ ∠FAE′= ∠5 (等量代换)
∴ AE′= FE′(等角对等边)
∴AE=BE+FD (等量代换)43125(2)利用轴对称,解决折叠问题小结 这节课通过对生活实际中的典型图案进行观察、分析、欣赏的过程,进一步发展空间观念,增强审美意识(会看) 。 认识和欣赏平移变换、旋转变换、轴对称变换在现实生活实际中的应用,学习运用平移变换、旋转变换、轴对称变换及它们的组合进行一定的图案设计(会画) 。应用平移变换、旋转变换、轴对称变换将那些分散、远离的条件从图形的某一部位转移到适当的新位置上,得以相对集中,从而达到化繁为简、化难为易、巧妙解题的目的。
