24.1.4圆周角——圆周角定理及其推论 教案(表格式)初中数学人教版九年级上
文档属性
| 名称 | 24.1.4圆周角——圆周角定理及其推论 教案(表格式)初中数学人教版九年级上 |

|
|
| 格式 | docx | ||
| 文件大小 | 76.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 18:20:14 | ||
图片预览

文档简介
课题 24.1.4圆周角 第一课时 圆周角定理及其推论
上课教师 上课时间 第 周 第 节
教学 目标 1、理解圆周角的定义,会区分圆周角和圆心角。 2、掌握圆周角定理,并会用此定理进行简单的论证和计算。 3、在探索学习过程中增强自主学习独立思考能力,提升学习信心。
教学 重点 圆周角的定理、圆周角的定理的推导及运用它们解题
教学 难点 圆周角的定理、圆周角的定理的推导及运用它们解题
教 学 过 程
环节 教师活动 学生活动 设计意图
课前预习 1、布置学生的课前预习任务 2、进行预习方法指导 3、对学生预习任务的检查与评定。 1、认真阅读教材第85-86页内容,铅笔勾画重点概念 2、完成《新课程实践与探案丛书》(以后简称《练习册》)课堂练习69-70页例1、例2。 培养学生课前预习习惯,提升学生自主学习能力。
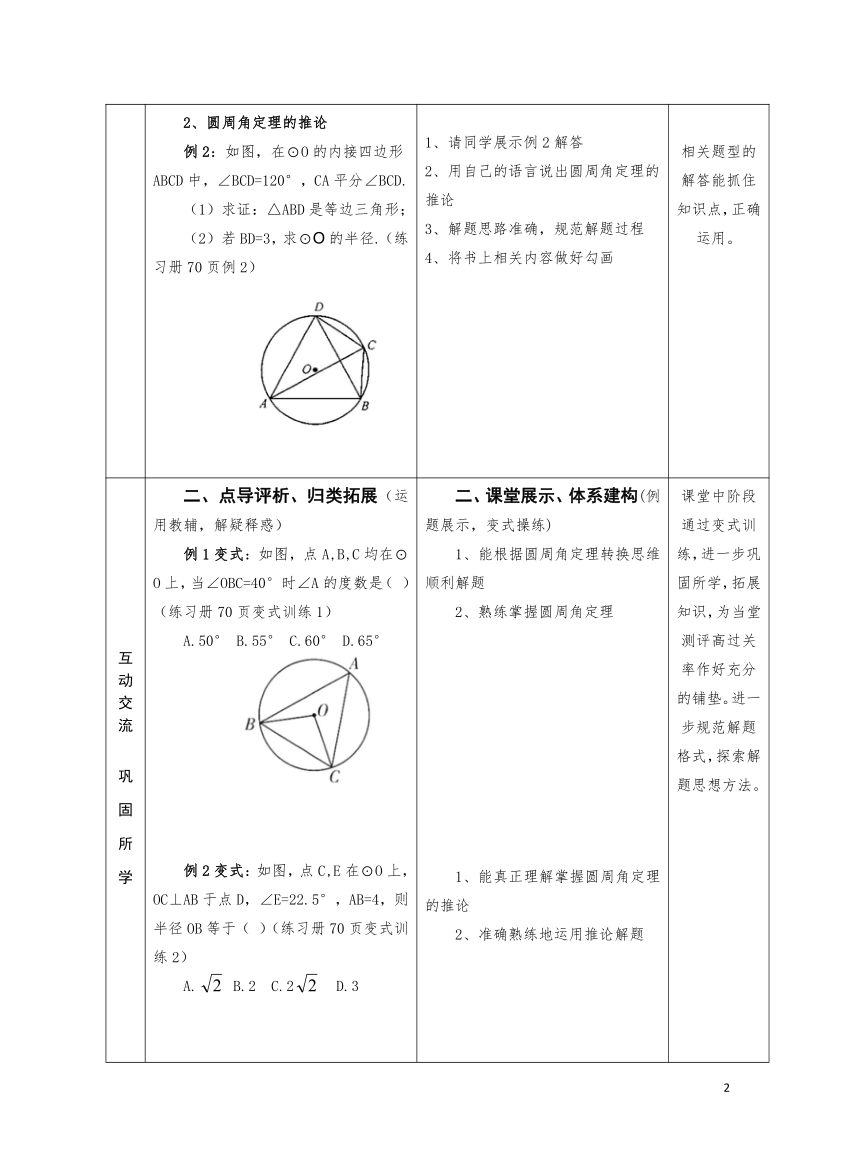
自主学习 理解新知 一、师生互动、引问激思(运用教材,梳理知识) 1、圆周角定义及定理 例1:如图,AB是⊙O的直径,C,D是⊙O上的两点,分别连接AC,BC,CD,OD.若∠DOB=140°,则∠ACD=( )(练习册69页例1) A.20° B.30° C.40° D.70° 2、圆周角定理的推论 例2:如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD. 求证:△ABD是等边三角形; 若BD=3,求⊙O的半径.(练习册70页例2) 一、进入情境、领会所学(理解教材,领悟新知) 1、请同学分享例1解答 2、说出圆周角的概念及用自己的语言表述圆周角定理(完成教材第85-86页内容的理解) 3、在书上将相关知识点进行勾画 1、请同学展示例2解答 2、用自己的语言说出圆周角定理的推论 3、解题思路准确,规范解题过程 4、将书上相关内容做好勾画 课堂前阶段通过课堂师生互动,学生初步领会本课核心内容。 从教材阅读对基本概念有初步认识,通过练习加强对基本概念的理解。 相关题型的解答能抓住知识点,正确运用。
互动交流 巩固所学 二、点导评析、归类拓展(运用教辅,解疑释惑) 例1变式:如图,点A,B,C均在⊙O上,当∠OBC=40°时∠A的度数是( )(练习册70页变式训练1) A.50° B.55° C.60° D.65° 例2变式:如图,点C,E在⊙O上,OC⊥AB于点D,∠E=22.5°,AB=4,则半径OB等于( )(练习册70页变式训练2) A. B.2 C.2 D.3 课堂小结:求一个圆周角的角度时,可求与之相等的另一个圆周角或同弧所对的圆周角度数. 二、课堂展示、体系建构(例题展示,变式操练) 1、能根据圆周角定理转换思维顺利解题 2、熟练掌握圆周角定理 能真正理解掌握圆周角定理的推论 准确熟练地运用推论解题 课堂小结:将课堂小结的核心知识点做好笔记。 课堂中阶段通过变式训练,进一步巩固所学,拓展知识,为当堂测评高过关率作好充分的铺垫。进一步规范解题格式,探索解题思想方法。 归纳所学,建构认知体系。
当堂测评 分享收获 三、监测反馈、辅导调整(精选试题,实施检测) 1、当堂测评:《练习册 》(课后作业)第99页:1、2、3、4、5(每题20分,共100分),附加题:第99页:6(50分) 2、课堂巡视,了解检测情况,个别面辅,收集共性问题在练习课上重点解决。 3、选择性点评共性问题。 三、兴趣信心、互助提升(满意高分,组间争雄) 1、独立作答,仔细检查,余下的考试时间完成当天课后作业题。 2、组间交换批阅(也可收交教师批阅),试题后返还,组长统分,交科代表汇总上报老师。 3、先独立安静纠错,无法解决的问题可轻声请教组内同学“一帮一”。 课堂后阶段通过当堂测评反馈教学效果,及时解决存在问题。多数学生能考出高分数,分享学习数学的愉悦。
课后作业 预习作业:认真阅读教材第87-88页内容,铅笔勾画重点概念,完成《练习册》71页例1、例2; 2、课后作业:《练习册》课后作业(白册子)7、8、9、10、11题。余下各题学有余力学生选做(难题课后个别辅导)。
教学反思
1
上课教师 上课时间 第 周 第 节
教学 目标 1、理解圆周角的定义,会区分圆周角和圆心角。 2、掌握圆周角定理,并会用此定理进行简单的论证和计算。 3、在探索学习过程中增强自主学习独立思考能力,提升学习信心。
教学 重点 圆周角的定理、圆周角的定理的推导及运用它们解题
教学 难点 圆周角的定理、圆周角的定理的推导及运用它们解题
教 学 过 程
环节 教师活动 学生活动 设计意图
课前预习 1、布置学生的课前预习任务 2、进行预习方法指导 3、对学生预习任务的检查与评定。 1、认真阅读教材第85-86页内容,铅笔勾画重点概念 2、完成《新课程实践与探案丛书》(以后简称《练习册》)课堂练习69-70页例1、例2。 培养学生课前预习习惯,提升学生自主学习能力。
自主学习 理解新知 一、师生互动、引问激思(运用教材,梳理知识) 1、圆周角定义及定理 例1:如图,AB是⊙O的直径,C,D是⊙O上的两点,分别连接AC,BC,CD,OD.若∠DOB=140°,则∠ACD=( )(练习册69页例1) A.20° B.30° C.40° D.70° 2、圆周角定理的推论 例2:如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD. 求证:△ABD是等边三角形; 若BD=3,求⊙O的半径.(练习册70页例2) 一、进入情境、领会所学(理解教材,领悟新知) 1、请同学分享例1解答 2、说出圆周角的概念及用自己的语言表述圆周角定理(完成教材第85-86页内容的理解) 3、在书上将相关知识点进行勾画 1、请同学展示例2解答 2、用自己的语言说出圆周角定理的推论 3、解题思路准确,规范解题过程 4、将书上相关内容做好勾画 课堂前阶段通过课堂师生互动,学生初步领会本课核心内容。 从教材阅读对基本概念有初步认识,通过练习加强对基本概念的理解。 相关题型的解答能抓住知识点,正确运用。
互动交流 巩固所学 二、点导评析、归类拓展(运用教辅,解疑释惑) 例1变式:如图,点A,B,C均在⊙O上,当∠OBC=40°时∠A的度数是( )(练习册70页变式训练1) A.50° B.55° C.60° D.65° 例2变式:如图,点C,E在⊙O上,OC⊥AB于点D,∠E=22.5°,AB=4,则半径OB等于( )(练习册70页变式训练2) A. B.2 C.2 D.3 课堂小结:求一个圆周角的角度时,可求与之相等的另一个圆周角或同弧所对的圆周角度数. 二、课堂展示、体系建构(例题展示,变式操练) 1、能根据圆周角定理转换思维顺利解题 2、熟练掌握圆周角定理 能真正理解掌握圆周角定理的推论 准确熟练地运用推论解题 课堂小结:将课堂小结的核心知识点做好笔记。 课堂中阶段通过变式训练,进一步巩固所学,拓展知识,为当堂测评高过关率作好充分的铺垫。进一步规范解题格式,探索解题思想方法。 归纳所学,建构认知体系。
当堂测评 分享收获 三、监测反馈、辅导调整(精选试题,实施检测) 1、当堂测评:《练习册 》(课后作业)第99页:1、2、3、4、5(每题20分,共100分),附加题:第99页:6(50分) 2、课堂巡视,了解检测情况,个别面辅,收集共性问题在练习课上重点解决。 3、选择性点评共性问题。 三、兴趣信心、互助提升(满意高分,组间争雄) 1、独立作答,仔细检查,余下的考试时间完成当天课后作业题。 2、组间交换批阅(也可收交教师批阅),试题后返还,组长统分,交科代表汇总上报老师。 3、先独立安静纠错,无法解决的问题可轻声请教组内同学“一帮一”。 课堂后阶段通过当堂测评反馈教学效果,及时解决存在问题。多数学生能考出高分数,分享学习数学的愉悦。
课后作业 预习作业:认真阅读教材第87-88页内容,铅笔勾画重点概念,完成《练习册》71页例1、例2; 2、课后作业:《练习册》课后作业(白册子)7、8、9、10、11题。余下各题学有余力学生选做(难题课后个别辅导)。
教学反思
1
同课章节目录
