2014-2015湘教版数学七年级下册3.2《提公因式法》课件1(共18张PPT)
文档属性
| 名称 | 2014-2015湘教版数学七年级下册3.2《提公因式法》课件1(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 754.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-03 20:17:04 | ||
图片预览






文档简介
课件18张PPT。提公因式法(一)请把12、15因数分解:12=2×2×3;
15=3×512、15这两数有公因数吗?说一说下列每个式子含字母的因式有哪些?
xy, xz, xw由此看出,xy,xz,xw有公共的因式x几个多项式的公共的因式称为它们的公因式。如何把多项式xy+xz+xw 因式分解?合作探究应提取的公因式为:________议一议:多项式 有公因式吗?是什么?
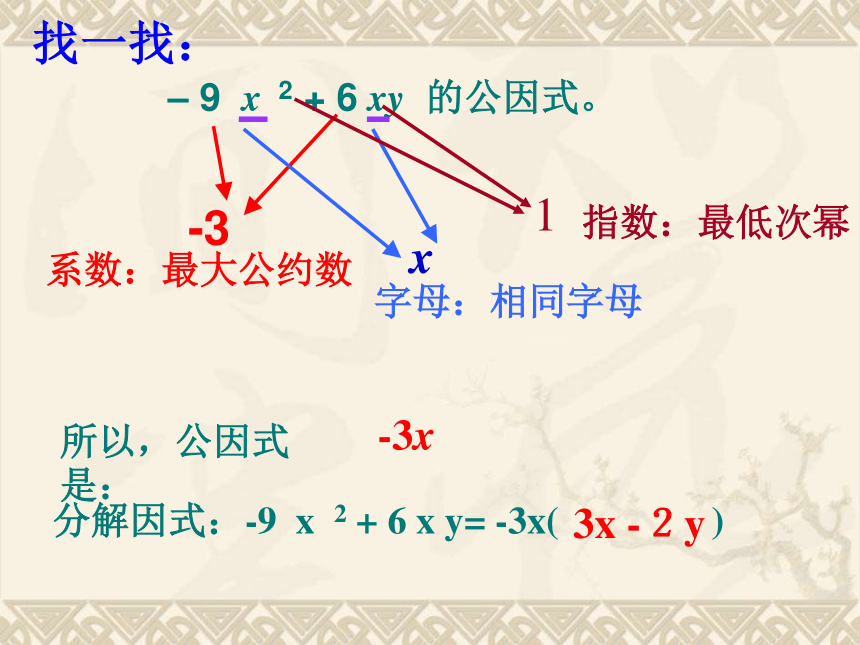
– 9 x 2 + 6 xy 的公因式。系数:最大公约数-3字母:相同字母x 所以,公因式是:指数:最低次幂1-3x分解因式:-9 x 2 + 6 x y= -3x( )3x -2y找一找:2.字母(或式子):1.系数:找公因式的方法:1. 3x2-6y _______
2. 2a+3ab _______3 a3.-30mb2+5nb3 ;-5b2 4.多项式3a(b-c)+8(b-c)2的公因式是 ;(b-c)5.多项式15a2b3 - 6a3bc的公因式是 ;3a2b提取各项系数的绝对值的最大公约数,如果多项式的首项是负数,那么公因式的符号取“_”,但要注意括号内各项的符号都要改变!提取各项相同的字母(或式子);3.指数:提取各项所含相同字母(或式子)的最低次幂解 括号内的第3项为1 由于x = x · 1,因此第三项将x提出后,括号内的因式为“1”.分析:多项式各项均含有x,因此公因式为x。 第3项将x提出后,括号内的因式 是多少?注意:
当公因式与多项式中的某一项相同或相反时,提取公因式之后,括号里面应该用“1”或者“-1”来代替把 因式分解.2、公因式的字母取各项都含有的字母“x”.3、“x”的指数取各项中
次数最低的1次。1、系数取各项系数的绝对值4,6的最大公因数2 第1项的系数为负,最好把负号提出,使括号内的第1项的系数为正.分析:先确定公因式的系数,再确定字母,最后确定字母的指数。因此公因式为“-2x”. 由此看出,-2x是这个多项式各项的公因式,把-2x提出后,括号内各项的系数如何计算?解 注意同号两数相除得正数,异号两数相除得负数,因此把负号提出后,括号内的各项要变号. 用公因式的系数-2去除原来多项式的各项系数,所得的商就是括号内的各项系数.把 因式分解.公因式中含有哪些字母?它们的指数取多少? 4xy2 是公因式,把 4xy2 提出后,括号
内的各项是什么样子?公因式含的字母是各项中相同的字母x,y,它们的指数应当取它们在各项中次数最低的.分析 公因式的系数如何确定?是8与12的最大公因数4解由于第1项可以写成
因此括号内的第1项为 2xy2由于第2项可以写成
因此括号内的第2项为 -3z提取公因式法的一般步骤:
1.确定应提取的公因式;2.用公因式去除这个多项式,所得的商作为另一个因式3.把多项式写成这两个因式的积的形式。①提取不尽③疏忽变号④只提取部分公因式,整个式子未写成乘积形式。(2)提取公因式要彻底;注意易犯的错误:②漏项(1)当首项系数为负数时,通常应提取负号,在提取“-”号时,余下括号内的各项都变号。重点注意:(3)可以运用整式乘法进行检验。归纳总结1.说出下列多项式中各项的公因式:公因式:-3y考考你公因式:公因式:2xm-1yn-13.把下列多项式因式分解:(1)2x2 + 3x3 + x = x(2x +3x2)(2)a2c - 6a3c = a2(c - 6ac)(3)-2s3 + 4s2 - 6s = - s(2s2 + 4s - 6)(4)a2b + 6ab2 - 8a = -2ab(2a-3b) - 8a4.下列的分解因式对吗?如不对,请指出原因:漏项: 原式=x(2x +3x2+1)分解不彻底与符号错误: 原式=-2s(s2-2s+3)结果不是乘积形式: 原式= a(ab+6b2-8)分解不彻底: 原式=a2c(1 -6a)1、确定公因式的方法:
(1)公因式的系数取各项系数的绝对值的最大公因数。
(2)公因式的字母(或式子)取各项中都含有的相同的字母(或式子) 。
(3)公因式中相同字母(或式子)的指数取各项中指数最低的,即最低次幂。小结2、提取公因式法的步骤:(1)确定应提取的公因式;(2)用公因式去除这个多项式,所得的商作为另一个因式(3)把多项式写成这两个因式的积的形式。注意:提取公因式时,有时需要将因式经过符号变换、字母位置重新排列或添括号后,才能看出公因式。= (a-b)(2a-2b-1)= (a-b)[2(a-b)-1]= 2(a-b)2-(a-b)2(a-b)2 – a + b解:拓展练习:把2(a-b)2 - a + b 分解因式
15=3×512、15这两数有公因数吗?说一说下列每个式子含字母的因式有哪些?
xy, xz, xw由此看出,xy,xz,xw有公共的因式x几个多项式的公共的因式称为它们的公因式。如何把多项式xy+xz+xw 因式分解?合作探究应提取的公因式为:________议一议:多项式 有公因式吗?是什么?
– 9 x 2 + 6 xy 的公因式。系数:最大公约数-3字母:相同字母x 所以,公因式是:指数:最低次幂1-3x分解因式:-9 x 2 + 6 x y= -3x( )3x -2y找一找:2.字母(或式子):1.系数:找公因式的方法:1. 3x2-6y _______
2. 2a+3ab _______3 a3.-30mb2+5nb3 ;-5b2 4.多项式3a(b-c)+8(b-c)2的公因式是 ;(b-c)5.多项式15a2b3 - 6a3bc的公因式是 ;3a2b提取各项系数的绝对值的最大公约数,如果多项式的首项是负数,那么公因式的符号取“_”,但要注意括号内各项的符号都要改变!提取各项相同的字母(或式子);3.指数:提取各项所含相同字母(或式子)的最低次幂解 括号内的第3项为1 由于x = x · 1,因此第三项将x提出后,括号内的因式为“1”.分析:多项式各项均含有x,因此公因式为x。 第3项将x提出后,括号内的因式 是多少?注意:
当公因式与多项式中的某一项相同或相反时,提取公因式之后,括号里面应该用“1”或者“-1”来代替把 因式分解.2、公因式的字母取各项都含有的字母“x”.3、“x”的指数取各项中
次数最低的1次。1、系数取各项系数的绝对值4,6的最大公因数2 第1项的系数为负,最好把负号提出,使括号内的第1项的系数为正.分析:先确定公因式的系数,再确定字母,最后确定字母的指数。因此公因式为“-2x”. 由此看出,-2x是这个多项式各项的公因式,把-2x提出后,括号内各项的系数如何计算?解 注意同号两数相除得正数,异号两数相除得负数,因此把负号提出后,括号内的各项要变号. 用公因式的系数-2去除原来多项式的各项系数,所得的商就是括号内的各项系数.把 因式分解.公因式中含有哪些字母?它们的指数取多少? 4xy2 是公因式,把 4xy2 提出后,括号
内的各项是什么样子?公因式含的字母是各项中相同的字母x,y,它们的指数应当取它们在各项中次数最低的.分析 公因式的系数如何确定?是8与12的最大公因数4解由于第1项可以写成
因此括号内的第1项为 2xy2由于第2项可以写成
因此括号内的第2项为 -3z提取公因式法的一般步骤:
1.确定应提取的公因式;2.用公因式去除这个多项式,所得的商作为另一个因式3.把多项式写成这两个因式的积的形式。①提取不尽③疏忽变号④只提取部分公因式,整个式子未写成乘积形式。(2)提取公因式要彻底;注意易犯的错误:②漏项(1)当首项系数为负数时,通常应提取负号,在提取“-”号时,余下括号内的各项都变号。重点注意:(3)可以运用整式乘法进行检验。归纳总结1.说出下列多项式中各项的公因式:公因式:-3y考考你公因式:公因式:2xm-1yn-13.把下列多项式因式分解:(1)2x2 + 3x3 + x = x(2x +3x2)(2)a2c - 6a3c = a2(c - 6ac)(3)-2s3 + 4s2 - 6s = - s(2s2 + 4s - 6)(4)a2b + 6ab2 - 8a = -2ab(2a-3b) - 8a4.下列的分解因式对吗?如不对,请指出原因:漏项: 原式=x(2x +3x2+1)分解不彻底与符号错误: 原式=-2s(s2-2s+3)结果不是乘积形式: 原式= a(ab+6b2-8)分解不彻底: 原式=a2c(1 -6a)1、确定公因式的方法:
(1)公因式的系数取各项系数的绝对值的最大公因数。
(2)公因式的字母(或式子)取各项中都含有的相同的字母(或式子) 。
(3)公因式中相同字母(或式子)的指数取各项中指数最低的,即最低次幂。小结2、提取公因式法的步骤:(1)确定应提取的公因式;(2)用公因式去除这个多项式,所得的商作为另一个因式(3)把多项式写成这两个因式的积的形式。注意:提取公因式时,有时需要将因式经过符号变换、字母位置重新排列或添括号后,才能看出公因式。= (a-b)(2a-2b-1)= (a-b)[2(a-b)-1]= 2(a-b)2-(a-b)2(a-b)2 – a + b解:拓展练习:把2(a-b)2 - a + b 分解因式
