勾股定理一(湖北省襄樊市保康县)
文档属性
| 名称 | 勾股定理一(湖北省襄樊市保康县) |  | |
| 格式 | rar | ||
| 文件大小 | 431.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-11 15:42:00 | ||
图片预览


文档简介
课件14张PPT。勾股定理欢迎你
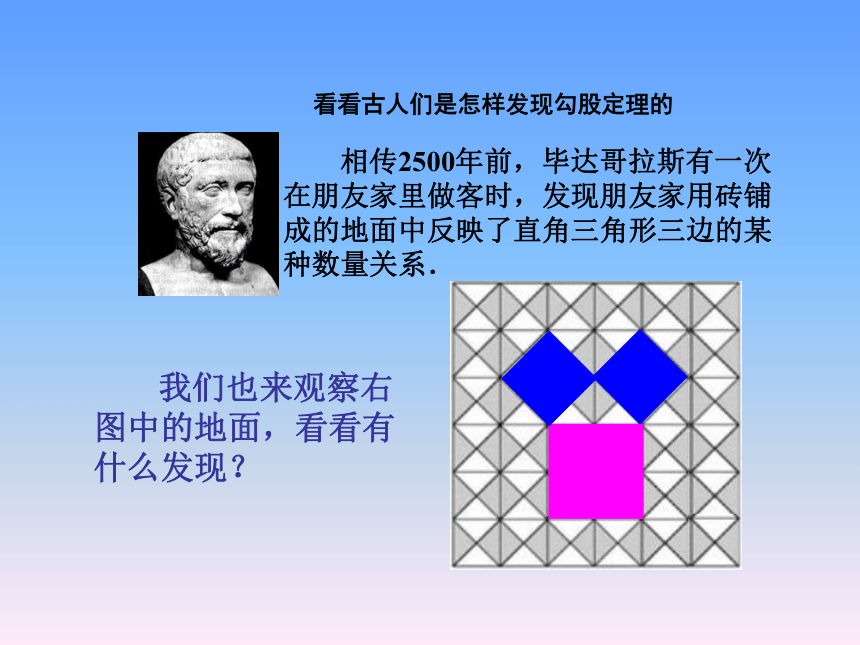
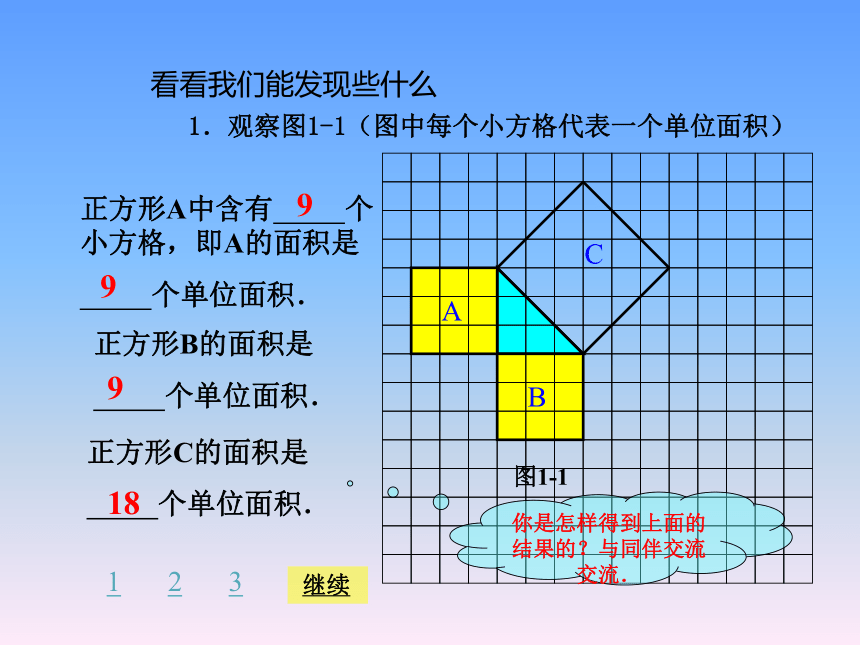
-----八一班的全体同学们这就是本届大会会徽的图案.是什么勾起了我们的回忆你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.看看古人们是怎样发现勾股定理的 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?1.观察图1-1(图中每个小方格代表一个单位面积)正方形A中含有 个小方格,即A的面积是
个单位面积.正方形B的面积是
个单位面积.正方形C的面积是
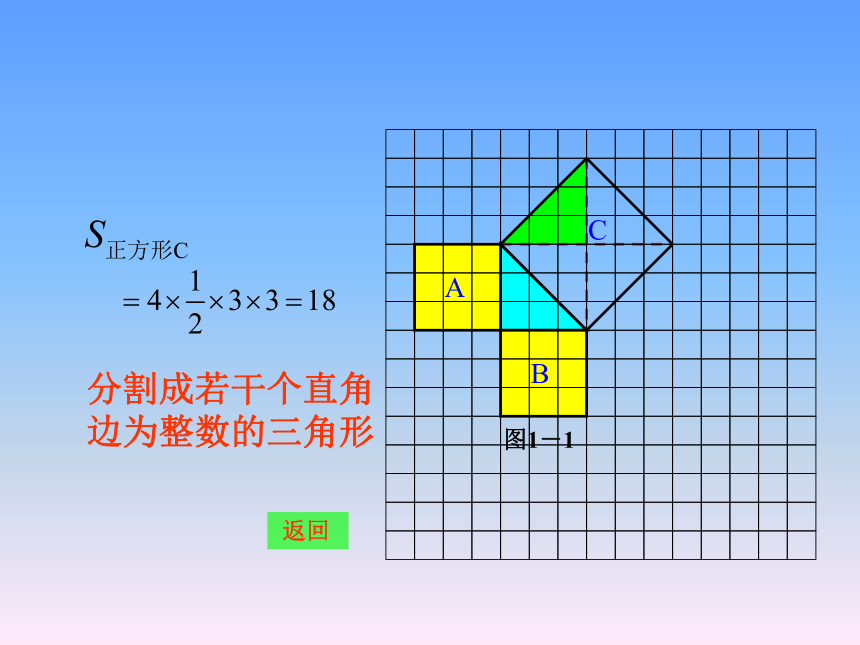
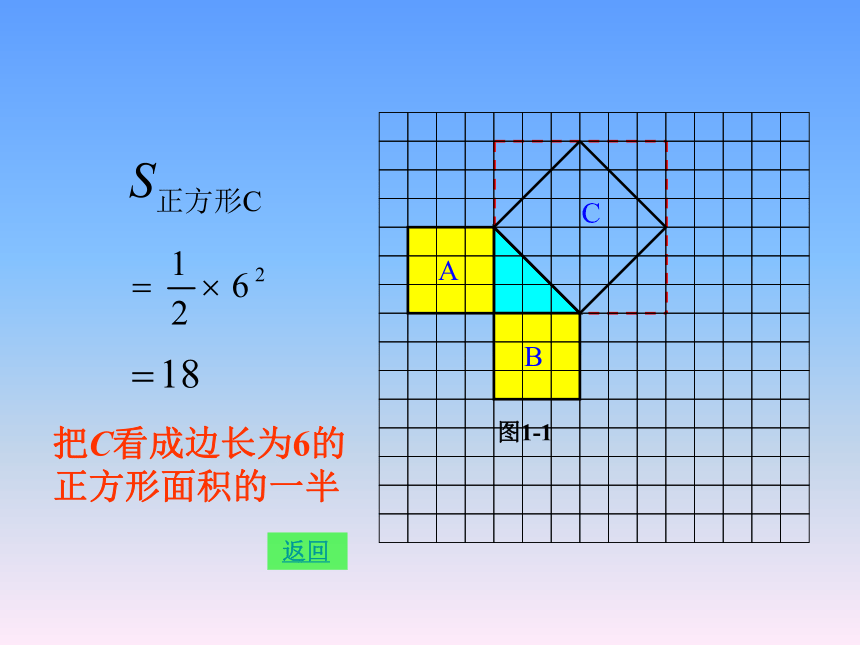
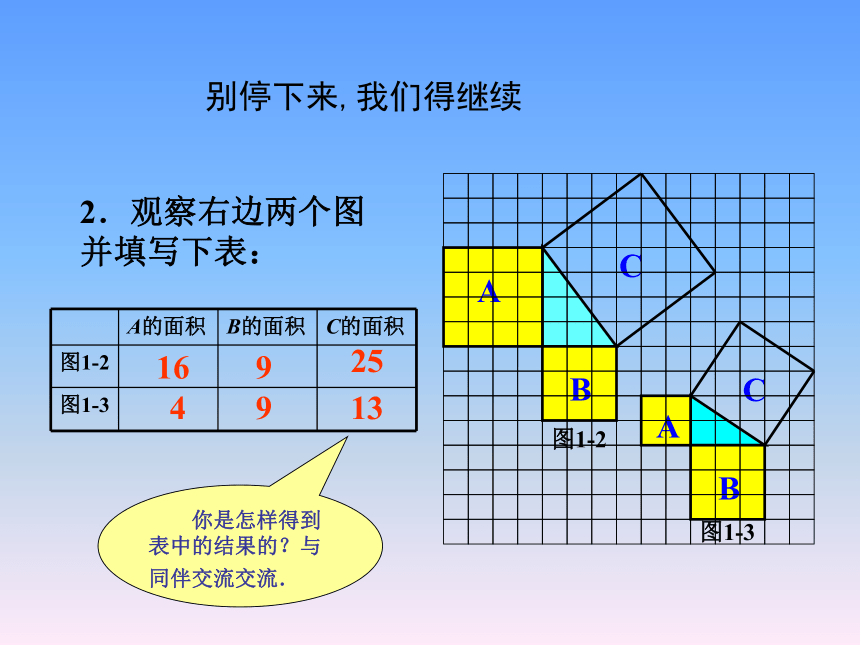
个单位面积.9918你是怎样得到上面的结果的?与同伴交流交流.1239 继续看看我们能发现些什么图1-1分割成若干个直角边为整数的三角形 返回把C看成边长为6的正方形面积的一半 返回2.观察右边两个图并填写下表:169254913 你是怎样得到表中的结果的?与同伴交流交流.别停下来,我们得继续3.三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.该是发现的时候了4.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.5.分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.第4 题中的关系对这个三角形仍然成立吗?直角三角形两直角边的平方和等于斜边的平方. 是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面我们就来看一看我国数学家赵爽是怎样证明这个命题的.我们绝逊于古人了吗看看古人是如何证明勾股定理的 看左边的图案,这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
赵爽弦图的证法化简得: c2 =a2+ b2. 勾股定理 如果直角三角形两直角边分别为a、b,斜边为c,那么 直角三角形两直角边的平方和等于斜边的平方.说说本节课的收获作业: 勾股定理从边的角度刻画了直角三角形的又一个特征.
人类对勾股定理的研究已有近3000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥定理”等等 . 收集有关勾股定理的证明方法,下节课展示、交流.
-----八一班的全体同学们这就是本届大会会徽的图案.是什么勾起了我们的回忆你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.看看古人们是怎样发现勾股定理的 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?1.观察图1-1(图中每个小方格代表一个单位面积)正方形A中含有 个小方格,即A的面积是
个单位面积.正方形B的面积是
个单位面积.正方形C的面积是
个单位面积.9918你是怎样得到上面的结果的?与同伴交流交流.1239 继续看看我们能发现些什么图1-1分割成若干个直角边为整数的三角形 返回把C看成边长为6的正方形面积的一半 返回2.观察右边两个图并填写下表:169254913 你是怎样得到表中的结果的?与同伴交流交流.别停下来,我们得继续3.三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.该是发现的时候了4.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.5.分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.第4 题中的关系对这个三角形仍然成立吗?直角三角形两直角边的平方和等于斜边的平方. 是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面我们就来看一看我国数学家赵爽是怎样证明这个命题的.我们绝逊于古人了吗看看古人是如何证明勾股定理的 看左边的图案,这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
赵爽弦图的证法化简得: c2 =a2+ b2. 勾股定理 如果直角三角形两直角边分别为a、b,斜边为c,那么 直角三角形两直角边的平方和等于斜边的平方.说说本节课的收获作业: 勾股定理从边的角度刻画了直角三角形的又一个特征.
人类对勾股定理的研究已有近3000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥定理”等等 . 收集有关勾股定理的证明方法,下节课展示、交流.
