平行四边形性质课件(湖北省武汉市)
文档属性
| 名称 | 平行四边形性质课件(湖北省武汉市) |  | |
| 格式 | rar | ||
| 文件大小 | 429.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-11 15:46:00 | ||
图片预览



文档简介
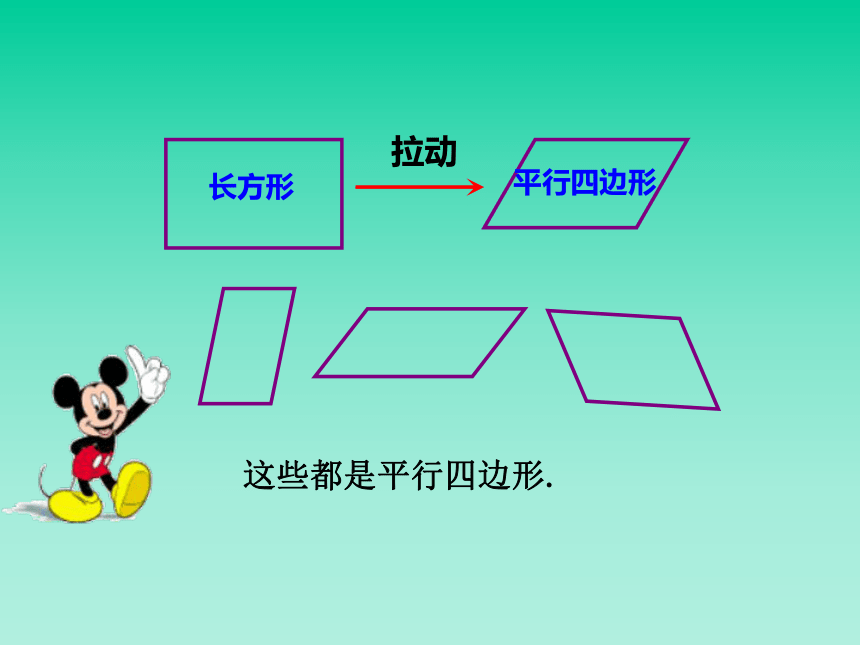
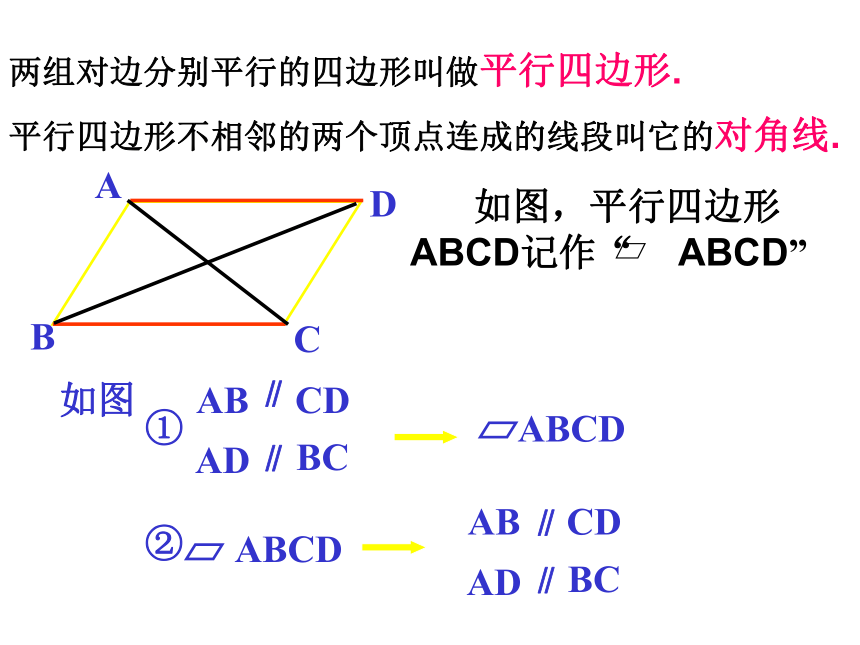
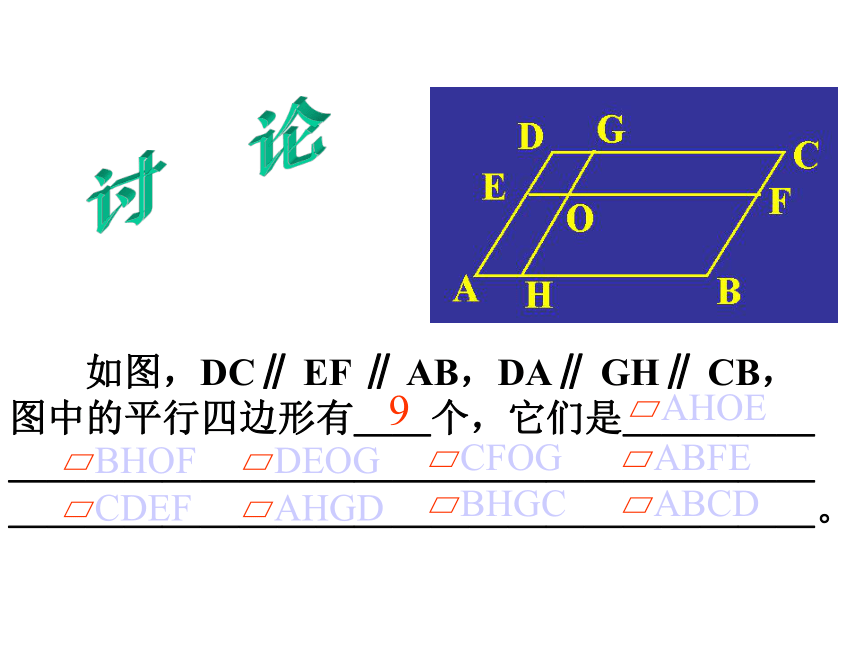
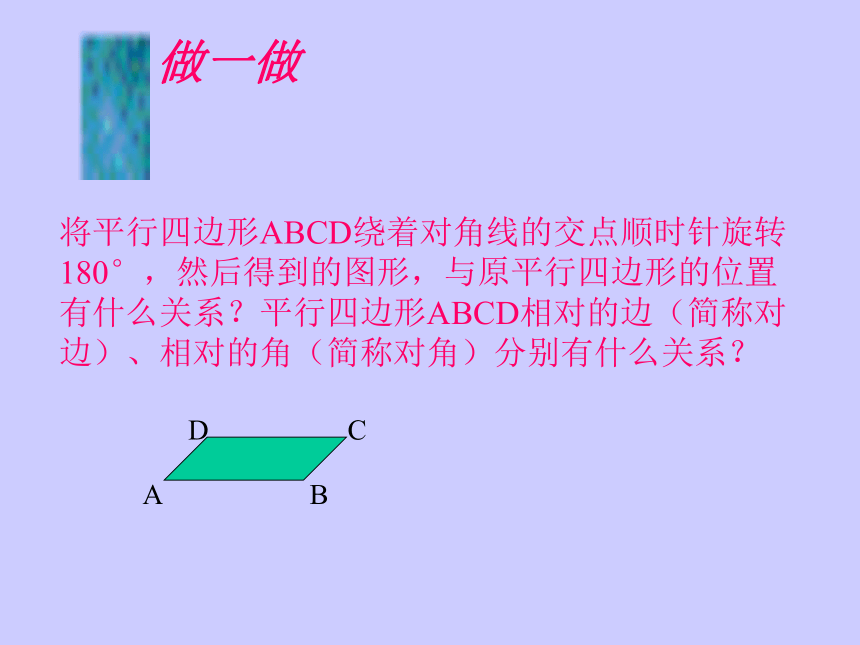
课件25张PPT。平行四边形的性质拉动长方形平行四边形这些都是平行四边形.两组对边分别平行的四边形叫做平行四边形.平行四边形不相邻的两个顶点连成的线段叫它的对角线.∥∥∥∥ 如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。讨 论9做一做
平行四边形:
两组对边分别相等
两组对角分别相等 验证探索自我评价标准
合格:每个结论用了一种方法验证
良好:每个结论用了两种方法验证
优秀:每个结论用了三种或者三种以上的方法
验证 探索用什么方法验证推理∠1= ∠2∠3= ∠4∠BAD= ∠BCD∥∥?CDA?ABC看我的平行四边形的性质:性质1:平行四边形的对角相等。几何语言:∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D。性质2:平行四边形的对边相等。几何语言:∵四边形ABCD是平行四边形∴AB=CD,BC=AD。
选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数为
( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm 练一练C A 解:∵四边形ABCD是平行四边形且∠A=32°(已知)∴ ∠A=∠C=32°,∠B=∠D(平行四边形的 对角相等)又∵AD∥BC(平行四边形的对边平行)∴∠A+∠B=180°(两直线平行,同旁内角互补)∴∠B=∠D= 180 °-∠A= 180o-32°=148 °平行四边形中有一隐含条件:平行四边形邻角互补。32°M1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点P、Q,求证:MQ=NPADBNQCP证明:∵四边形ABCD是平行四边形
∴AD∥BC,AB ∥ CD
即AM ∥ CQ.
又AC ∥ MN,即AC ∥ MQ
∴四边形MQCA是平行四边形
∴ MQ=AC
同理可证:NP=AC
∴MQ=NP 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:平行四边形可以看作是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。试一试如图,已知平行四边形ABCD,以一组对边AD、BC向形外作等边△ADE和等边△ BCF,连结BE、DF,探索BE、DF的大小关系。
平行且相等相等互补∠A=∠C, ∠B=∠D∠A+∠B=180°你学会了吗?小结1.平行四边形的概念
2.平行四边形的性质
3.解决平行四边形的有关问题经常连结
对角线转化为三角形。欣赏七巧板拼图来看我的再见!谢谢!
平行四边形:
两组对边分别相等
两组对角分别相等 验证探索自我评价标准
合格:每个结论用了一种方法验证
良好:每个结论用了两种方法验证
优秀:每个结论用了三种或者三种以上的方法
验证 探索用什么方法验证推理∠1= ∠2∠3= ∠4∠BAD= ∠BCD∥∥?CDA?ABC看我的平行四边形的性质:性质1:平行四边形的对角相等。几何语言:∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D。性质2:平行四边形的对边相等。几何语言:∵四边形ABCD是平行四边形∴AB=CD,BC=AD。
选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数为
( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm 练一练C A 解:∵四边形ABCD是平行四边形且∠A=32°(已知)∴ ∠A=∠C=32°,∠B=∠D(平行四边形的 对角相等)又∵AD∥BC(平行四边形的对边平行)∴∠A+∠B=180°(两直线平行,同旁内角互补)∴∠B=∠D= 180 °-∠A= 180o-32°=148 °平行四边形中有一隐含条件:平行四边形邻角互补。32°M1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点P、Q,求证:MQ=NPADBNQCP证明:∵四边形ABCD是平行四边形
∴AD∥BC,AB ∥ CD
即AM ∥ CQ.
又AC ∥ MN,即AC ∥ MQ
∴四边形MQCA是平行四边形
∴ MQ=AC
同理可证:NP=AC
∴MQ=NP 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:平行四边形可以看作是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。试一试如图,已知平行四边形ABCD,以一组对边AD、BC向形外作等边△ADE和等边△ BCF,连结BE、DF,探索BE、DF的大小关系。
平行且相等相等互补∠A=∠C, ∠B=∠D∠A+∠B=180°你学会了吗?小结1.平行四边形的概念
2.平行四边形的性质
3.解决平行四边形的有关问题经常连结
对角线转化为三角形。欣赏七巧板拼图来看我的再见!谢谢!
