17.1勾股定理同步训练(无答案)2022-—2023学年人教版数学八年级下册
文档属性
| 名称 | 17.1勾股定理同步训练(无答案)2022-—2023学年人教版数学八年级下册 | 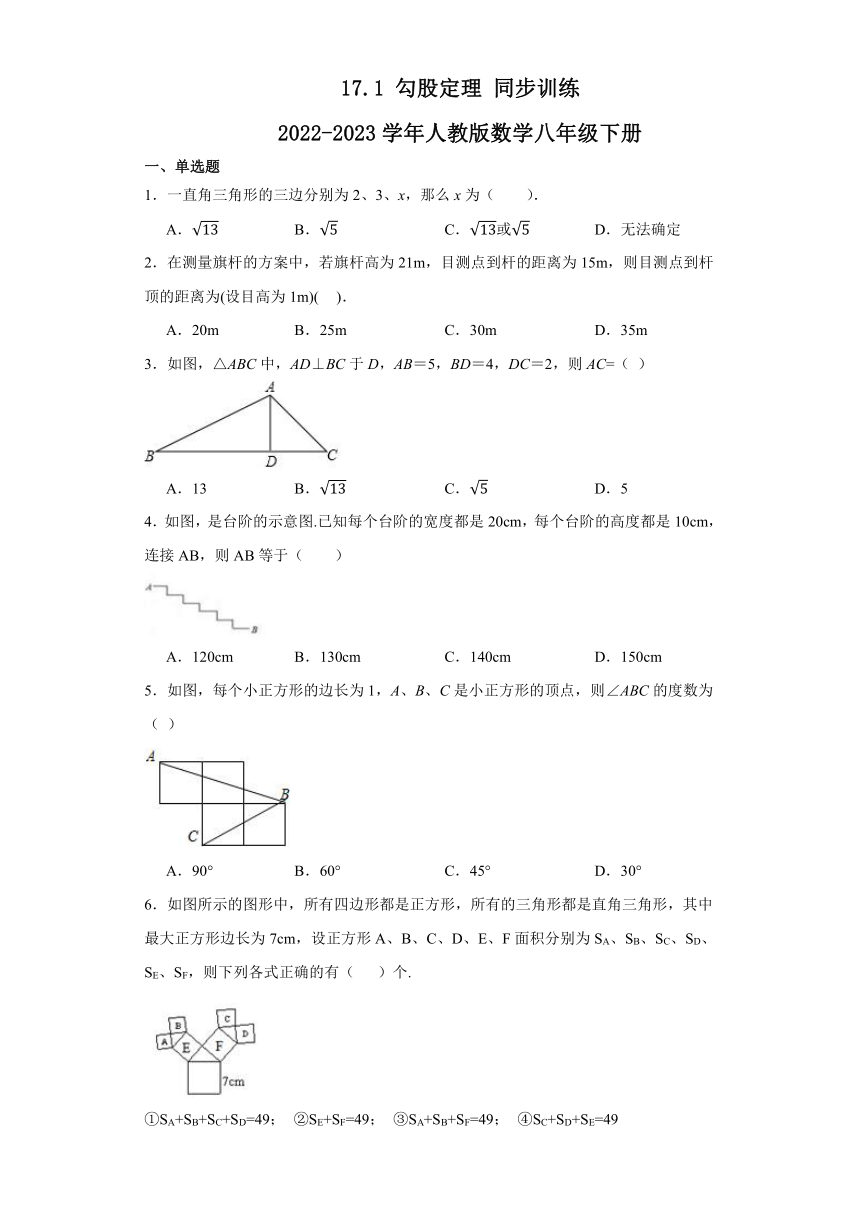 | |
| 格式 | docx | ||
| 文件大小 | 414.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 20:36:31 | ||
图片预览

文档简介
17.1 勾股定理 同步训练
2022-2023学年人教版数学八年级下册
一、单选题
1.一直角三角形的三边分别为2、3、x,那么x为( ).
A. B. C.或 D.无法确定
2.在测量旗杆的方案中,若旗杆高为21m,目测点到杆的距离为15m,则目测点到杆顶的距离为(设目高为1m)( ).
A.20m B.25m C.30m D.35m
3.如图,△ABC中,AD⊥BC于D,AB=5,BD=4,DC=2,则AC=( )
A.13 B. C. D.5
4.如图,是台阶的示意图.已知每个台阶的宽度都是20cm,每个台阶的高度都是10cm,连接AB,则AB等于( )
A.120cm B.130cm C.140cm D.150cm
5.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
6.如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确的有( )个.
①SA+SB+SC+SD=49; ②SE+SF=49; ③SA+SB+SF=49; ④SC+SD+SE=49
A.1 B.2 C.3 D.4
7.如图,圆柱底面半径为cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.12cm B.cm C.15cm D.cm
8.下图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.黄金分割 B.垂径定理 C.勾股定理 D.正弦定理
二、填空题
9.已知等腰三角形的一边长为10,面积为30,该三角形的周长为 .
10.在△ABC中,∠B=90度,BC=6,AC=8,则AB= .
11.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 尺.
12.如图所示,在数轴上点A所表示的数为a,则a的值为 .
13.如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为 .
14.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为 m.
三、解答题
15.如图,已知AD是△ABC的高,∠BAC=60°,BD=2CD=2,试求AB的长.
16.如图,圆柱形玻璃杯的高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为多少
17.如图,在中,,,AD是的角平分线,,垂足为E.
求证:;
已知,求AC的长;
求证:.
18.一架梯子长13米,斜靠在一面墙上,梯子底端离墙5米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了7米到C,那么梯子的底端在水平方向滑动了几米?
2022-2023学年人教版数学八年级下册
一、单选题
1.一直角三角形的三边分别为2、3、x,那么x为( ).
A. B. C.或 D.无法确定
2.在测量旗杆的方案中,若旗杆高为21m,目测点到杆的距离为15m,则目测点到杆顶的距离为(设目高为1m)( ).
A.20m B.25m C.30m D.35m
3.如图,△ABC中,AD⊥BC于D,AB=5,BD=4,DC=2,则AC=( )
A.13 B. C. D.5
4.如图,是台阶的示意图.已知每个台阶的宽度都是20cm,每个台阶的高度都是10cm,连接AB,则AB等于( )
A.120cm B.130cm C.140cm D.150cm
5.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
6.如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确的有( )个.
①SA+SB+SC+SD=49; ②SE+SF=49; ③SA+SB+SF=49; ④SC+SD+SE=49
A.1 B.2 C.3 D.4
7.如图,圆柱底面半径为cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.12cm B.cm C.15cm D.cm
8.下图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.黄金分割 B.垂径定理 C.勾股定理 D.正弦定理
二、填空题
9.已知等腰三角形的一边长为10,面积为30,该三角形的周长为 .
10.在△ABC中,∠B=90度,BC=6,AC=8,则AB= .
11.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 尺.
12.如图所示,在数轴上点A所表示的数为a,则a的值为 .
13.如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为 .
14.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为 m.
三、解答题
15.如图,已知AD是△ABC的高,∠BAC=60°,BD=2CD=2,试求AB的长.
16.如图,圆柱形玻璃杯的高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为多少
17.如图,在中,,,AD是的角平分线,,垂足为E.
求证:;
已知,求AC的长;
求证:.
18.一架梯子长13米,斜靠在一面墙上,梯子底端离墙5米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了7米到C,那么梯子的底端在水平方向滑动了几米?
