24.1.4圆周角 同步练习(无答案)2023-2024学年人教版 数学 九年级 上册
文档属性
| 名称 | 24.1.4圆周角 同步练习(无答案)2023-2024学年人教版 数学 九年级 上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 337.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 20:37:13 | ||
图片预览




文档简介
24.1.4圆周角
一、选择题。
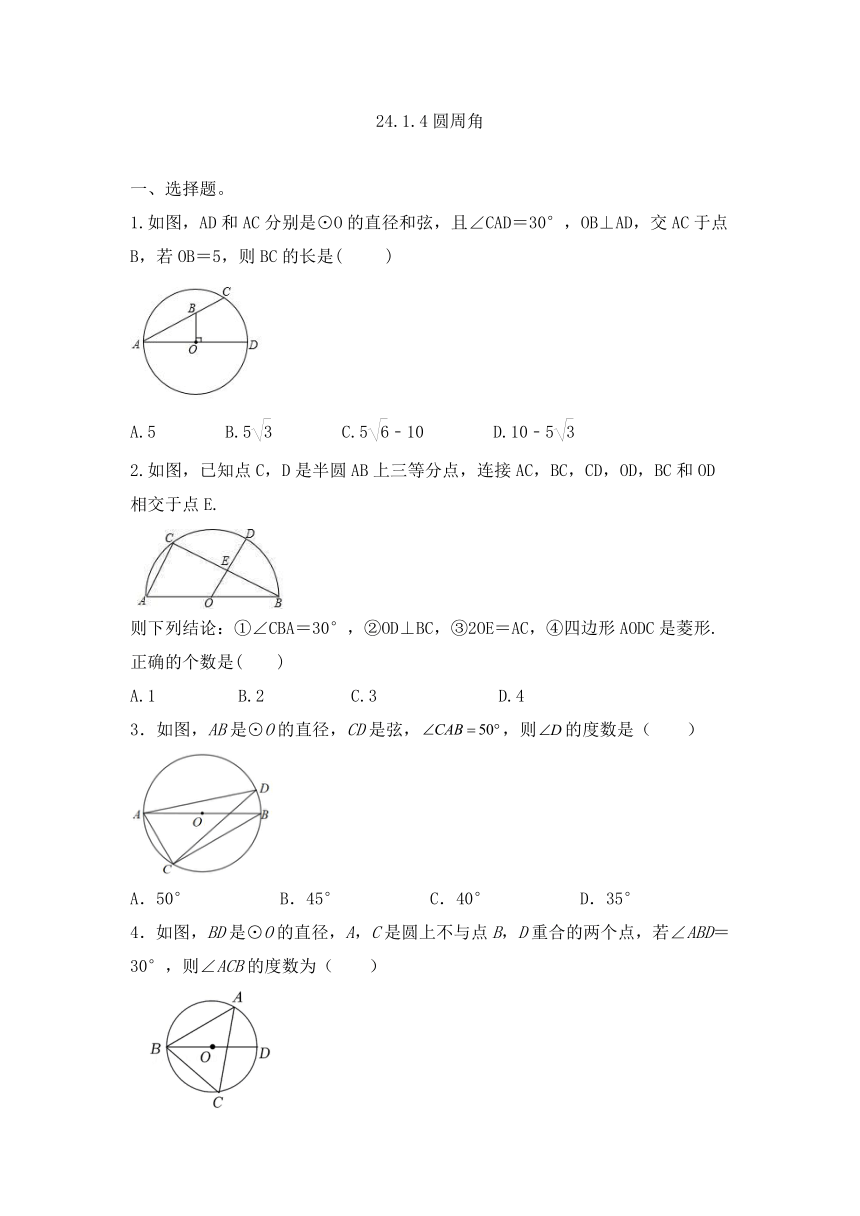
1.如图,AD和AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=5,则BC的长是( )
A.5 B.5 C.5﹣10 D.10﹣5
2.如图,已知点C,D是半圆AB上三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.
则下列结论:①∠CBA=30°,②OD⊥BC,③2OE=AC,④四边形AODC是菱形.
正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,AB是⊙O的直径,CD是弦,,则的度数是( )
A.50° B.45° C.40° D.35°
4.如图,BD是⊙O的直径,A,C是圆上不与点B,D重合的两个点,若∠ABD=30°,则∠ACB的度数为( )
A.30° B.45° C.60° D.75°
5.如图,O的直径AB=8,∠A=30°,点P在线段AB上,则PC的最小值为( )
A.2 B. C.4 D.
6.如图,在直径为AB的⊙O中,点C,D在圆上,AC=CD,若∠CAD=28°,则∠DAB的度数为( )
A.28° B.34° C.56° D.62°
7.如图,已知AB是半⊙O的直径,点C,D都在上,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论错误的是( )
A.AD⊥BD B.AF=DF C.∠AOC=∠AEC D.BD=2OF
8.如图,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴正半轴上,且∠ACB=45°,则点C的坐标为( )
A.(0,7) B.(0,2) C.(0,6) D.(0,3)
9.如图,菱形ABCO的顶点O为⊙O的圆心,顶点A,B,C均在圆周上,则∠A的度数是( )
A.30° B.45° C.60° D.75°
10.如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设的度数为28°,则∠CBD的度数为( )
A.14° B.28° C.31° D.62°
11.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为10,则弦AB长为( )
A.10 B.5 C. D.
12.如图,是的弦,交于点,点是上一点,,则的度数为( )
A. B. C. D.
13.如图,△ABC的顶点A、B、C均在⊙O上,连接OA,OC,若∠ABC+∠AOC
=75°,则∠OAC的度数是( )
A.45° B.50° C.60° D.65°
14.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+AC2=4;
②∠DBC+∠ADO=90°;
③若AC=BD,则DE=OE;
④若点P为BD的中点,则DE=2OE.其中正确的是( )
A.①②③ B.②③④ C.③④ D.②④
二、填空题。
1.如图,圆O的直径AB为13cm,弦AC为5cm,∠ACB的平分线圆O于D,则CD长是______cm.
2.如图,AB是☉O的直径,CD是☉O的弦,∠CAB=55°,则∠D的度数是 .
3.如图,点A,B,C在⊙O上,若∠ABC=60°,则∠AOC的度数为 .
4.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于 .
5.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,若⊙O的直径为8,则弦AB的长为 .
6.如图,把直角三角板的直角顶点C放在圆周上,两直角边与圆弧分别交于点A,B,量得CB=8cm,CA=6cm,则该圆的半径是 cm.
三、解答题。
1.如图,为的直径,弦,的延长线相交于点,且,求证:.
2.如图,⊙O的半径为2,四边形ABCD内接于⊙O,圆心O到AC的距离等于.
(1)求AC的长;
(2)求∠ADC的度数.
3.如图,四边形ABDC内接于⊙O,∠BOC=120°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=2,求弦AC长.
4.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r.
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
5.如图,AB为⊙O的直径,弦CD⊥AB于点E,连接DO并延长交⊙O于点F,连接AF,∠AFD=∠CDF.
(1)求证:=;
(2)连接AC,若AB=12,求AC的长.
6.如图,在扇形AOB中,∠AOB=90°,C、D是上两点,过点D作DE∥OC交OB于E点,在OD上取点F,使OF=DE,连接CF并延长交OB于G点.
(1)求证:△OCF≌△DOE;
(2)若C、D是的三等分点,:
①求∠OGC;
②请比较GE和BE的大小.
一、选择题。
1.如图,AD和AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=5,则BC的长是( )
A.5 B.5 C.5﹣10 D.10﹣5
2.如图,已知点C,D是半圆AB上三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.
则下列结论:①∠CBA=30°,②OD⊥BC,③2OE=AC,④四边形AODC是菱形.
正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,AB是⊙O的直径,CD是弦,,则的度数是( )
A.50° B.45° C.40° D.35°
4.如图,BD是⊙O的直径,A,C是圆上不与点B,D重合的两个点,若∠ABD=30°,则∠ACB的度数为( )
A.30° B.45° C.60° D.75°
5.如图,O的直径AB=8,∠A=30°,点P在线段AB上,则PC的最小值为( )
A.2 B. C.4 D.
6.如图,在直径为AB的⊙O中,点C,D在圆上,AC=CD,若∠CAD=28°,则∠DAB的度数为( )
A.28° B.34° C.56° D.62°
7.如图,已知AB是半⊙O的直径,点C,D都在上,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论错误的是( )
A.AD⊥BD B.AF=DF C.∠AOC=∠AEC D.BD=2OF
8.如图,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴正半轴上,且∠ACB=45°,则点C的坐标为( )
A.(0,7) B.(0,2) C.(0,6) D.(0,3)
9.如图,菱形ABCO的顶点O为⊙O的圆心,顶点A,B,C均在圆周上,则∠A的度数是( )
A.30° B.45° C.60° D.75°
10.如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设的度数为28°,则∠CBD的度数为( )
A.14° B.28° C.31° D.62°
11.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为10,则弦AB长为( )
A.10 B.5 C. D.
12.如图,是的弦,交于点,点是上一点,,则的度数为( )
A. B. C. D.
13.如图,△ABC的顶点A、B、C均在⊙O上,连接OA,OC,若∠ABC+∠AOC
=75°,则∠OAC的度数是( )
A.45° B.50° C.60° D.65°
14.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+AC2=4;
②∠DBC+∠ADO=90°;
③若AC=BD,则DE=OE;
④若点P为BD的中点,则DE=2OE.其中正确的是( )
A.①②③ B.②③④ C.③④ D.②④
二、填空题。
1.如图,圆O的直径AB为13cm,弦AC为5cm,∠ACB的平分线圆O于D,则CD长是______cm.
2.如图,AB是☉O的直径,CD是☉O的弦,∠CAB=55°,则∠D的度数是 .
3.如图,点A,B,C在⊙O上,若∠ABC=60°,则∠AOC的度数为 .
4.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于 .
5.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,若⊙O的直径为8,则弦AB的长为 .
6.如图,把直角三角板的直角顶点C放在圆周上,两直角边与圆弧分别交于点A,B,量得CB=8cm,CA=6cm,则该圆的半径是 cm.
三、解答题。
1.如图,为的直径,弦,的延长线相交于点,且,求证:.
2.如图,⊙O的半径为2,四边形ABCD内接于⊙O,圆心O到AC的距离等于.
(1)求AC的长;
(2)求∠ADC的度数.
3.如图,四边形ABDC内接于⊙O,∠BOC=120°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=2,求弦AC长.
4.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r.
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
5.如图,AB为⊙O的直径,弦CD⊥AB于点E,连接DO并延长交⊙O于点F,连接AF,∠AFD=∠CDF.
(1)求证:=;
(2)连接AC,若AB=12,求AC的长.
6.如图,在扇形AOB中,∠AOB=90°,C、D是上两点,过点D作DE∥OC交OB于E点,在OD上取点F,使OF=DE,连接CF并延长交OB于G点.
(1)求证:△OCF≌△DOE;
(2)若C、D是的三等分点,:
①求∠OGC;
②请比较GE和BE的大小.
同课章节目录
