24.4 弧长和扇形面积(2课时)教案
文档属性
| 名称 | 24.4 弧长和扇形面积(2课时)教案 | 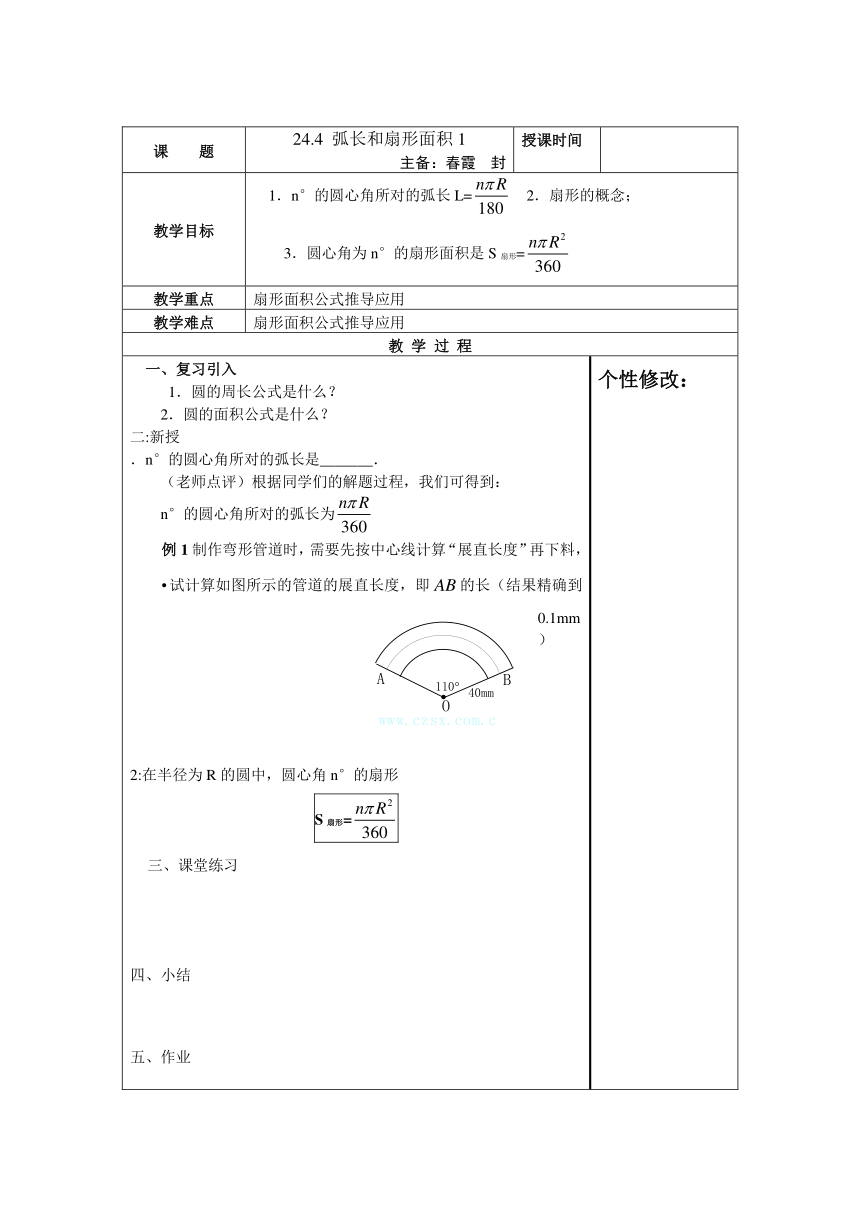 | |
| 格式 | zip | ||
| 文件大小 | 28.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 21:06:34 | ||
图片预览

文档简介
课 题 24.4 弧长和扇形面积1主备:春霞 封 授课时间
教学目标 1.n°的圆心角所对的弧长L= 2.扇形的概念; 3.圆心角为n°的扇形面积是S扇形=
教学重点 扇形面积公式推导应用
教学难点 扇形面积公式推导应用
教 学 过 程
一、复习引入 1.圆的周长公式是什么? 2.圆的面积公式是什么? 二:新授.n°的圆心角所对的弧长是_______. (老师点评)根据同学们的解题过程,我们可得到: n°的圆心角所对的弧长为例1制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即的长(结果精确到0.1mm) 2:在半径为R的圆中,圆心角n°的扇形S扇形= 三、课堂练习四、小结五、作业 个性修改:
教学反思
课 题 24.4 弧长和扇形面积2 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )主备:春霞 封 授课时间
教学目标 了解圆锥母线的概念,理解圆锥侧面积计算公式和应用
教学重点 圆锥侧面积和全面积的计算公式.
教学难点 探索两个公式的由来
教 学 过 程
一、复习引入 1.什么是n°的圆心角所对的弧长和扇形面积的计算公式,并请讲讲它们的异同点. 二、探索新知老师点评:很显然,扇形的半径就是圆锥的母线,扇形的弧长就是圆锥底面圆的周长.因此,要求圆锥的侧面积就是求展开图扇形面积S=,其中n可由2r=求得:n=,∴扇形面积S==rL;全面积是由侧面积和底面圆的面积组成的,所以全面积=rL+r2.例2.已知扇形的圆心角为120°,面积为300cm2. (1)求扇形的弧长; (2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少? 分析:(1)由S扇形=求出R,再代入L=求得.(2)若将此扇形卷成一个圆锥,扇形的弧长就是圆锥底面圆的周长,就可求圆的半径,其截面是一个以底是直径,圆锥母线为腰的等腰三角形.解:(1)如图所示: ∵300= ∴弧长L= HYPERLINK "http://" EMBED Equation.DSMT4 =20(cm)三、课堂练习四、小结五、作业 个性修改:
教学反思
教学目标 1.n°的圆心角所对的弧长L= 2.扇形的概念; 3.圆心角为n°的扇形面积是S扇形=
教学重点 扇形面积公式推导应用
教学难点 扇形面积公式推导应用
教 学 过 程
一、复习引入 1.圆的周长公式是什么? 2.圆的面积公式是什么? 二:新授.n°的圆心角所对的弧长是_______. (老师点评)根据同学们的解题过程,我们可得到: n°的圆心角所对的弧长为例1制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即的长(结果精确到0.1mm) 2:在半径为R的圆中,圆心角n°的扇形S扇形= 三、课堂练习四、小结五、作业 个性修改:
教学反思
课 题 24.4 弧长和扇形面积2 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )主备:春霞 封 授课时间
教学目标 了解圆锥母线的概念,理解圆锥侧面积计算公式和应用
教学重点 圆锥侧面积和全面积的计算公式.
教学难点 探索两个公式的由来
教 学 过 程
一、复习引入 1.什么是n°的圆心角所对的弧长和扇形面积的计算公式,并请讲讲它们的异同点. 二、探索新知老师点评:很显然,扇形的半径就是圆锥的母线,扇形的弧长就是圆锥底面圆的周长.因此,要求圆锥的侧面积就是求展开图扇形面积S=,其中n可由2r=求得:n=,∴扇形面积S==rL;全面积是由侧面积和底面圆的面积组成的,所以全面积=rL+r2.例2.已知扇形的圆心角为120°,面积为300cm2. (1)求扇形的弧长; (2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少? 分析:(1)由S扇形=求出R,再代入L=求得.(2)若将此扇形卷成一个圆锥,扇形的弧长就是圆锥底面圆的周长,就可求圆的半径,其截面是一个以底是直径,圆锥母线为腰的等腰三角形.解:(1)如图所示: ∵300= ∴弧长L= HYPERLINK "http://" EMBED Equation.DSMT4 =20(cm)三、课堂练习四、小结五、作业 个性修改:
教学反思
同课章节目录
