14.2勾股定理的应用 华东师大版初中数学八年级上册同步练习(含解析)
文档属性
| 名称 | 14.2勾股定理的应用 华东师大版初中数学八年级上册同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 510.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 17:52:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
14.2勾股定理的应用华东师大版初中数学八年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处的爬行最短路线长为杯壁厚度不计( )
A. B. C. D.
2.分放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是米分,小红用分钟到家,小颖分钟到家,则小红和小颖家的直线距离为
( )
A. 米 B. 米 C. 米 D. 米
3.如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方形盒子的外表面从点爬行到点,它需要爬行的最短路程为( )
A.
B.
C.
D.
4.年月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的勾股圆方图,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如图,如果大正方形的面积是,小正方形的面积是,直角三角形较短的直角边为,较长的直角边为,那么的值为
( )
A. B. C. D.
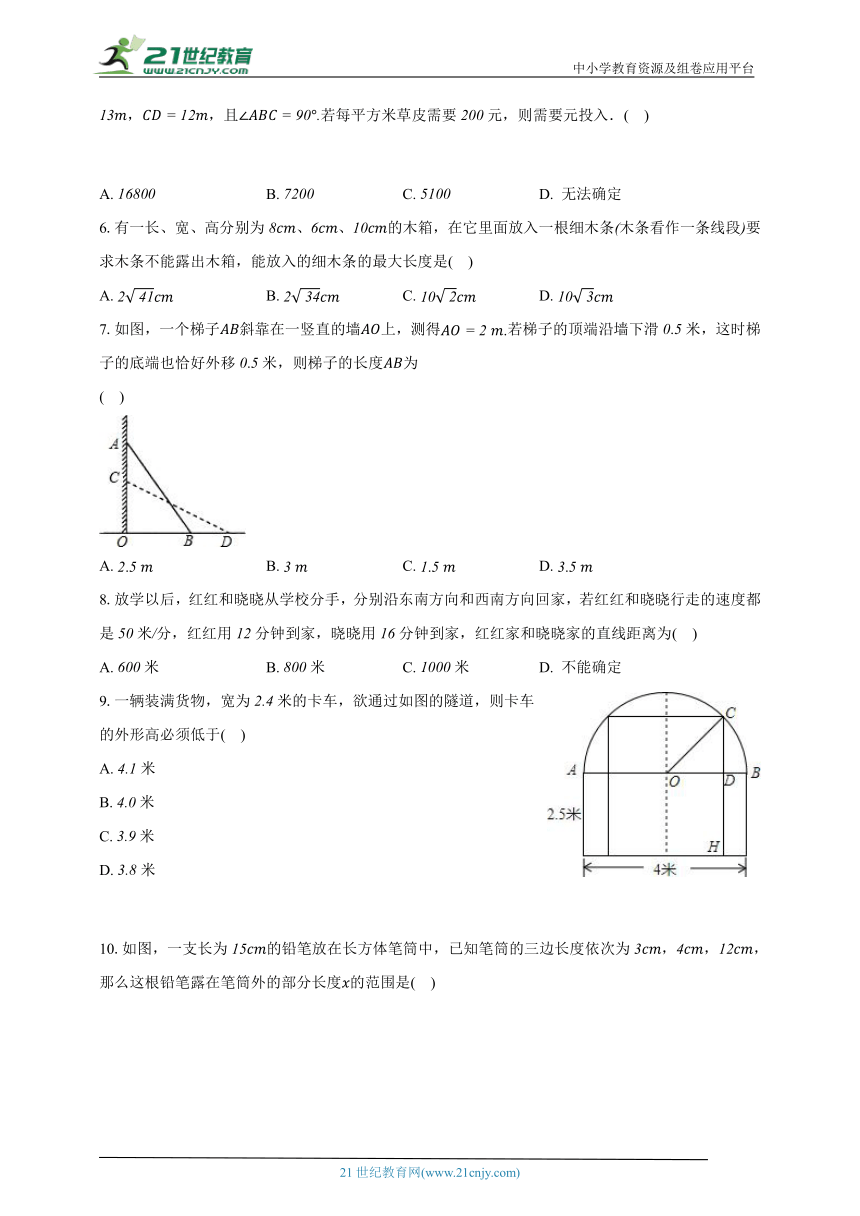
5.如图,在一块四边形空地中植草皮,测得,,,,且若每平方米草皮需要元,则需要元投入.( )
A. B. C. D. 无法确定
6.有一长、宽、高分别为、、的木箱,在它里面放入一根细木条木条看作一条线段要求木条不能露出木箱,能放入的细木条的最大长度是( )
A. B. C. D.
7.如图,一个梯子斜靠在一竖直的墙上,测得若梯子的顶端沿墙下滑米,这时梯子的底端也恰好外移米,则梯子的长度为
( )
A. B. C. D.
8.放学以后,红红和晓晓从学校分手,分别沿东南方向和西南方向回家,若红红和晓晓行走的速度都是米分,红红用分钟到家,晓晓用分钟到家,红红家和晓晓家的直线距离为( )
A. 米 B. 米 C. 米 D. 不能确定
9.一辆装满货物,宽为米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A. 米
B. 米
C. 米
D. 米
10.如图,一支长为的铅笔放在长方体笔筒中,已知笔筒的三边长度依次为,,,那么这根铅笔露在笔筒外的部分长度的范围是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点和点嵌有一圈金属丝,则这圈金属丝的周长最小为______ .
12.如图所示的长方形零件中,,两孔中心,到边上点的距离相等,且,相关尺寸如图所示,则两孔中心,之间的距离为 .
13.如图,一架长的梯子斜靠在竖直的墙上,这时到墙底端的距离为如果梯子的顶端沿墙面下滑,那么点将向外移动 米
14.如图,、、、是四根长度均为的火柴棒,点、、共线.若,,则线段的长度是______.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
在一条东西走向的河流一侧有一村庄,河边原有两个取水点,,其中,由于某种原因,由到的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点、、在同一条直线上,并新修一条路,测得千米,千米,千米.
求证:;
求原来的路线的长;
16.本小题分
如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面多出一段的长度为米,小明同学将绳子拉直,绳子末端落在点处,到旗杆底部的距离为米.
求旗杆的高度;
小明在处,用手拉住绳子的末端,后退至观赛台的米高的台阶上,此时绳子刚好拉直,绳子末端落在点处,问小明需要后退几米即的长?,结果保留位小数
17.本小题分
如图,某中学有一块四边形的空地,学校计划在空地上种植草皮,经测量,,,,若每平方米草皮需要元,问学校需要投入多少资金购买草皮?
18.本小题分
一辆装满快递的物流卡车,其外形为高米,宽米的箱式货车,要开进厂门形状如图所示的工厂,问这辆车能否通过该工厂的厂门厂门上方为半圆形拱门?
19.本小题分
为庆祝“二十大”的召开,园艺工人要在一块直角三角形的草地上种植出如图所示的阴影部分的图案.划出一个三角形后,测得米,米,米,米.求图中阴影部分的面积.
20.本小题分
如图,某小区在施工过程中留下了一块四边形空地,已知米,米,,米,米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米元,试问用该草坪铺满这块空地共需花费多少元?
答案和解析
1.【答案】
【解析】解:如图:
将杯子侧面展开,
作关于的对称点,
则为蚂蚁从外壁处到内壁处的最短距离,即的长度,
,
蚂蚁从外壁处到内壁处的最短距离为,
故选:.
将杯子侧面展开,建立关于的对称点,根据两点之间线段最短可知的长度即为所求.
本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.
2.【答案】
【解析】两人的方向分别是东南方向和西南方向,因而两人的家所在点与学校的连线正好互相垂直,根据勾股定理即可求解.
【解答】解:根据题意得:如图:
米 .
米 .
在直角 中, 米 .
故选: .
【点评】本题考查勾股定理的应用,解题时从实际问题中整理出直角三角形是本题的关键.善于观察题目的信息是解题以及学好数学的关键.
3.【答案】
【解析】解:如图中,,
如图中,,
所以一只蚂蚁要沿着长方形盒子的外表面从点爬行到点,
它需要爬行的最短路程为,
故选:.
此题主要考查了平面展开图的最短路径问题和勾股定理的应用,利用展开图分析得出是解题关键.
4.【答案】
【解析】解:
大正方形的面积四个直角三角形的面积和
.
故选:.
根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积,即四个直角三角形的面积和,从而不难求得.
本题主要考查了完全平方公式的应用,勾股定理的应用,注意完全平方公式的展开:,还要注意图形的面积和,之间的关系.
5.【答案】
【解析】解:连接,
因为,,,,,
所以,
,
,
,
所以,
又因,
,
,
,
,
所以为直角三角形,
因此,
,
,
,
.
故费用为:元,
故选:.
连接,可得与均为直角三角形,进而可求解四边形的面积.
本题考查了勾股定理及勾股定理的逆定理的应用,会用勾股定理逆定理求三角形是直角三角形.
6.【答案】
【解析】解:如图所示:,,,连接,,
由题意可得:在中,
,
在中,
,
故能放入的细木条的最大长度为:.
故选:.
直接利用勾股定理得出,的长,进而得出答案.
此题主要考查了勾股定理的应用,正确构建直角三角形是解题关键.
7.【答案】
【解析】【分析】
本题考查勾股定理的应用,掌握勾股定理是解题关键.
设,则可得,,,利用勾股定理得出,求出的值,再求出即可.
【解答】
解:设,依题意,得,,,
在中,根据勾股定理得
,
在中,根据勾股定理
,
,
解得,
,即,
故梯子的长为,
故选A.
8.【答案】
【解析】解:如图,红红和晓晓行走的速度都是米分,红红用分钟到家,晓晓用分钟到家,
米,米,
在中,
,
米.
故选:.
根据题意画出图形,在中,再利用勾股定理求解即可.
本题考查的是勾股定理的应用,能够准确的画出示意图,把实际问题转换为解直角三角形的问题是解决问题的关键.
9.【答案】
【解析】【分析】
此题主要考查了勾股定理的应用,根据题意得出的长是解题关键.
根据题意欲通过如图的隧道,只要比较距隧道中线米处的高度比车高即可,根据勾股定理得出的长,进而得出的长,即可得出答案.
【解答】
解:车宽米,
欲通过如图的隧道,只要比较距隧道中线米处的高度与车高.
在中,由勾股定理可得:
,
,
米,
卡车的外形高必须低于米.
故选:.
10.【答案】
【解析】【分析】
由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔简外的部分长度最大,最大值为,由勾股定理得,长方体的对角线长为,当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度最小,最小值为,然后作答即可.
本题考查了勾股定理的应用解题的关键在于对知识的熟练掌握.
【解答】
解:由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔筒外的部分长度最大,
最大值为,
由勾股定理得,长方体的对角线长为,
当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度最小,最小值为,
这根铅笔露在笔简外的部分长度的范围是,
故选:.
11.【答案】
【解析】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为的长度.
圆柱底面的周长为,圆柱高为,
,,
,
,
这圈金属丝的周长最小为.
故答案为:.
要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
本题考查了平面展开最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
12.【答案】
【解析】略
13.【答案】
【解析】略
14.【答案】
【解析】解:作,,垂足分别为、,
,
,
,
,
,
,
在和中,
,
≌,
,
,,,
,
,
在中,
由勾股定理得:,
,
,,
,
,
故答案为:.
作,,垂足分别为、,利用证明≌得到,利用勾股定理及等腰三角形的性质求出,
再根据等腰三角形的性质即可得出答案.
本题主要考查了等腰三角形的性质,勾股定理,正确作出辅助线,证得≌是解决问题的关键.
15.【答案】证明:,
,
为直角三角形,
;
设千米,则千米,
,
,
解得:,
答:路线的长为千米.
【解析】利用勾股定理逆定理即可证明;
设千米,则千米,利用勾股定理列出方程,再求解即可.
此题主要考查了勾股定理和勾股定理的逆定理,关键是表示出直角三角形的三边长,利用勾股定理列出方程.
16.【答案】解:设旗杆的高度为米,则为米,
在中,由勾股定理得:,
解得:,
答:旗杆的高度为米;
如图,过作于点,
则四边形是矩形,
米,,
米,
由可知,米,
在中,由勾股定理得:米,
米,
米米,
答:小明需要后退约米.
【解析】设旗杆的高度为米,则为米,在中,由勾股定理得出方程,解方程即可;
过作于点,则四边形是矩形,得米,,再由勾股定理得米,即可解决问题.
本题考查了勾股定理的应用,熟练掌握勾股定理,正确作出辅助线构造直角三角形是解题的关键.
17.【答案】解:连接,
在中,,
在中,,,
而,即,
,
所以需费用元.
【解析】本题考查的是勾股定理的应用、勾股定理的逆定理,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.
连接,在直角三角形中根据勾股定理求得的长,由、、的长度关系可得三角形为直角三角形,则,代入数值计算即可.
18.【答案】解:车宽米,
卡车能否通过,只要比较距厂门中线米处的高度与车高,
在中,由勾股定理可得:
,
,
卡车能通过此门.
【解析】根据勾股定理得出的长,进而得出的长,即可判定.
本题考查勾股定理、矩形的性质、圆等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
19.【答案】解:因为,米,米,
所以米,
因为米,米,
所以,
所以是直角三角形,且,
所以图中阴影部分的面积的面积的面积平方米.
答:图中阴影部分的面积为平方米.
【解析】【分析】
由勾股定理求出米,再由勾股定理的逆定理证出,然后由三角形面积公式求解即可.
【点评】
本题考查了勾股定理以及勾股定理的逆定理的应用,熟练掌握勾股定理和勾股定理的逆定理是解题的关键.
20.【答案】解:如图,连接,
米,米,,
米,平方米,
在中,米,米,米,
,
是直角三角形,且,
平方米,
平方米,
草坪每平方米元,
共需花费元.
答:用该草坪铺满这块空地共需花费元.
【解析】连接,由勾股定理得米,求出平方米,再由勾股定理的逆定理得是直角三角形,且,求出平方米,即可解决问题.
本题考查了勾股定理的应用、勾股定理的逆定理以及三角形面积,熟练掌握勾股定理和勾股定理的逆定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
14.2勾股定理的应用华东师大版初中数学八年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处的爬行最短路线长为杯壁厚度不计( )
A. B. C. D.
2.分放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是米分,小红用分钟到家,小颖分钟到家,则小红和小颖家的直线距离为
( )
A. 米 B. 米 C. 米 D. 米
3.如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方形盒子的外表面从点爬行到点,它需要爬行的最短路程为( )
A.
B.
C.
D.
4.年月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的勾股圆方图,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如图,如果大正方形的面积是,小正方形的面积是,直角三角形较短的直角边为,较长的直角边为,那么的值为
( )
A. B. C. D.
5.如图,在一块四边形空地中植草皮,测得,,,,且若每平方米草皮需要元,则需要元投入.( )
A. B. C. D. 无法确定
6.有一长、宽、高分别为、、的木箱,在它里面放入一根细木条木条看作一条线段要求木条不能露出木箱,能放入的细木条的最大长度是( )
A. B. C. D.
7.如图,一个梯子斜靠在一竖直的墙上,测得若梯子的顶端沿墙下滑米,这时梯子的底端也恰好外移米,则梯子的长度为
( )
A. B. C. D.
8.放学以后,红红和晓晓从学校分手,分别沿东南方向和西南方向回家,若红红和晓晓行走的速度都是米分,红红用分钟到家,晓晓用分钟到家,红红家和晓晓家的直线距离为( )
A. 米 B. 米 C. 米 D. 不能确定
9.一辆装满货物,宽为米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A. 米
B. 米
C. 米
D. 米
10.如图,一支长为的铅笔放在长方体笔筒中,已知笔筒的三边长度依次为,,,那么这根铅笔露在笔筒外的部分长度的范围是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点和点嵌有一圈金属丝,则这圈金属丝的周长最小为______ .
12.如图所示的长方形零件中,,两孔中心,到边上点的距离相等,且,相关尺寸如图所示,则两孔中心,之间的距离为 .
13.如图,一架长的梯子斜靠在竖直的墙上,这时到墙底端的距离为如果梯子的顶端沿墙面下滑,那么点将向外移动 米
14.如图,、、、是四根长度均为的火柴棒,点、、共线.若,,则线段的长度是______.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
在一条东西走向的河流一侧有一村庄,河边原有两个取水点,,其中,由于某种原因,由到的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点、、在同一条直线上,并新修一条路,测得千米,千米,千米.
求证:;
求原来的路线的长;
16.本小题分
如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面多出一段的长度为米,小明同学将绳子拉直,绳子末端落在点处,到旗杆底部的距离为米.
求旗杆的高度;
小明在处,用手拉住绳子的末端,后退至观赛台的米高的台阶上,此时绳子刚好拉直,绳子末端落在点处,问小明需要后退几米即的长?,结果保留位小数
17.本小题分
如图,某中学有一块四边形的空地,学校计划在空地上种植草皮,经测量,,,,若每平方米草皮需要元,问学校需要投入多少资金购买草皮?
18.本小题分
一辆装满快递的物流卡车,其外形为高米,宽米的箱式货车,要开进厂门形状如图所示的工厂,问这辆车能否通过该工厂的厂门厂门上方为半圆形拱门?
19.本小题分
为庆祝“二十大”的召开,园艺工人要在一块直角三角形的草地上种植出如图所示的阴影部分的图案.划出一个三角形后,测得米,米,米,米.求图中阴影部分的面积.
20.本小题分
如图,某小区在施工过程中留下了一块四边形空地,已知米,米,,米,米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米元,试问用该草坪铺满这块空地共需花费多少元?
答案和解析
1.【答案】
【解析】解:如图:
将杯子侧面展开,
作关于的对称点,
则为蚂蚁从外壁处到内壁处的最短距离,即的长度,
,
蚂蚁从外壁处到内壁处的最短距离为,
故选:.
将杯子侧面展开,建立关于的对称点,根据两点之间线段最短可知的长度即为所求.
本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.
2.【答案】
【解析】两人的方向分别是东南方向和西南方向,因而两人的家所在点与学校的连线正好互相垂直,根据勾股定理即可求解.
【解答】解:根据题意得:如图:
米 .
米 .
在直角 中, 米 .
故选: .
【点评】本题考查勾股定理的应用,解题时从实际问题中整理出直角三角形是本题的关键.善于观察题目的信息是解题以及学好数学的关键.
3.【答案】
【解析】解:如图中,,
如图中,,
所以一只蚂蚁要沿着长方形盒子的外表面从点爬行到点,
它需要爬行的最短路程为,
故选:.
此题主要考查了平面展开图的最短路径问题和勾股定理的应用,利用展开图分析得出是解题关键.
4.【答案】
【解析】解:
大正方形的面积四个直角三角形的面积和
.
故选:.
根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积,即四个直角三角形的面积和,从而不难求得.
本题主要考查了完全平方公式的应用,勾股定理的应用,注意完全平方公式的展开:,还要注意图形的面积和,之间的关系.
5.【答案】
【解析】解:连接,
因为,,,,,
所以,
,
,
,
所以,
又因,
,
,
,
,
所以为直角三角形,
因此,
,
,
,
.
故费用为:元,
故选:.
连接,可得与均为直角三角形,进而可求解四边形的面积.
本题考查了勾股定理及勾股定理的逆定理的应用,会用勾股定理逆定理求三角形是直角三角形.
6.【答案】
【解析】解:如图所示:,,,连接,,
由题意可得:在中,
,
在中,
,
故能放入的细木条的最大长度为:.
故选:.
直接利用勾股定理得出,的长,进而得出答案.
此题主要考查了勾股定理的应用,正确构建直角三角形是解题关键.
7.【答案】
【解析】【分析】
本题考查勾股定理的应用,掌握勾股定理是解题关键.
设,则可得,,,利用勾股定理得出,求出的值,再求出即可.
【解答】
解:设,依题意,得,,,
在中,根据勾股定理得
,
在中,根据勾股定理
,
,
解得,
,即,
故梯子的长为,
故选A.
8.【答案】
【解析】解:如图,红红和晓晓行走的速度都是米分,红红用分钟到家,晓晓用分钟到家,
米,米,
在中,
,
米.
故选:.
根据题意画出图形,在中,再利用勾股定理求解即可.
本题考查的是勾股定理的应用,能够准确的画出示意图,把实际问题转换为解直角三角形的问题是解决问题的关键.
9.【答案】
【解析】【分析】
此题主要考查了勾股定理的应用,根据题意得出的长是解题关键.
根据题意欲通过如图的隧道,只要比较距隧道中线米处的高度比车高即可,根据勾股定理得出的长,进而得出的长,即可得出答案.
【解答】
解:车宽米,
欲通过如图的隧道,只要比较距隧道中线米处的高度与车高.
在中,由勾股定理可得:
,
,
米,
卡车的外形高必须低于米.
故选:.
10.【答案】
【解析】【分析】
由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔简外的部分长度最大,最大值为,由勾股定理得,长方体的对角线长为,当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度最小,最小值为,然后作答即可.
本题考查了勾股定理的应用解题的关键在于对知识的熟练掌握.
【解答】
解:由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔筒外的部分长度最大,
最大值为,
由勾股定理得,长方体的对角线长为,
当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度最小,最小值为,
这根铅笔露在笔简外的部分长度的范围是,
故选:.
11.【答案】
【解析】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为的长度.
圆柱底面的周长为,圆柱高为,
,,
,
,
这圈金属丝的周长最小为.
故答案为:.
要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
本题考查了平面展开最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
12.【答案】
【解析】略
13.【答案】
【解析】略
14.【答案】
【解析】解:作,,垂足分别为、,
,
,
,
,
,
,
在和中,
,
≌,
,
,,,
,
,
在中,
由勾股定理得:,
,
,,
,
,
故答案为:.
作,,垂足分别为、,利用证明≌得到,利用勾股定理及等腰三角形的性质求出,
再根据等腰三角形的性质即可得出答案.
本题主要考查了等腰三角形的性质,勾股定理,正确作出辅助线,证得≌是解决问题的关键.
15.【答案】证明:,
,
为直角三角形,
;
设千米,则千米,
,
,
解得:,
答:路线的长为千米.
【解析】利用勾股定理逆定理即可证明;
设千米,则千米,利用勾股定理列出方程,再求解即可.
此题主要考查了勾股定理和勾股定理的逆定理,关键是表示出直角三角形的三边长,利用勾股定理列出方程.
16.【答案】解:设旗杆的高度为米,则为米,
在中,由勾股定理得:,
解得:,
答:旗杆的高度为米;
如图,过作于点,
则四边形是矩形,
米,,
米,
由可知,米,
在中,由勾股定理得:米,
米,
米米,
答:小明需要后退约米.
【解析】设旗杆的高度为米,则为米,在中,由勾股定理得出方程,解方程即可;
过作于点,则四边形是矩形,得米,,再由勾股定理得米,即可解决问题.
本题考查了勾股定理的应用,熟练掌握勾股定理,正确作出辅助线构造直角三角形是解题的关键.
17.【答案】解:连接,
在中,,
在中,,,
而,即,
,
所以需费用元.
【解析】本题考查的是勾股定理的应用、勾股定理的逆定理,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.
连接,在直角三角形中根据勾股定理求得的长,由、、的长度关系可得三角形为直角三角形,则,代入数值计算即可.
18.【答案】解:车宽米,
卡车能否通过,只要比较距厂门中线米处的高度与车高,
在中,由勾股定理可得:
,
,
卡车能通过此门.
【解析】根据勾股定理得出的长,进而得出的长,即可判定.
本题考查勾股定理、矩形的性质、圆等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
19.【答案】解:因为,米,米,
所以米,
因为米,米,
所以,
所以是直角三角形,且,
所以图中阴影部分的面积的面积的面积平方米.
答:图中阴影部分的面积为平方米.
【解析】【分析】
由勾股定理求出米,再由勾股定理的逆定理证出,然后由三角形面积公式求解即可.
【点评】
本题考查了勾股定理以及勾股定理的逆定理的应用,熟练掌握勾股定理和勾股定理的逆定理是解题的关键.
20.【答案】解:如图,连接,
米,米,,
米,平方米,
在中,米,米,米,
,
是直角三角形,且,
平方米,
平方米,
草坪每平方米元,
共需花费元.
答:用该草坪铺满这块空地共需花费元.
【解析】连接,由勾股定理得米,求出平方米,再由勾股定理的逆定理得是直角三角形,且,求出平方米,即可解决问题.
本题考查了勾股定理的应用、勾股定理的逆定理以及三角形面积,熟练掌握勾股定理和勾股定理的逆定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
