3.3.2二次函数解析式与最值问题 课件(共22张PPT)
文档属性
| 名称 | 3.3.2二次函数解析式与最值问题 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 14:45:43 | ||
图片预览








文档简介
(共22张PPT)
二次函数
1. 知识与技能:理解求二次函数解析式的方法及步骤;掌握二次函数解析式的三种形式;
2.过程与方法:通过复习归纳,使自己能够结合所给条件灵活选择二次函数解析式的形式,达到简便运算,提高分析、探索、归纳、概括的能力;
3.情感态度与价值观:让学生经历观察、比较、归纳、应用以及猜想、验证的学习过程,使自己掌握类比、转化等学习数学的方法,养成既能自主探索,又能合作探究的良好学习习惯。
学
目
习
标
复习回顾
PART 01
复习引入
解析式 y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
图象
定义域 R R
值域 [,+ (-,
对称性 函数的图象关于直线x=-对称
1.二次函数的解析式有哪些常用形式?
思考
提示
(1)一般式:y=ax2+bx+c(a≠0);
(2)顶点式:y=a(x-m)2+n(a≠0);
(3)零点式:y=a(x-x1)(x-x2)(a≠0).
题型探究
PART 02
答案 f(x)=x2-4x+3
答案 y=x2-4x+5(答案不唯一)
(2)已知二次函数的图象经过点(4,3),且图象被x轴截得的线段长为2,图象的对称轴为x=2,则二次函数的解析式为________.
例1 (1)二次函数满足下列性质:①定义域为R,值域为[1,+∞);②图象关于x=2对称;请写出函数的一个解析式________.(只要写出一个即可)
求二次函数的解析式
题型一
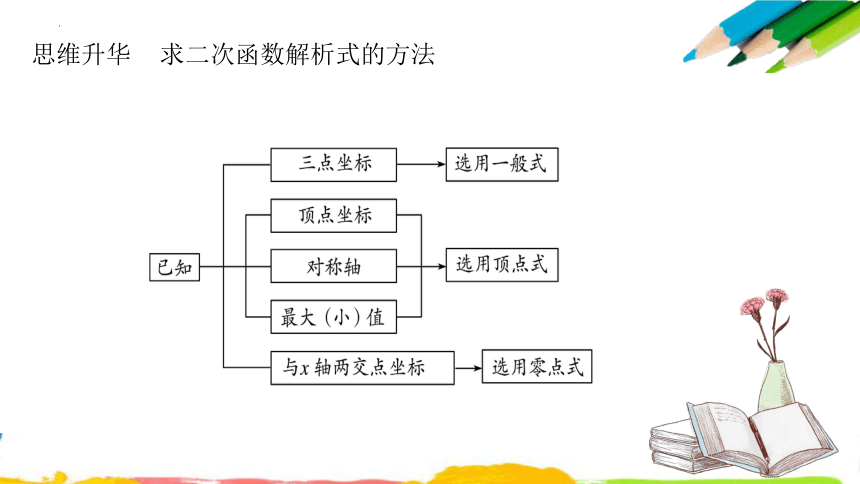
思维升华 求二次函数解析式的方法
跟踪训练1 (1)已知二次函数y=ax2+bx+1(a,b∈R),x∈R,若函数的最小值为f(-1)=0,则函数的解析式为________.
答案 -4x2+4x+7
答案 x2+2x+1
(2)二次函数满足f(2)=f(-1)=-1,且f(x)的最大值是8,则f(x)=________.
命题点1 二次函数的图象
例2 二次函数y=ax2+bx+c的图象如图所示.则下列结论正确的是________.
①b2>4ac;②c>0;③ac>0;④b<0;⑤a-b+c<0.
题型二 二次函数的图象和性质
答案 ①②⑤
二次函数的图象
题型二
例3 已知函数y=ax2+2ax+1在区间[-1,2]上有最大值4,求实数a的值.
解析
命题点2 二次函数的值域、最值
(1)抛物线的开口方向,对称轴位置,定义区间三者相互制约,要注意分类讨论.
(2)要注意数形结合思想的应用,尤其是给定区间上的二次函数最值问题,先“定性”(作草图),再“定量”(看图求解).
(3)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.无论哪种类型,解题的关键都是图象的对称轴与区间的位置关系,当含有参数时,要依据图象的对称轴与区间的位置关系进行分类讨论.
思维升华
解决二次函数图象与性质问题时要注意:
;
跟踪训练2 (1)一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c在同一坐标系中的图象大致是( )
课堂小结
PART 03
课堂小结
解析式 y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
图象
定义域 R R
值域 [,+ (-,
对称性 函数的图象关于直线x=-对称
思维升华 求二次函数解析式的方法
(1)抛物线的开口方向,对称轴位置,定义区间三者相互制约,要注意分类讨论.
(2)要注意数形结合思想的应用,尤其是给定区间上的二次函数最值问题,先“定性”(作草图),再“定量”(看图求解).
(3)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.无论哪种类型,解题的关键都是图象的对称轴与区间的位置关系,当含有参数时,要依据图象的对称轴与区间的位置关系进行分类讨论.
思维升华
解决二次函数图象与性质问题时要注意:
课后作业
PART 04
三、课后习题
1.(多选)已知函数y=3x2-2(m+3)x+m+3的值域为[0,+∞),则实数m的取值范围为( )
A.0 B.[-3,0]
C.3 D.-3
2.已知函数y=x2+ax+b的图象过坐标原点,且满足f(-x)=f(-1+x),则函数f(x)在[-1,3]上的值域为________.
3.已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是___________
4.已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[3,5]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
5.已知函数f(x)=x2+(2a-1)x-3.
(1)当a=2,x∈[-2,3]时,求函数f(x)的值域;
(2)若函数f(x)在[-1,3]上的最大值为1,求实数a的值.
谢谢观看
二次函数
1. 知识与技能:理解求二次函数解析式的方法及步骤;掌握二次函数解析式的三种形式;
2.过程与方法:通过复习归纳,使自己能够结合所给条件灵活选择二次函数解析式的形式,达到简便运算,提高分析、探索、归纳、概括的能力;
3.情感态度与价值观:让学生经历观察、比较、归纳、应用以及猜想、验证的学习过程,使自己掌握类比、转化等学习数学的方法,养成既能自主探索,又能合作探究的良好学习习惯。
学
目
习
标
复习回顾
PART 01
复习引入
解析式 y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
图象
定义域 R R
值域 [,+ (-,
对称性 函数的图象关于直线x=-对称
1.二次函数的解析式有哪些常用形式?
思考
提示
(1)一般式:y=ax2+bx+c(a≠0);
(2)顶点式:y=a(x-m)2+n(a≠0);
(3)零点式:y=a(x-x1)(x-x2)(a≠0).
题型探究
PART 02
答案 f(x)=x2-4x+3
答案 y=x2-4x+5(答案不唯一)
(2)已知二次函数的图象经过点(4,3),且图象被x轴截得的线段长为2,图象的对称轴为x=2,则二次函数的解析式为________.
例1 (1)二次函数满足下列性质:①定义域为R,值域为[1,+∞);②图象关于x=2对称;请写出函数的一个解析式________.(只要写出一个即可)
求二次函数的解析式
题型一
思维升华 求二次函数解析式的方法
跟踪训练1 (1)已知二次函数y=ax2+bx+1(a,b∈R),x∈R,若函数的最小值为f(-1)=0,则函数的解析式为________.
答案 -4x2+4x+7
答案 x2+2x+1
(2)二次函数满足f(2)=f(-1)=-1,且f(x)的最大值是8,则f(x)=________.
命题点1 二次函数的图象
例2 二次函数y=ax2+bx+c的图象如图所示.则下列结论正确的是________.
①b2>4ac;②c>0;③ac>0;④b<0;⑤a-b+c<0.
题型二 二次函数的图象和性质
答案 ①②⑤
二次函数的图象
题型二
例3 已知函数y=ax2+2ax+1在区间[-1,2]上有最大值4,求实数a的值.
解析
命题点2 二次函数的值域、最值
(1)抛物线的开口方向,对称轴位置,定义区间三者相互制约,要注意分类讨论.
(2)要注意数形结合思想的应用,尤其是给定区间上的二次函数最值问题,先“定性”(作草图),再“定量”(看图求解).
(3)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.无论哪种类型,解题的关键都是图象的对称轴与区间的位置关系,当含有参数时,要依据图象的对称轴与区间的位置关系进行分类讨论.
思维升华
解决二次函数图象与性质问题时要注意:
;
跟踪训练2 (1)一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c在同一坐标系中的图象大致是( )
课堂小结
PART 03
课堂小结
解析式 y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
图象
定义域 R R
值域 [,+ (-,
对称性 函数的图象关于直线x=-对称
思维升华 求二次函数解析式的方法
(1)抛物线的开口方向,对称轴位置,定义区间三者相互制约,要注意分类讨论.
(2)要注意数形结合思想的应用,尤其是给定区间上的二次函数最值问题,先“定性”(作草图),再“定量”(看图求解).
(3)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.无论哪种类型,解题的关键都是图象的对称轴与区间的位置关系,当含有参数时,要依据图象的对称轴与区间的位置关系进行分类讨论.
思维升华
解决二次函数图象与性质问题时要注意:
课后作业
PART 04
三、课后习题
1.(多选)已知函数y=3x2-2(m+3)x+m+3的值域为[0,+∞),则实数m的取值范围为( )
A.0 B.[-3,0]
C.3 D.-3
2.已知函数y=x2+ax+b的图象过坐标原点,且满足f(-x)=f(-1+x),则函数f(x)在[-1,3]上的值域为________.
3.已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是___________
4.已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[3,5]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
5.已知函数f(x)=x2+(2a-1)x-3.
(1)当a=2,x∈[-2,3]时,求函数f(x)的值域;
(2)若函数f(x)在[-1,3]上的最大值为1,求实数a的值.
谢谢观看
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
