高中数学人教A版(2019)必修1 第五章三角函数应用章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修1 第五章三角函数应用章节综合练习题(答案+解析) | 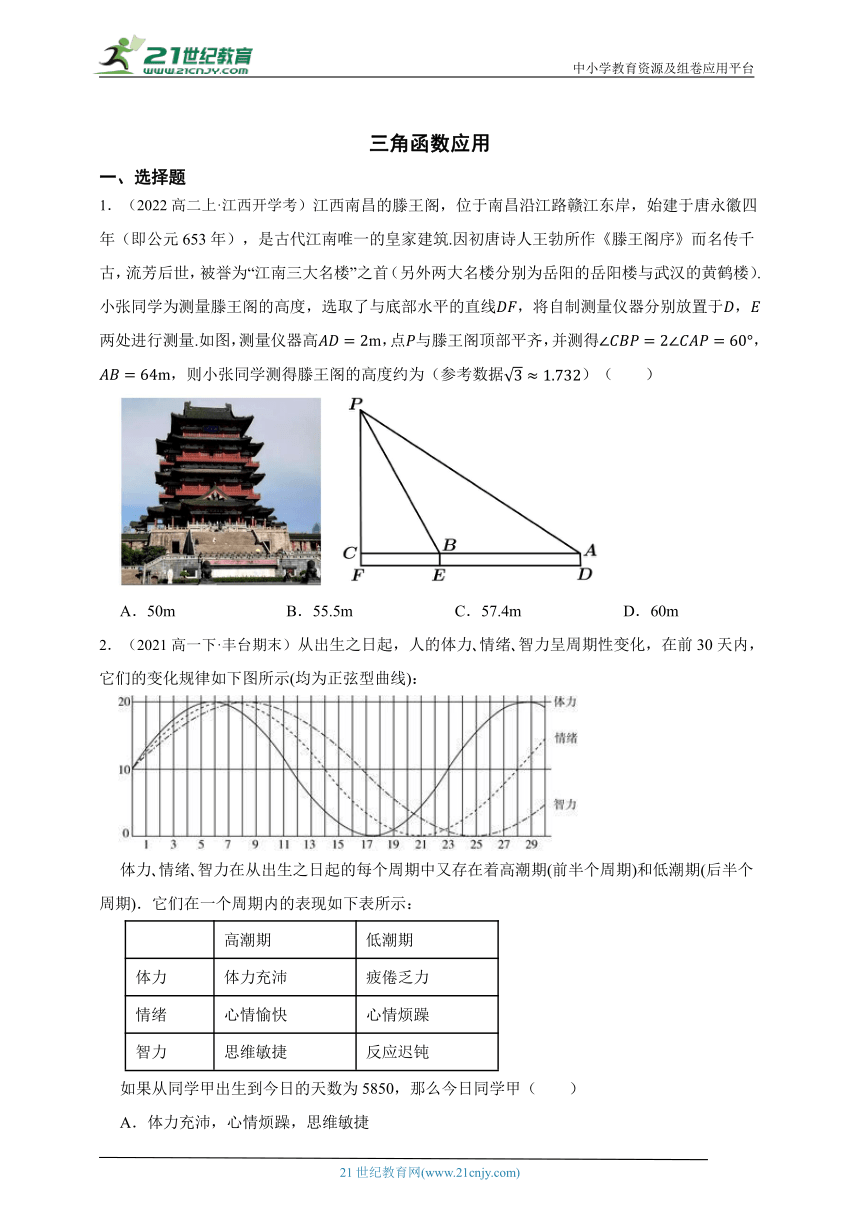 | |
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 20:50:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
三角函数应用
一、选择题
1.(2022高二上·江西开学考)江西南昌的滕王阁,位于南昌沿江路赣江东岸,始建于唐永徽四年(即公元653年),是古代江南唯一的皇家建筑.因初唐诗人王勃所作《滕王阁序》而名传千古,流芳后世,被誉为“江南三大名楼”之首(另外两大名楼分别为岳阳的岳阳楼与武汉的黄鹤楼).小张同学为测量滕王阁的高度,选取了与底部水平的直线,将自制测量仪器分别放置于,两处进行测量.如图,测量仪器高m,点与滕王阁顶部平齐,并测得,m,则小张同学测得滕王阁的高度约为(参考数据)( )
A.50m B.55.5m C.57.4m D.60m
2.(2021高一下·丰台期末)从出生之日起,人的体力 情绪 智力呈周期性变化,在前30天内,它们的变化规律如下图所示(均为正弦型曲线):
体力 情绪 智力在从出生之日起的每个周期中又存在着高潮期(前半个周期)和低潮期(后半个周期).它们在一个周期内的表现如下表所示:
高潮期 低潮期
体力 体力充沛 疲倦乏力
情绪 心情愉快 心情烦躁
智力 思维敏捷 反应迟钝
如果从同学甲出生到今日的天数为5850,那么今日同学甲( )
A.体力充沛,心情烦躁,思维敏捷
B.体力充沛,心情愉快,思维敏捷
C.疲倦乏力,心情愉快,思维敏捷
D.疲倦乏力,心情烦躁,反应迟钝
3.(2023高一下·广东月考)为了研究钟表秒针针尖的运动变化规律,建立如图所示的平面直角坐标系,设秒针针尖位置为点.若初始位置为点,秒针从(规定此时)开始沿顺时针方向转动,若点P的纵坐标为y,,则时t的取值范围为( )
A. B. C. D.
4.(2022高三上·湖北月考)在西双版纳热带植物园中有一种原产于南美热带雨林的时钟花,其花开花谢非常有规律.有研究表明,时钟花开花规律与温度密切相关,时钟花开花所需要的温度约为,但当气温上升到时,时钟花基本都会凋谢.在花期内,时钟花每天开闭一次.已知某景区有时钟花观花区,且该景区6时时的气温(单位:)与时间(单位:小时)近似满足函数关系式,则在6时时中,观花的最佳时段约为( )(参考数据:)
A.6.7时时 B.6.7时时
C.8.7时时 D.8.7时时
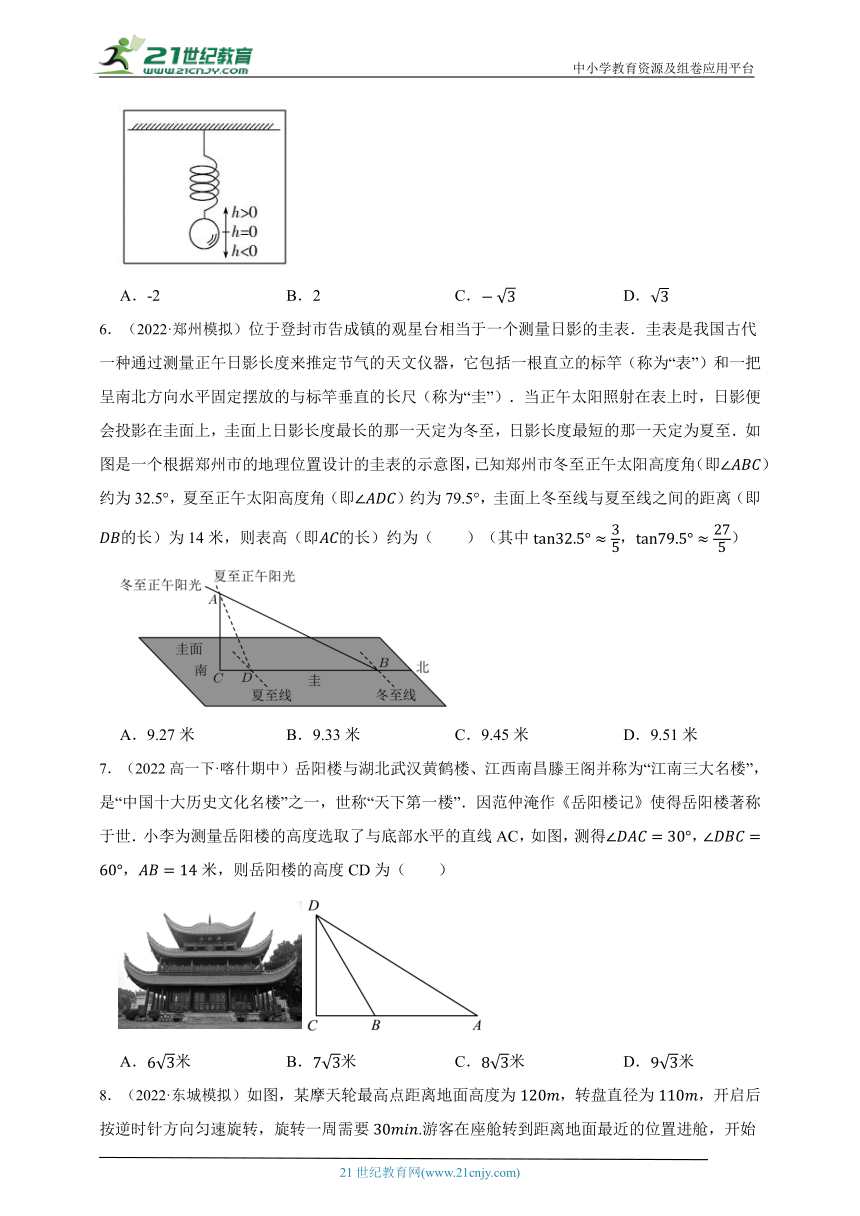
5.(2022高二下·杭州期末)如图,弹簧挂着一个小球作上下运动,小球在t秒时相对于平衡位置的高度h(厘米)由如下关系式确定:,,.已知当时,小球处于平衡位置,并开始向下移动,则小球在秒时h的值为( )
A.-2 B.2 C. D.
6.(2022·郑州模拟)位于登封市告成镇的观星台相当于一个测量日影的圭表.圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”).当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.如图是一个根据郑州市的地理位置设计的圭表的示意图,已知郑州市冬至正午太阳高度角(即)约为32.5°,夏至正午太阳高度角(即)约为79.5°,圭面上冬至线与夏至线之间的距离(即的长)为14米,则表高(即的长)约为( )(其中,)
A.9.27米 B.9.33米 C.9.45米 D.9.51米
7.(2022高一下·喀什期中)岳阳楼与湖北武汉黄鹤楼、江西南昌滕王阁并称为“江南三大名楼”,是“中国十大历史文化名楼”之一,世称“天下第一楼”.因范仲淹作《岳阳楼记》使得岳阳楼著称于世.小李为测量岳阳楼的高度选取了与底部水平的直线AC,如图,测得,,米,则岳阳楼的高度CD为( )
A.米 B.米 C.米 D.米
8.(2022·东城模拟)如图,某摩天轮最高点距离地面高度为,转盘直径为,开启后按逆时针方向匀速旋转,旋转一周需要.游客在座舱转到距离地面最近的位置进舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
9.(2022·吉林模拟)智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声,然后通过主动降噪芯片生成的声波来抵消噪声(如图).已知噪声的声波曲线是,通过主动降噪芯片生成的声波曲线是(其中),则( )
A. B.π C. D.
10.(2022·贵州模拟)2022年春节期间,G市某天从8~16时的温度变化曲线(如图)近似满足函数(,,)的图像.下列说法正确的是( )
A.8~13时这段时间温度逐渐升高
B.8~16时最大温差不超过5℃
C.8~16时0℃以下的时长恰为3小时
D.16时温度为 2℃
11.(2022·重庆市模拟)已知函数,其图象与直线相邻两个交点的距离为,若恒成立,则的取值范围是( )
A. B. C. D.
12.(2022高一上·怀仁期末)已知函数(,,),M是函数图象的一个最高点,K,N是函数图象上与它距离最近的两个对称中心,是边长为1的正三角形,,若函数为偶函数,则的最小值为( )
A. B. C. D.1
13.(2022高一上·平顶山期末)已知函数,,的图象的3个交点可以构成一个等腰直角三角形,则的最小值为( )
A. B. C. D.
14.(2022高一上·武汉期末)如图,摩天轮上一点在时刻距离地面的高度满足,,,,已知某摩天轮的半径为50米,点距地面的高度为60米,摩天轮做匀速运动,每10分钟转一圈,点的起始位置在摩天轮的最低点,则(米)关于(分钟)的解析式为( )
A.() B.()
C.() D.()
15.(2022高一上·海安期末)图1是南北方向、水平放置的圭表(一种度量日影长的天文仪器,由“圭”和“表”两个部件组成)示意图,其中表高为h,日影长为l.图2是地球轴截面的示意图,虚线表示点A处的水平面.已知某测绘兴趣小组在冬至日正午时刻(太阳直射点的纬度为南纬)在某地利用一表高为的圭表按图1方式放置后,测得日影长为,则该地的纬度约为北纬( )(参考数据:,)
A. B. C. D.
16.(2022高三上·吉安期末)如图的曲线就像横放的葫芦的轴截面的边缘线,我们叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它每过相同的间隔振幅就变化一次,且过点,其对应的方程为(,其中为不超过x的最大整数,).若该葫芦曲线上一点N的横坐标为,则点N的纵坐标为( )
A. B. C. D.
17.(2023·静安模拟)摩天轮常被当作一个城市的地标性建筑,如静安大悦城的“Sky Ring”摩天轮是上海首个悬臂式屋顶摩天轮.摩天轮最高点离地面高度106米,转盘直径56米,轮上设置30个极具时尚感的4人轿舱,拥有360度的绝佳视野.游客从离楼顶屋面最近的平台位置进入轿舱,开启后按逆时针匀速旋转t分钟后,游客距离地面的高度为h米,.若在,时刻,游客距离地面的高度相等,则的最小值为( )
A.6 B.12 C.18 D.24
18.(2022·通州模拟)太阳高度角是太阳光线与地面所成的角(即太阳在当地的仰角).设地球表面某地正午太阳高度角为,为此时太阳直射点纬度,为当地纬度值,那么这三个量满足.通州区某校学生科技社团尝试估测通州区当地纬度值(取正值),选择春分当日()测算正午太阳高度角.他们将长度为1米的木杆垂直立于地面,测量木杆的影长.分为甲、乙、丙、丁四个小组在同一场地进行,测量结果如下:
组别 甲组 乙组 丙组 丁组
木杆影长度(米) 0.82 0.80 0.83 0.85
则四组中对通州区当地纬度估测值最大的一组是( )
A.甲组 B.乙组 C.丙组 D.丁组
19.(2022·红河模拟)红河州个旧市是一个风景优美的宜居城市,如图是个旧宝华公园的摩天轮,半径为20米,圆心O距地面的高度为25米,摩天轮运行时按逆时针匀速旋转,转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底,则摩天轮转动一周内具有最佳视觉效果的时间长度(单位:分钟)为( )
A. B.3 C. D.
20.(2021高一下·阎良期末)已知函数,若存在实数、,使得,且,则的最大值为( )
A.9 B.8 C.7 D.5
二、解答题
21.(2023高一下·上饶期末)筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1).如图2,现有一个半径为4米的筒车按逆时针方向每分钟匀速旋转1圈,筒车的轴心距离水面的高度为2米,若以盛水筒刚浮出水面在点处时为初始时刻,设经过秒后盛水筒到水面的距离为(单位:米)(在水面下则为负数).筒车上均匀分布着12个盛水筒,假设盛水筒在最高处时把水倾倒到水槽上.
(1)求函数的表达式;
(2)求第一筒水倾倒的时刻和相邻两个盛水筒倾倒的时间差;
(3)若某一稻田灌溉需水量为100立方米,一个盛水筒倾倒到水槽的水约为0.01立方米,求需要多少小时才能完成该稻田的浇灌.(精确到0.1小时)
22.(2023高一下·苏州期中)如图,一个直径为的水车按逆时针方向每分钟转1.8圈,水车的中心距离水面的高度为,水车上的盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计时,则与时间(单位:)之间的关系为.
(1)求与的函数解析式;
(2)求在一个旋转周期内,盛水筒在水面以上的时长.
23.(2023高一下·南山月考)某游乐场的摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为分钟.在圆周上均匀分布12个座舱,标号分别为(可视为点),现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为分钟.
(1)当时,求1号座舱与地面的距离;
(2)记1号座舱与5号座舱高度之差的绝对值为米,若在这段时间内,恰有三次取得最大值,求的取值范围.
24.(2023高一上·榆林期末)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,所以至今还在农业生产中被使用.如图,假定在水流稳定的情况下,一个直径为10米的筒车开启后按逆时针方向匀速旋转,转一周需要1分钟,筒车的轴心O距离水面的高度为米.以盛水筒P刚浮出水面时开始计算时间,设筒车开始旋转t秒后盛水筒P到水面的距离为h米(规定:若盛水筒P在水面下,则h为负数).
(1)写出h(单位:米)关于t(单位:秒)的函数解析式(其中,,);
(2)若盛水筒P在,时刻距离水面的高度相等,求的最小值.
25.(2023高一上·益阳期末)一个半径为2米的水轮如图所示,水轮圆心O距离水面1米.已知水轮按逆时针作匀速转动,每6秒转一圈,如果当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)以过点O且平行于水轮所在平面与水面的交线L的直线为x轴,以过点O且与水面垂直的直线为y轴,建立如图所示的直角坐标系,试将点P距离水面的高度h(单位:米)表示为时间t(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点P距离水面的高度不低于2米?
26.(2023高一上·增城期末)如图,某地一天从4~18时的温度变化曲线近似满足函数.
(1)求A,b,,;
(2)为响应国家节能减排的号召,建议室温室25℃以上才开空调,求在内,该地适宜开空调的时间段.
27.(2022高一下·湖北期中)天门是一座宜居的城市,城区内北湖公园 陆羽公园 东湖公园是人们休闲娱乐的绝佳去处,尤其是东湖公园的摩天轮,更是让人流连忘返.摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图所示,摩天轮匀速转动一周需要24分钟,其中心距离地面55米,半径为50米,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱.
(1)游客坐上摩天轮的座舱,开始转动分钟后距离地面的高度为H米,求在转动一周的过程中,H关于的函数解析式;
(2)当摩天轮座舱不低于地面高度80米时,游客可以观赏到全园景色.求游客在摩天轮转动一周过程中可观赏到全园景色有多长的时间.
28.(2022高一上·薛城期末)如图,弹簧挂着的小球做上下振动,它在(单位:)时相对于平衡位置(静止时的位置)的高度(单位:)由关系式确定,其中,,.在一次振动中,小球从最高点运动至最低点所用时间为.且最高点与最低点间的距离为.
(1)求小球相对平衡位置的高度(单位:)和时间(单位:)之间的函数关系;
(2)小球在内经过最高点的次数恰为50次,求的取值范围.
29.(2021高一下·东城期末)水车是一种利用水流的动力进行灌溉的工具,工作示意图如图所示.设水车(即圆周)的直径为3米,其中心(即圆心)O到水面的距离b为1.2米,逆时针匀速旋转一圈的时间是80秒.水车边缘上一点P距水面的高度为h(单位;米),水车逆时针旋转时间为t(单位:秒).当点P在水面上时高度记为正值;当点P旋转到水面以下时,点P距水面的高度记为负值.过点P向水面作垂线,交水面于点M,过点O作PM的垂线,交PM于点N.从水车与水面交于点Q时开始计时(t=0),设 ,水车逆时针旋转t秒转动的角的大小记为a.
(1)求f(t)的函数解析式;
(2)当雨季来临时,河流水量增加,点O到水面的距离减少了0.3米,求∠QON的大小(精确到1°);
(3)若水车转速加快到原来的2倍,直接写出f(t)的函数解折式.(参考数据: )
30.(2022高一下·广州期中)已知函数,,如果对于定义域D内的任意实数x,对于给定的非零常数P,总存在非零常数T,恒有成立,则称函数是D上的P级递减周期函数,周期为T;若恒有成立,则称函数是D上的P级周期函数,周期为T.
(1)判断函数是R上的周期为1的2级递减周期函数吗,并说明理由?
(2)已知,是上的P级周期函数,且是上的严格增函数,当时,.求当时,函数的解析式,并求实数P的取值范围;
(3)是否存在非零实数k,使函数是R上的周期为T的T级周期函数?请证明你的结论.
答案解析部分
1.【答案】C
【解析】【解答】在中,,则,在中,,则,,故滕王阁的高度为。
故答案为:C
【分析】利用已知条件结合直角三角形的结构特征和正弦函数的定义,进而得出滕王阁的高度。
2.【答案】A
【解析】【解答】解:由图中数据可知体力的周期为 ,情绪的周期为 ,智力的周期为 .
从同学甲出生到今日的天数为5850,
故对于体力,有 ,处于高潮期,体力充沛;
对于情绪,有 ,处于低潮期,心情烦躁;
对于智力,有 ,处于高潮期,思维敏捷;
故今日同学甲体力充沛,心情烦躁,思维敏捷.
故答案为:A
【分析】 根据题意,由图象分析体力、情绪、智力的周期,由此分析同学甲的状态,即可得答案.
3.【答案】B
【解析】【解答】设y与时间t的函数关系式为,由题意可得,初始位置为,即初相为,故可得,,则,.
又函数周期是60(秒)且秒针按顺时针方向旋转,即,
所以,即,
.
令,则,解得.
故答案为:B
【分析】首先确定函数的周期,设y与时间t的函数关系式为,利用待定系数可求出函数的解析式,进而可求出 时t的取值范围.
4.【答案】C
【解析】【解答】当时,,则在上单调递增.设花开 花谢的时间分别为.
由,得,解得时;
由,得,解得时.
故在6时时中,观花的最佳时段约为8.7时时.
故答案为:C
【分析】先确定在上单调递增.设花开 花谢的时间分别为,再由,求得,.
5.【答案】D
【解析】【解答】因为当时,小球处于平衡位置,并开始向下移动,故,即,又,故,故,故当时,
故答案为:D
【分析】根据当时,小球处于平衡位置,并开始向下移动可求得,进而求得h的解析式,再代入求解即可.
6.【答案】C
【解析】【解答】如图,,
设表高,则由题知,,
所以,
因为,,,
所以,解得,
所以,表高(即的长)约为9.45米.
故答案为:C
【分析】利用已知条件结合正切函数的定义,再结合作差法,进而得出表高。
7.【答案】B
【解析】【解答】因为,,
所以,
所以为等腰三角形,
所以米,
在中,,
所以米.
故答案为:B.
【分析】利用已知条件结合等腰三角形的定义和直角三角形中角的关系式,从而结合余弦函数的定义,进而得出岳阳楼的高度CD的长。
8.【答案】B
【解析】【解答】解:根据题意设,,
因为某摩天轮最高点距离地面高度为,转盘直径为,
所以,该摩天轮最低点距离地面高度为,
所以,解得,
因为开启后按逆时针方向匀速旋转,旋转一周需要,
所以,,解得,
因为时,,故,即,解得.
所以,
故答案为:B
【分析】根据题意,设,进而结合题意求解即可.
9.【答案】C
【解析】【解答】由于抵消噪声,所以振幅没有改变,周期没有改变,即,,
即,要想抵消噪声,需要主动降噪芯片生成的声波曲线是,
即,
因为,所以令,即,
故答案为:C
【分析】 根据题意可得通过主动降噪芯片生成的声波曲线是,从而可求φ的值.
10.【答案】D
【解析】【解答】由图像可知:8~13时这段时间温度先下降再升高,A不符合题意;
8~16时最大温度℃,最小温度℃,最大温差为℃,B不符合题意;
8~16时0℃以下的时长超过3小时,C不符合题意;
T=4×(13 11)=8=2πω,ω=π4,又过点(13,22),故22cos(π4 13+φ)=22,解得φ=3π4,
故f(x)=22cos(π4x+3π4),f(16)=22cos(π4 16+3π4)= 2,故16时温度为 2℃,D符合题意.
故答案为:D.
【分析】由图像直接判断A、B、C选项,求出解析式判断D选项即可.
11.【答案】D
【解析】【解答】解:函数 ,其图象与直线 相邻两个交点的距离为 ,
故函数的周期为 ,故 ,
若 对 恒成立,即当 时, 恒成立,
所以 ,解得
因为 ,所以 .
故答案为:D.
【分析】由题意可得函数的周期为 ,求得 .再根据当 时 恒成立,即 ,再结合 求得 的取值范围.
12.【答案】B
【解析】【解答】解:因为M是函数图像的一个最高点,K,N是函数图象上与它距离最近的两个对称中心,
又因为是边长为1的正三角形,
所以正三角形的高是点 的纵坐标,即,
所以,,即,
又因为,所以,
因为,所以.故.
因为函数为偶函数,所以,,
所以当时,最小为.
故答案为:B.
【分析】根据题意结合周期的公式即可求出的值,再由特殊点法代入计算出,由此即可得出函数的解析式,再结合正弦函数的图象和性质,正弦函数的周期公式以及单调性结合整体思想即可得出结果,然后对k赋值计算出结果即可。
13.【答案】C
【解析】【解答】令和相等可得,即;
此时,即等腰直角三角形的斜边上的高为,所以底边长为,
令底边的一个端点为,则另一个端点为,
所以,即,
当时,的最小值,最小值为
故答案为:C.
【分析】先根据函数值相等求出,可得,由此可知等腰直角三角形的斜边上的高为,所以底边长为,令底边的一个端点为,则另一个端点为,由此可知,可得,据此即可求出结果.
14.【答案】B
【解析】【解答】因函数最大值为110,最小值为10,因此有,解得,
而函数的周期为10,即,则,
又当时,,则,而,解得,
所以。
故答案为:B
【分析】利用已知条件结合正弦型函数的最值求解方法,进而得出A,B的值,再利用正弦型函数的最小正周期公式得出的值,再结合五点对应法和,进而得出的值,从而得出 (米)关于(分钟)的解析式 。
15.【答案】B
【解析】【解答】由图1可得,又,
所以,所以,
所以,
该地的纬度约为北纬。
故答案为:B.
【分析】利用已知条件结合正切函数的定义和角之间的关系,进而得出该地的纬度约为北纬的度数。
16.【答案】D
【解析】【解答】解:由题意,因为()过点,
所以,
所以,所以,即,
又,所以,所以,
所以当时,,所以,
点N的纵坐标为,
故答案为:D.
【分析】将点代入方程,求出,然后利用已知条件求出,从而将代入方程即可求解.
17.【答案】B
【解析】【解答】由可知,
当时,,
当时,,
若在,时刻,游客距离地面的高度相等,
则由对称性可知此时的最小值为.
故答案为:B.
【分析】由结合余弦型函数的图象求最值的方法得出h的最小值,若在,时刻,游客距离地面的高度相等,则由对称性可知此时的最小值。
18.【答案】D
【解析】【解答】如图所示,
地球表面某地正午太阳高度角为,为此时太阳直射点纬度,为当地纬度值,那么这三个量满足,
当且为正值,可得,即,
设木杆的影长为,可得,
因为甲、乙、丙、丁四个小组在同一场地进行,得到影长分别为,
所以当时,取得最小值,此时求得最大值,
所以四组中对通州区当地纬度估测值最大的一组是丁组.
故答案为:D.
【分析】利用已知条件结合正切函数的定义和正切函数的图象求角的最值的方法,进而得出四组中对通州区当地纬度估测值最大的一组。
19.【答案】C
【解析】【解答】设点P距离地面高度h与时间t的函数解析式为,
由题意,得,,,
所以,
又因为,所以,
所以,
令,即,
故,即在摩天轮转动的一圈内,
有分钟会有这种最佳视觉效果。
故答案为:C.
【分析】利用已知条件求出函数的解析式为,令,从而解不等式组求出t的取值范围,进而得出在摩天轮转动的一圈内具有最佳视觉效果的时间长度。
20.【答案】A
【解析】【解答】因为,,
所以,,
,即,,
,即,,
则,
因为,所以,,
因为,所以的最大值为9。
故答案为:A.
【分析】利用已知条件结合作差法和代入法得出和,进而得出,再利用得出,再结合,进而得出的最大值。
21.【答案】(1)解:由已知可得,
∵盛水筒运动的角速度,
∴秒后盛水筒转过的角度为,
此时可得以为终边的角
∴
(2)解:当第一筒水到达最高位置时,是第一次取得最大值,此时,得(秒),
相邻两个盛水筒倾倒的时间差为(秒),
(3)解:完成该稻田的浇灌需倾倒筒水,
所需时间为秒,约为13.9小时.
所以第一筒水倾倒的时刻为20秒,相邻两个盛水筒倾倒的时间差为5秒,约13.9小时可完成该稻田的浇灌.
【解析】【分析】(1)根据题意结合任意角三角函数的定义分析求解;
(2)结合三角函数的周期运算求解;
(3)根据题意运算求解即可.
22.【答案】(1)解:依题意,, ,即,则,
由给定的图形知,,又,即有,
所以与的函数解析式是;
(2)解:令,即
所以,解得,
所以水车在一个旋转周期内,盛水筒在水面以上的时长为.
【解析】【分析】(1)结合图形,可确定 与的函数解析式;
(2) 令 ,利用正弦函数的性质可求出t的范围,进而得盛水筒在水面以上的时长.
23.【答案】(1)解:设座舱与地面的距离与时间的函数关系的解析式为
,,,,则,,
,依题意,,
当时,,,
取,,
,当时,1号舱与地面的距离为;
(2)解:依题意,,
,
令,,解得,,
当,时,取得最大值,故,
即,即的取值范围是.
【解析】【分析】(1) 设座舱与地面的距离与时间的函数关系的解析式为,,,,根据所给条件,求出A,b,,,即可得到函数解析式,再令t=6代入计算求出 1号座舱与地面的距离;
(2)依题意可得h1 , h5 ,从而得到高度差函数 ,利用两角和差的正弦公式化简,再结合正弦函数的性质求出函数取得最大值时t的值,即可求解出 的取值范围.
24.【答案】(1)解:如图,过O作交PB于点C,设筒车与水面的交点为M,N,连接OM.
因为筒车转一周需要1分钟,所以筒车每秒钟转,则.
又因为,,所以,
则.
,,
即,.
(2)解:不妨设,由题意得,
故,
①,,解得,,故,当且仅当,时,等号成立,
②,,解得,显然当时,取得最小值,最小值为.
综上,的最小值为40.
【解析】【分析】 (1)过O作交PB于点C,设筒车与水面的交点为M,N,连接OM,根据已知条件易知,又因为,,得,根据即可求得函数的解析式;
(2) 不妨设,由题意得, 即分两种情况讨论,计算即可.
25.【答案】(1)解:设,
根据函数的物理意义可知:
,
由题意可知当时,,
则,所以,
则,
又因为函数的最小正周期为,
所以,
所以;
(2)解:根据题意可知,,
即,
当水轮转动一圈时,,,
可得:,
所以此时,
解得,
又因为 (秒,
即水轮转动任意一圈内,有秒的时间点距水面的高度不低于2米.
【解析】【分析】(1)首先设出函数的解析式,然后结合题意和物理意义及待定系数法确定参数值即可求得函数的解析式;
(2)结合(1)中函数的解析式求解三角不等式即可确定有多长时间点P距离水面的高度不低于2米.
26.【答案】(1)解:根据图象,,,
∵,∴,
由当,,解得.
(2)解:由(1)得,,
∵,则,由,即,得.
故.
∴适宜开空调的时间段为
【解析】【分析】(1)利用已知条件结合余弦型函数的部分图象,再结合函数的最高点的纵坐标和对称轴的位置,进而得出 A,b的值,再结合余弦型函数的最小正周期公式得出的值,再利用五点对应法和的取值范围,进而得出的值。
(2)利用(1)求出函数的解析式,再利用余弦型函数的图象额已知条件,进而得出适宜开空调的时间段。
27.【答案】(1)解:如图设座舱距离地面最近的位置为点P,以轴心为原点,与地面平行的直线为轴建立直角坐标系.
设时,游客上座舱时位于点,
根据摩天轮转一周大约需要24min,可知座舱转动的角速度约为,由题意可得
,.
(2)解:时,满足题意.
解得,,
令,解得
又因为,故,则.
所以
游客在摩天轮转动一周过程中可观赏到全园景色的时间为8分钟.
【解析】【分析】 (1)设座舱距离地面最近的位置为点P,以轴心为原点,与地面平行的直线为轴建立直角坐标系,设时,游客上座舱时位于点,根据摩天轮转一周大约需要24min,可知座舱转动的角速度,由题意可得在转动一周的过程中,H关于的函数解析式。
(2)利用已知条件得出时,进而得出,再结合正弦型函数的图象和,进而得出t的取值范围,从而得出游客在摩天轮转动一周过程中可观赏到全园景色的时间。
28.【答案】(1)解:因为小球振动过程中最高点与最低点的距离为,所以.
因为在一次振动中,小球从最高点运动至最低点所用时间为,所以周期为2,
即,所以.
所以,.
(2)解:由题意,当时,小球第一次到达最高点,
以后每隔一个周期都出现一次最高点,
因为小球在内经过最高点的次数恰为50次,
所以.
因为,所以,
所以的取值范围为.
(注:的取值范围不考虑开闭)
【解析】【分析】(1)首先根据题意得到,,从而得到 ,;
(2)根据题意,当时,小球第一次到达最高点,从而得到,再根据周期为2,即可得到.
29.【答案】(1)由题意设 ,则 , ,则 ,
由题意 , 是锐角,所以 ,
, , ,
所以 ;
(2)河水上涨 米,在 中, , .
(3)水车转速加快到原来的2倍,则周期变为原来的一半,即 , ,
所以 .
【解析】【分析】(1)利用已知条件结合正弦型函数的最高点的纵坐标求出A的值,再利用正弦型函数的最小正周期公式求出的值,再利用特殊点法,进而结合的取值范围,从而求出的值,进而求出正弦型函数f(t)的解析式。
(2)利用已知条件结合正弦函数的定义,进而求出 ∠QON的大小。
(3)利用水车转速加快到原来的2倍,则周期变为原来的一半,从而求出正弦型函数的最小正周期,再利用正弦型函数的最小正周期公式,进而求出的值,进而求出函数f(t)的解析式。
30.【答案】(1)解:依题意,函数定义域是R,
,
即,成立,
所以函数是R上的周期为1的2级递减周期函数.
(2)解:因,是上的P级周期函数,则,即,
而当时,,当时,,,
当时,,则,
当时,,则,
……
当时,,则,
并且有:当时,,当时,,当时,,……,
当时,,
因是上的严格增函数,则有,解得,
所以当时,,且.
(3)解:假定存在非零实数k,使函数是R上的周期为T的T级周期函数,
即,恒有成立,则,恒有成立,
即,恒有成立,当时,,则,,
于是得,,要使恒成立,则有,
当,即时,由函数与的图象存在交点知,方程有解,
此时恒成立,则,即,
当,即时,由函数与的图象没有交点知,方程无解,
所以存在,符合题意,其中满足.
【解析】【分析】(1) 根据题意,化简,进而得到是R上的周期为1的2级递减周期函数;
(2) 根据题意得到,根据三角函数的性质,分类讨论,即可求得数的解析式,并求实数P的取值范围;
(3) 根据题意转化为,恒有成立,要使恒成立,得到,分和,两种情况讨论,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
三角函数应用
一、选择题
1.(2022高二上·江西开学考)江西南昌的滕王阁,位于南昌沿江路赣江东岸,始建于唐永徽四年(即公元653年),是古代江南唯一的皇家建筑.因初唐诗人王勃所作《滕王阁序》而名传千古,流芳后世,被誉为“江南三大名楼”之首(另外两大名楼分别为岳阳的岳阳楼与武汉的黄鹤楼).小张同学为测量滕王阁的高度,选取了与底部水平的直线,将自制测量仪器分别放置于,两处进行测量.如图,测量仪器高m,点与滕王阁顶部平齐,并测得,m,则小张同学测得滕王阁的高度约为(参考数据)( )
A.50m B.55.5m C.57.4m D.60m
2.(2021高一下·丰台期末)从出生之日起,人的体力 情绪 智力呈周期性变化,在前30天内,它们的变化规律如下图所示(均为正弦型曲线):
体力 情绪 智力在从出生之日起的每个周期中又存在着高潮期(前半个周期)和低潮期(后半个周期).它们在一个周期内的表现如下表所示:
高潮期 低潮期
体力 体力充沛 疲倦乏力
情绪 心情愉快 心情烦躁
智力 思维敏捷 反应迟钝
如果从同学甲出生到今日的天数为5850,那么今日同学甲( )
A.体力充沛,心情烦躁,思维敏捷
B.体力充沛,心情愉快,思维敏捷
C.疲倦乏力,心情愉快,思维敏捷
D.疲倦乏力,心情烦躁,反应迟钝
3.(2023高一下·广东月考)为了研究钟表秒针针尖的运动变化规律,建立如图所示的平面直角坐标系,设秒针针尖位置为点.若初始位置为点,秒针从(规定此时)开始沿顺时针方向转动,若点P的纵坐标为y,,则时t的取值范围为( )
A. B. C. D.
4.(2022高三上·湖北月考)在西双版纳热带植物园中有一种原产于南美热带雨林的时钟花,其花开花谢非常有规律.有研究表明,时钟花开花规律与温度密切相关,时钟花开花所需要的温度约为,但当气温上升到时,时钟花基本都会凋谢.在花期内,时钟花每天开闭一次.已知某景区有时钟花观花区,且该景区6时时的气温(单位:)与时间(单位:小时)近似满足函数关系式,则在6时时中,观花的最佳时段约为( )(参考数据:)
A.6.7时时 B.6.7时时
C.8.7时时 D.8.7时时
5.(2022高二下·杭州期末)如图,弹簧挂着一个小球作上下运动,小球在t秒时相对于平衡位置的高度h(厘米)由如下关系式确定:,,.已知当时,小球处于平衡位置,并开始向下移动,则小球在秒时h的值为( )
A.-2 B.2 C. D.
6.(2022·郑州模拟)位于登封市告成镇的观星台相当于一个测量日影的圭表.圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”).当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.如图是一个根据郑州市的地理位置设计的圭表的示意图,已知郑州市冬至正午太阳高度角(即)约为32.5°,夏至正午太阳高度角(即)约为79.5°,圭面上冬至线与夏至线之间的距离(即的长)为14米,则表高(即的长)约为( )(其中,)
A.9.27米 B.9.33米 C.9.45米 D.9.51米
7.(2022高一下·喀什期中)岳阳楼与湖北武汉黄鹤楼、江西南昌滕王阁并称为“江南三大名楼”,是“中国十大历史文化名楼”之一,世称“天下第一楼”.因范仲淹作《岳阳楼记》使得岳阳楼著称于世.小李为测量岳阳楼的高度选取了与底部水平的直线AC,如图,测得,,米,则岳阳楼的高度CD为( )
A.米 B.米 C.米 D.米
8.(2022·东城模拟)如图,某摩天轮最高点距离地面高度为,转盘直径为,开启后按逆时针方向匀速旋转,旋转一周需要.游客在座舱转到距离地面最近的位置进舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
9.(2022·吉林模拟)智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声,然后通过主动降噪芯片生成的声波来抵消噪声(如图).已知噪声的声波曲线是,通过主动降噪芯片生成的声波曲线是(其中),则( )
A. B.π C. D.
10.(2022·贵州模拟)2022年春节期间,G市某天从8~16时的温度变化曲线(如图)近似满足函数(,,)的图像.下列说法正确的是( )
A.8~13时这段时间温度逐渐升高
B.8~16时最大温差不超过5℃
C.8~16时0℃以下的时长恰为3小时
D.16时温度为 2℃
11.(2022·重庆市模拟)已知函数,其图象与直线相邻两个交点的距离为,若恒成立,则的取值范围是( )
A. B. C. D.
12.(2022高一上·怀仁期末)已知函数(,,),M是函数图象的一个最高点,K,N是函数图象上与它距离最近的两个对称中心,是边长为1的正三角形,,若函数为偶函数,则的最小值为( )
A. B. C. D.1
13.(2022高一上·平顶山期末)已知函数,,的图象的3个交点可以构成一个等腰直角三角形,则的最小值为( )
A. B. C. D.
14.(2022高一上·武汉期末)如图,摩天轮上一点在时刻距离地面的高度满足,,,,已知某摩天轮的半径为50米,点距地面的高度为60米,摩天轮做匀速运动,每10分钟转一圈,点的起始位置在摩天轮的最低点,则(米)关于(分钟)的解析式为( )
A.() B.()
C.() D.()
15.(2022高一上·海安期末)图1是南北方向、水平放置的圭表(一种度量日影长的天文仪器,由“圭”和“表”两个部件组成)示意图,其中表高为h,日影长为l.图2是地球轴截面的示意图,虚线表示点A处的水平面.已知某测绘兴趣小组在冬至日正午时刻(太阳直射点的纬度为南纬)在某地利用一表高为的圭表按图1方式放置后,测得日影长为,则该地的纬度约为北纬( )(参考数据:,)
A. B. C. D.
16.(2022高三上·吉安期末)如图的曲线就像横放的葫芦的轴截面的边缘线,我们叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它每过相同的间隔振幅就变化一次,且过点,其对应的方程为(,其中为不超过x的最大整数,).若该葫芦曲线上一点N的横坐标为,则点N的纵坐标为( )
A. B. C. D.
17.(2023·静安模拟)摩天轮常被当作一个城市的地标性建筑,如静安大悦城的“Sky Ring”摩天轮是上海首个悬臂式屋顶摩天轮.摩天轮最高点离地面高度106米,转盘直径56米,轮上设置30个极具时尚感的4人轿舱,拥有360度的绝佳视野.游客从离楼顶屋面最近的平台位置进入轿舱,开启后按逆时针匀速旋转t分钟后,游客距离地面的高度为h米,.若在,时刻,游客距离地面的高度相等,则的最小值为( )
A.6 B.12 C.18 D.24
18.(2022·通州模拟)太阳高度角是太阳光线与地面所成的角(即太阳在当地的仰角).设地球表面某地正午太阳高度角为,为此时太阳直射点纬度,为当地纬度值,那么这三个量满足.通州区某校学生科技社团尝试估测通州区当地纬度值(取正值),选择春分当日()测算正午太阳高度角.他们将长度为1米的木杆垂直立于地面,测量木杆的影长.分为甲、乙、丙、丁四个小组在同一场地进行,测量结果如下:
组别 甲组 乙组 丙组 丁组
木杆影长度(米) 0.82 0.80 0.83 0.85
则四组中对通州区当地纬度估测值最大的一组是( )
A.甲组 B.乙组 C.丙组 D.丁组
19.(2022·红河模拟)红河州个旧市是一个风景优美的宜居城市,如图是个旧宝华公园的摩天轮,半径为20米,圆心O距地面的高度为25米,摩天轮运行时按逆时针匀速旋转,转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底,则摩天轮转动一周内具有最佳视觉效果的时间长度(单位:分钟)为( )
A. B.3 C. D.
20.(2021高一下·阎良期末)已知函数,若存在实数、,使得,且,则的最大值为( )
A.9 B.8 C.7 D.5
二、解答题
21.(2023高一下·上饶期末)筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1).如图2,现有一个半径为4米的筒车按逆时针方向每分钟匀速旋转1圈,筒车的轴心距离水面的高度为2米,若以盛水筒刚浮出水面在点处时为初始时刻,设经过秒后盛水筒到水面的距离为(单位:米)(在水面下则为负数).筒车上均匀分布着12个盛水筒,假设盛水筒在最高处时把水倾倒到水槽上.
(1)求函数的表达式;
(2)求第一筒水倾倒的时刻和相邻两个盛水筒倾倒的时间差;
(3)若某一稻田灌溉需水量为100立方米,一个盛水筒倾倒到水槽的水约为0.01立方米,求需要多少小时才能完成该稻田的浇灌.(精确到0.1小时)
22.(2023高一下·苏州期中)如图,一个直径为的水车按逆时针方向每分钟转1.8圈,水车的中心距离水面的高度为,水车上的盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计时,则与时间(单位:)之间的关系为.
(1)求与的函数解析式;
(2)求在一个旋转周期内,盛水筒在水面以上的时长.
23.(2023高一下·南山月考)某游乐场的摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为分钟.在圆周上均匀分布12个座舱,标号分别为(可视为点),现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为分钟.
(1)当时,求1号座舱与地面的距离;
(2)记1号座舱与5号座舱高度之差的绝对值为米,若在这段时间内,恰有三次取得最大值,求的取值范围.
24.(2023高一上·榆林期末)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,所以至今还在农业生产中被使用.如图,假定在水流稳定的情况下,一个直径为10米的筒车开启后按逆时针方向匀速旋转,转一周需要1分钟,筒车的轴心O距离水面的高度为米.以盛水筒P刚浮出水面时开始计算时间,设筒车开始旋转t秒后盛水筒P到水面的距离为h米(规定:若盛水筒P在水面下,则h为负数).
(1)写出h(单位:米)关于t(单位:秒)的函数解析式(其中,,);
(2)若盛水筒P在,时刻距离水面的高度相等,求的最小值.
25.(2023高一上·益阳期末)一个半径为2米的水轮如图所示,水轮圆心O距离水面1米.已知水轮按逆时针作匀速转动,每6秒转一圈,如果当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)以过点O且平行于水轮所在平面与水面的交线L的直线为x轴,以过点O且与水面垂直的直线为y轴,建立如图所示的直角坐标系,试将点P距离水面的高度h(单位:米)表示为时间t(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点P距离水面的高度不低于2米?
26.(2023高一上·增城期末)如图,某地一天从4~18时的温度变化曲线近似满足函数.
(1)求A,b,,;
(2)为响应国家节能减排的号召,建议室温室25℃以上才开空调,求在内,该地适宜开空调的时间段.
27.(2022高一下·湖北期中)天门是一座宜居的城市,城区内北湖公园 陆羽公园 东湖公园是人们休闲娱乐的绝佳去处,尤其是东湖公园的摩天轮,更是让人流连忘返.摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图所示,摩天轮匀速转动一周需要24分钟,其中心距离地面55米,半径为50米,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱.
(1)游客坐上摩天轮的座舱,开始转动分钟后距离地面的高度为H米,求在转动一周的过程中,H关于的函数解析式;
(2)当摩天轮座舱不低于地面高度80米时,游客可以观赏到全园景色.求游客在摩天轮转动一周过程中可观赏到全园景色有多长的时间.
28.(2022高一上·薛城期末)如图,弹簧挂着的小球做上下振动,它在(单位:)时相对于平衡位置(静止时的位置)的高度(单位:)由关系式确定,其中,,.在一次振动中,小球从最高点运动至最低点所用时间为.且最高点与最低点间的距离为.
(1)求小球相对平衡位置的高度(单位:)和时间(单位:)之间的函数关系;
(2)小球在内经过最高点的次数恰为50次,求的取值范围.
29.(2021高一下·东城期末)水车是一种利用水流的动力进行灌溉的工具,工作示意图如图所示.设水车(即圆周)的直径为3米,其中心(即圆心)O到水面的距离b为1.2米,逆时针匀速旋转一圈的时间是80秒.水车边缘上一点P距水面的高度为h(单位;米),水车逆时针旋转时间为t(单位:秒).当点P在水面上时高度记为正值;当点P旋转到水面以下时,点P距水面的高度记为负值.过点P向水面作垂线,交水面于点M,过点O作PM的垂线,交PM于点N.从水车与水面交于点Q时开始计时(t=0),设 ,水车逆时针旋转t秒转动的角的大小记为a.
(1)求f(t)的函数解析式;
(2)当雨季来临时,河流水量增加,点O到水面的距离减少了0.3米,求∠QON的大小(精确到1°);
(3)若水车转速加快到原来的2倍,直接写出f(t)的函数解折式.(参考数据: )
30.(2022高一下·广州期中)已知函数,,如果对于定义域D内的任意实数x,对于给定的非零常数P,总存在非零常数T,恒有成立,则称函数是D上的P级递减周期函数,周期为T;若恒有成立,则称函数是D上的P级周期函数,周期为T.
(1)判断函数是R上的周期为1的2级递减周期函数吗,并说明理由?
(2)已知,是上的P级周期函数,且是上的严格增函数,当时,.求当时,函数的解析式,并求实数P的取值范围;
(3)是否存在非零实数k,使函数是R上的周期为T的T级周期函数?请证明你的结论.
答案解析部分
1.【答案】C
【解析】【解答】在中,,则,在中,,则,,故滕王阁的高度为。
故答案为:C
【分析】利用已知条件结合直角三角形的结构特征和正弦函数的定义,进而得出滕王阁的高度。
2.【答案】A
【解析】【解答】解:由图中数据可知体力的周期为 ,情绪的周期为 ,智力的周期为 .
从同学甲出生到今日的天数为5850,
故对于体力,有 ,处于高潮期,体力充沛;
对于情绪,有 ,处于低潮期,心情烦躁;
对于智力,有 ,处于高潮期,思维敏捷;
故今日同学甲体力充沛,心情烦躁,思维敏捷.
故答案为:A
【分析】 根据题意,由图象分析体力、情绪、智力的周期,由此分析同学甲的状态,即可得答案.
3.【答案】B
【解析】【解答】设y与时间t的函数关系式为,由题意可得,初始位置为,即初相为,故可得,,则,.
又函数周期是60(秒)且秒针按顺时针方向旋转,即,
所以,即,
.
令,则,解得.
故答案为:B
【分析】首先确定函数的周期,设y与时间t的函数关系式为,利用待定系数可求出函数的解析式,进而可求出 时t的取值范围.
4.【答案】C
【解析】【解答】当时,,则在上单调递增.设花开 花谢的时间分别为.
由,得,解得时;
由,得,解得时.
故在6时时中,观花的最佳时段约为8.7时时.
故答案为:C
【分析】先确定在上单调递增.设花开 花谢的时间分别为,再由,求得,.
5.【答案】D
【解析】【解答】因为当时,小球处于平衡位置,并开始向下移动,故,即,又,故,故,故当时,
故答案为:D
【分析】根据当时,小球处于平衡位置,并开始向下移动可求得,进而求得h的解析式,再代入求解即可.
6.【答案】C
【解析】【解答】如图,,
设表高,则由题知,,
所以,
因为,,,
所以,解得,
所以,表高(即的长)约为9.45米.
故答案为:C
【分析】利用已知条件结合正切函数的定义,再结合作差法,进而得出表高。
7.【答案】B
【解析】【解答】因为,,
所以,
所以为等腰三角形,
所以米,
在中,,
所以米.
故答案为:B.
【分析】利用已知条件结合等腰三角形的定义和直角三角形中角的关系式,从而结合余弦函数的定义,进而得出岳阳楼的高度CD的长。
8.【答案】B
【解析】【解答】解:根据题意设,,
因为某摩天轮最高点距离地面高度为,转盘直径为,
所以,该摩天轮最低点距离地面高度为,
所以,解得,
因为开启后按逆时针方向匀速旋转,旋转一周需要,
所以,,解得,
因为时,,故,即,解得.
所以,
故答案为:B
【分析】根据题意,设,进而结合题意求解即可.
9.【答案】C
【解析】【解答】由于抵消噪声,所以振幅没有改变,周期没有改变,即,,
即,要想抵消噪声,需要主动降噪芯片生成的声波曲线是,
即,
因为,所以令,即,
故答案为:C
【分析】 根据题意可得通过主动降噪芯片生成的声波曲线是,从而可求φ的值.
10.【答案】D
【解析】【解答】由图像可知:8~13时这段时间温度先下降再升高,A不符合题意;
8~16时最大温度℃,最小温度℃,最大温差为℃,B不符合题意;
8~16时0℃以下的时长超过3小时,C不符合题意;
T=4×(13 11)=8=2πω,ω=π4,又过点(13,22),故22cos(π4 13+φ)=22,解得φ=3π4,
故f(x)=22cos(π4x+3π4),f(16)=22cos(π4 16+3π4)= 2,故16时温度为 2℃,D符合题意.
故答案为:D.
【分析】由图像直接判断A、B、C选项,求出解析式判断D选项即可.
11.【答案】D
【解析】【解答】解:函数 ,其图象与直线 相邻两个交点的距离为 ,
故函数的周期为 ,故 ,
若 对 恒成立,即当 时, 恒成立,
所以 ,解得
因为 ,所以 .
故答案为:D.
【分析】由题意可得函数的周期为 ,求得 .再根据当 时 恒成立,即 ,再结合 求得 的取值范围.
12.【答案】B
【解析】【解答】解:因为M是函数图像的一个最高点,K,N是函数图象上与它距离最近的两个对称中心,
又因为是边长为1的正三角形,
所以正三角形的高是点 的纵坐标,即,
所以,,即,
又因为,所以,
因为,所以.故.
因为函数为偶函数,所以,,
所以当时,最小为.
故答案为:B.
【分析】根据题意结合周期的公式即可求出的值,再由特殊点法代入计算出,由此即可得出函数的解析式,再结合正弦函数的图象和性质,正弦函数的周期公式以及单调性结合整体思想即可得出结果,然后对k赋值计算出结果即可。
13.【答案】C
【解析】【解答】令和相等可得,即;
此时,即等腰直角三角形的斜边上的高为,所以底边长为,
令底边的一个端点为,则另一个端点为,
所以,即,
当时,的最小值,最小值为
故答案为:C.
【分析】先根据函数值相等求出,可得,由此可知等腰直角三角形的斜边上的高为,所以底边长为,令底边的一个端点为,则另一个端点为,由此可知,可得,据此即可求出结果.
14.【答案】B
【解析】【解答】因函数最大值为110,最小值为10,因此有,解得,
而函数的周期为10,即,则,
又当时,,则,而,解得,
所以。
故答案为:B
【分析】利用已知条件结合正弦型函数的最值求解方法,进而得出A,B的值,再利用正弦型函数的最小正周期公式得出的值,再结合五点对应法和,进而得出的值,从而得出 (米)关于(分钟)的解析式 。
15.【答案】B
【解析】【解答】由图1可得,又,
所以,所以,
所以,
该地的纬度约为北纬。
故答案为:B.
【分析】利用已知条件结合正切函数的定义和角之间的关系,进而得出该地的纬度约为北纬的度数。
16.【答案】D
【解析】【解答】解:由题意,因为()过点,
所以,
所以,所以,即,
又,所以,所以,
所以当时,,所以,
点N的纵坐标为,
故答案为:D.
【分析】将点代入方程,求出,然后利用已知条件求出,从而将代入方程即可求解.
17.【答案】B
【解析】【解答】由可知,
当时,,
当时,,
若在,时刻,游客距离地面的高度相等,
则由对称性可知此时的最小值为.
故答案为:B.
【分析】由结合余弦型函数的图象求最值的方法得出h的最小值,若在,时刻,游客距离地面的高度相等,则由对称性可知此时的最小值。
18.【答案】D
【解析】【解答】如图所示,
地球表面某地正午太阳高度角为,为此时太阳直射点纬度,为当地纬度值,那么这三个量满足,
当且为正值,可得,即,
设木杆的影长为,可得,
因为甲、乙、丙、丁四个小组在同一场地进行,得到影长分别为,
所以当时,取得最小值,此时求得最大值,
所以四组中对通州区当地纬度估测值最大的一组是丁组.
故答案为:D.
【分析】利用已知条件结合正切函数的定义和正切函数的图象求角的最值的方法,进而得出四组中对通州区当地纬度估测值最大的一组。
19.【答案】C
【解析】【解答】设点P距离地面高度h与时间t的函数解析式为,
由题意,得,,,
所以,
又因为,所以,
所以,
令,即,
故,即在摩天轮转动的一圈内,
有分钟会有这种最佳视觉效果。
故答案为:C.
【分析】利用已知条件求出函数的解析式为,令,从而解不等式组求出t的取值范围,进而得出在摩天轮转动的一圈内具有最佳视觉效果的时间长度。
20.【答案】A
【解析】【解答】因为,,
所以,,
,即,,
,即,,
则,
因为,所以,,
因为,所以的最大值为9。
故答案为:A.
【分析】利用已知条件结合作差法和代入法得出和,进而得出,再利用得出,再结合,进而得出的最大值。
21.【答案】(1)解:由已知可得,
∵盛水筒运动的角速度,
∴秒后盛水筒转过的角度为,
此时可得以为终边的角
∴
(2)解:当第一筒水到达最高位置时,是第一次取得最大值,此时,得(秒),
相邻两个盛水筒倾倒的时间差为(秒),
(3)解:完成该稻田的浇灌需倾倒筒水,
所需时间为秒,约为13.9小时.
所以第一筒水倾倒的时刻为20秒,相邻两个盛水筒倾倒的时间差为5秒,约13.9小时可完成该稻田的浇灌.
【解析】【分析】(1)根据题意结合任意角三角函数的定义分析求解;
(2)结合三角函数的周期运算求解;
(3)根据题意运算求解即可.
22.【答案】(1)解:依题意,, ,即,则,
由给定的图形知,,又,即有,
所以与的函数解析式是;
(2)解:令,即
所以,解得,
所以水车在一个旋转周期内,盛水筒在水面以上的时长为.
【解析】【分析】(1)结合图形,可确定 与的函数解析式;
(2) 令 ,利用正弦函数的性质可求出t的范围,进而得盛水筒在水面以上的时长.
23.【答案】(1)解:设座舱与地面的距离与时间的函数关系的解析式为
,,,,则,,
,依题意,,
当时,,,
取,,
,当时,1号舱与地面的距离为;
(2)解:依题意,,
,
令,,解得,,
当,时,取得最大值,故,
即,即的取值范围是.
【解析】【分析】(1) 设座舱与地面的距离与时间的函数关系的解析式为,,,,根据所给条件,求出A,b,,,即可得到函数解析式,再令t=6代入计算求出 1号座舱与地面的距离;
(2)依题意可得h1 , h5 ,从而得到高度差函数 ,利用两角和差的正弦公式化简,再结合正弦函数的性质求出函数取得最大值时t的值,即可求解出 的取值范围.
24.【答案】(1)解:如图,过O作交PB于点C,设筒车与水面的交点为M,N,连接OM.
因为筒车转一周需要1分钟,所以筒车每秒钟转,则.
又因为,,所以,
则.
,,
即,.
(2)解:不妨设,由题意得,
故,
①,,解得,,故,当且仅当,时,等号成立,
②,,解得,显然当时,取得最小值,最小值为.
综上,的最小值为40.
【解析】【分析】 (1)过O作交PB于点C,设筒车与水面的交点为M,N,连接OM,根据已知条件易知,又因为,,得,根据即可求得函数的解析式;
(2) 不妨设,由题意得, 即分两种情况讨论,计算即可.
25.【答案】(1)解:设,
根据函数的物理意义可知:
,
由题意可知当时,,
则,所以,
则,
又因为函数的最小正周期为,
所以,
所以;
(2)解:根据题意可知,,
即,
当水轮转动一圈时,,,
可得:,
所以此时,
解得,
又因为 (秒,
即水轮转动任意一圈内,有秒的时间点距水面的高度不低于2米.
【解析】【分析】(1)首先设出函数的解析式,然后结合题意和物理意义及待定系数法确定参数值即可求得函数的解析式;
(2)结合(1)中函数的解析式求解三角不等式即可确定有多长时间点P距离水面的高度不低于2米.
26.【答案】(1)解:根据图象,,,
∵,∴,
由当,,解得.
(2)解:由(1)得,,
∵,则,由,即,得.
故.
∴适宜开空调的时间段为
【解析】【分析】(1)利用已知条件结合余弦型函数的部分图象,再结合函数的最高点的纵坐标和对称轴的位置,进而得出 A,b的值,再结合余弦型函数的最小正周期公式得出的值,再利用五点对应法和的取值范围,进而得出的值。
(2)利用(1)求出函数的解析式,再利用余弦型函数的图象额已知条件,进而得出适宜开空调的时间段。
27.【答案】(1)解:如图设座舱距离地面最近的位置为点P,以轴心为原点,与地面平行的直线为轴建立直角坐标系.
设时,游客上座舱时位于点,
根据摩天轮转一周大约需要24min,可知座舱转动的角速度约为,由题意可得
,.
(2)解:时,满足题意.
解得,,
令,解得
又因为,故,则.
所以
游客在摩天轮转动一周过程中可观赏到全园景色的时间为8分钟.
【解析】【分析】 (1)设座舱距离地面最近的位置为点P,以轴心为原点,与地面平行的直线为轴建立直角坐标系,设时,游客上座舱时位于点,根据摩天轮转一周大约需要24min,可知座舱转动的角速度,由题意可得在转动一周的过程中,H关于的函数解析式。
(2)利用已知条件得出时,进而得出,再结合正弦型函数的图象和,进而得出t的取值范围,从而得出游客在摩天轮转动一周过程中可观赏到全园景色的时间。
28.【答案】(1)解:因为小球振动过程中最高点与最低点的距离为,所以.
因为在一次振动中,小球从最高点运动至最低点所用时间为,所以周期为2,
即,所以.
所以,.
(2)解:由题意,当时,小球第一次到达最高点,
以后每隔一个周期都出现一次最高点,
因为小球在内经过最高点的次数恰为50次,
所以.
因为,所以,
所以的取值范围为.
(注:的取值范围不考虑开闭)
【解析】【分析】(1)首先根据题意得到,,从而得到 ,;
(2)根据题意,当时,小球第一次到达最高点,从而得到,再根据周期为2,即可得到.
29.【答案】(1)由题意设 ,则 , ,则 ,
由题意 , 是锐角,所以 ,
, , ,
所以 ;
(2)河水上涨 米,在 中, , .
(3)水车转速加快到原来的2倍,则周期变为原来的一半,即 , ,
所以 .
【解析】【分析】(1)利用已知条件结合正弦型函数的最高点的纵坐标求出A的值,再利用正弦型函数的最小正周期公式求出的值,再利用特殊点法,进而结合的取值范围,从而求出的值,进而求出正弦型函数f(t)的解析式。
(2)利用已知条件结合正弦函数的定义,进而求出 ∠QON的大小。
(3)利用水车转速加快到原来的2倍,则周期变为原来的一半,从而求出正弦型函数的最小正周期,再利用正弦型函数的最小正周期公式,进而求出的值,进而求出函数f(t)的解析式。
30.【答案】(1)解:依题意,函数定义域是R,
,
即,成立,
所以函数是R上的周期为1的2级递减周期函数.
(2)解:因,是上的P级周期函数,则,即,
而当时,,当时,,,
当时,,则,
当时,,则,
……
当时,,则,
并且有:当时,,当时,,当时,,……,
当时,,
因是上的严格增函数,则有,解得,
所以当时,,且.
(3)解:假定存在非零实数k,使函数是R上的周期为T的T级周期函数,
即,恒有成立,则,恒有成立,
即,恒有成立,当时,,则,,
于是得,,要使恒成立,则有,
当,即时,由函数与的图象存在交点知,方程有解,
此时恒成立,则,即,
当,即时,由函数与的图象没有交点知,方程无解,
所以存在,符合题意,其中满足.
【解析】【分析】(1) 根据题意,化简,进而得到是R上的周期为1的2级递减周期函数;
(2) 根据题意得到,根据三角函数的性质,分类讨论,即可求得数的解析式,并求实数P的取值范围;
(3) 根据题意转化为,恒有成立,要使恒成立,得到,分和,两种情况讨论,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
