2023-2024学年人教版九年级数学上册24.1.3 弧、弦、圆心角 课件(共19张PPT)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册24.1.3 弧、弦、圆心角 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 751.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 13:17:06 | ||
图片预览




文档简介
(共19张PPT)
第二十四章 圆
九年级上册
人教版
学习一刻
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
第二十四章 圆
九年级上册
创作者:学习一刻
学习目标
1、理解圆的旋转不变性和中心对称性。
2、掌握圆心角的概念以及弧、弦、圆心角之间的等量关系;(重点)
3、能运用弧、弦、圆心角之间的相等关系解决有关的证明、计算问题.(难点)
知识回顾
1、圆既是_____对称图形,又是________对称图形,任何一条 所在的直线都是它的对称轴,对称中心是_______.
轴
中心
经过圆心
圆心
2、回顾什么是垂径定理及推论?
垂径定理:垂直与弦的直径平分这条弦,并 且平分这条弦所对的两段弧。
推论:平分弦(不是直径)的直径垂直与这条弦,并且平分这条弦所对的两段弧 。
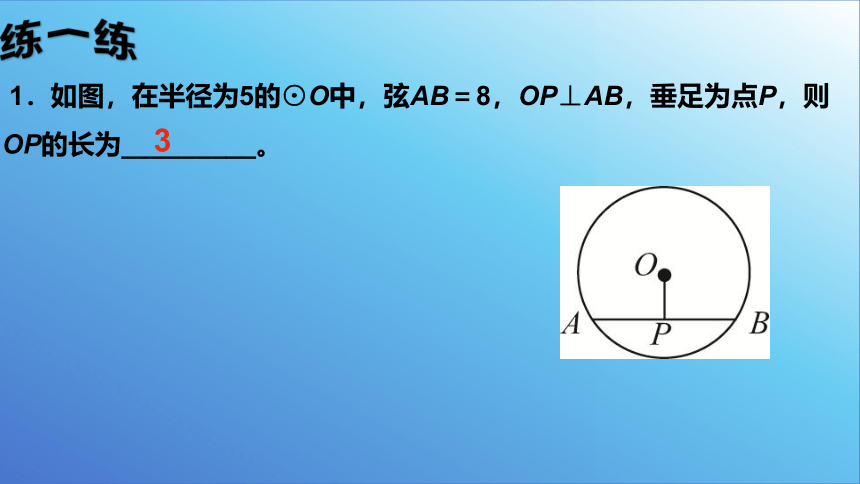
练一练
1.如图,在半径为5的⊙O中,弦AB=8,OP⊥AB,垂足为点P,则OP的长为_________。
3
知识点一 : 圆具有旋转不变性
圆具有旋转不变的特性,即一个圆绕着它的 旋转任意一个角度,都能与原来的图形 .
圆心
重合
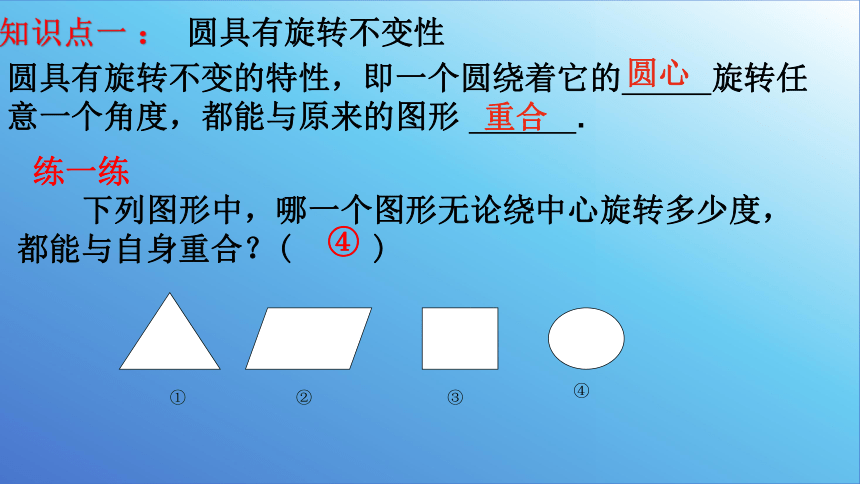
练一练
下列图形中,哪一个图形无论绕中心旋转多少度,都能与自身重合?( )
①
②
③
④
④
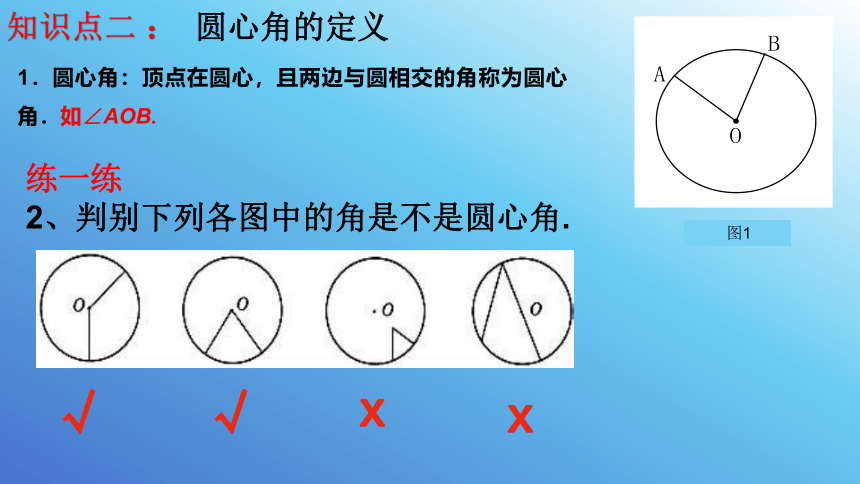
知识点二 : 圆心角的定义
图1
练一练
2、判别下列各图中的角是不是圆心角.
√
√
x
x
1.圆心角:顶点在圆心,且两边与圆相交的角称为圆心角.如∠AOB.
知识点三:
弧、弦、圆心角的关系
1、在⊙O中,把∠AOB连同 绕圆心 O旋转,使OA与OA'重合.那么它们所对的 和 、所对的弦AB和A B 有什么关系?
动手讨论
知识点三:
弧、弦、圆心角的关系
归纳:
1、在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦也 .
几何语言:
(1)∵∠1=∠2,
∴AB=A′B′, = ;
相等
相等
知识点三:
弧、弦、圆心角的关系
归纳:
2、在同圆或等圆中,如果两条弧相等,那么它们所对 的相等,所对的弦也 .
几何语言:
(2)∵AB=A′B′,
∴∠1=∠2, = ;
圆心角
相等
知识点三:
弧、弦、圆心角的关系
3、在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 ,所对的 也相等。
几何语言:
(3)∵ = ,
∴∠1=∠2,AB=A′B′.
相等
弧
知识点三:
弧、弦、圆心角的关系
温馨提示:同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也 .
相等
讲
题
例
∴AB=AC,
∵∠ACB=60°,
∴△ABC为等边三角形,
∴AB=BC=AC,
∴∠AOB=∠BOC=∠AOC.
练
练
一
50°
﹤
练
练
一
3.如图,在⊙O中,若点C是 的中点,∠A=40°,则∠BOC=______.
50°
4.如图,AB是⊙O的直径,AC,CD,DE,EF,FB都是⊙O的弦,且AC=CD=DE=EF=FB,则∠AOC=____________.
36°
练
练
一
51°
练
练
一
7.如图,点A,B是⊙O上的两点,∠AOB=120°,点C是 的中点.求证:四边形AOBC是菱形.
证明:如答图,连接OC,
∵点C是 的中点,
∠AOB=120°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
练
练
一
9.如图,已知C,D是以AB为直径的⊙O上的两点,连接BC,OC,OD,若OD∥BC,求证:D为 的中点.
证明:∵OB=OC,
∴∠B=∠C,
∵OD∥BC,
∴∠AOD=∠B,∠COD=∠C,
∴∠AOD=∠COD,
本部分内容讲解结束
按ESC键退出全屏播放
谢谢观赏!
第二十四章 圆
九年级上册
人教版
学习一刻
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
第二十四章 圆
九年级上册
创作者:学习一刻
学习目标
1、理解圆的旋转不变性和中心对称性。
2、掌握圆心角的概念以及弧、弦、圆心角之间的等量关系;(重点)
3、能运用弧、弦、圆心角之间的相等关系解决有关的证明、计算问题.(难点)
知识回顾
1、圆既是_____对称图形,又是________对称图形,任何一条 所在的直线都是它的对称轴,对称中心是_______.
轴
中心
经过圆心
圆心
2、回顾什么是垂径定理及推论?
垂径定理:垂直与弦的直径平分这条弦,并 且平分这条弦所对的两段弧。
推论:平分弦(不是直径)的直径垂直与这条弦,并且平分这条弦所对的两段弧 。
练一练
1.如图,在半径为5的⊙O中,弦AB=8,OP⊥AB,垂足为点P,则OP的长为_________。
3
知识点一 : 圆具有旋转不变性
圆具有旋转不变的特性,即一个圆绕着它的 旋转任意一个角度,都能与原来的图形 .
圆心
重合
练一练
下列图形中,哪一个图形无论绕中心旋转多少度,都能与自身重合?( )
①
②
③
④
④
知识点二 : 圆心角的定义
图1
练一练
2、判别下列各图中的角是不是圆心角.
√
√
x
x
1.圆心角:顶点在圆心,且两边与圆相交的角称为圆心角.如∠AOB.
知识点三:
弧、弦、圆心角的关系
1、在⊙O中,把∠AOB连同 绕圆心 O旋转,使OA与OA'重合.那么它们所对的 和 、所对的弦AB和A B 有什么关系?
动手讨论
知识点三:
弧、弦、圆心角的关系
归纳:
1、在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦也 .
几何语言:
(1)∵∠1=∠2,
∴AB=A′B′, = ;
相等
相等
知识点三:
弧、弦、圆心角的关系
归纳:
2、在同圆或等圆中,如果两条弧相等,那么它们所对 的相等,所对的弦也 .
几何语言:
(2)∵AB=A′B′,
∴∠1=∠2, = ;
圆心角
相等
知识点三:
弧、弦、圆心角的关系
3、在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 ,所对的 也相等。
几何语言:
(3)∵ = ,
∴∠1=∠2,AB=A′B′.
相等
弧
知识点三:
弧、弦、圆心角的关系
温馨提示:同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也 .
相等
讲
题
例
∴AB=AC,
∵∠ACB=60°,
∴△ABC为等边三角形,
∴AB=BC=AC,
∴∠AOB=∠BOC=∠AOC.
练
练
一
50°
﹤
练
练
一
3.如图,在⊙O中,若点C是 的中点,∠A=40°,则∠BOC=______.
50°
4.如图,AB是⊙O的直径,AC,CD,DE,EF,FB都是⊙O的弦,且AC=CD=DE=EF=FB,则∠AOC=____________.
36°
练
练
一
51°
练
练
一
7.如图,点A,B是⊙O上的两点,∠AOB=120°,点C是 的中点.求证:四边形AOBC是菱形.
证明:如答图,连接OC,
∵点C是 的中点,
∠AOB=120°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
练
练
一
9.如图,已知C,D是以AB为直径的⊙O上的两点,连接BC,OC,OD,若OD∥BC,求证:D为 的中点.
证明:∵OB=OC,
∴∠B=∠C,
∵OD∥BC,
∴∠AOD=∠B,∠COD=∠C,
∴∠AOD=∠COD,
本部分内容讲解结束
按ESC键退出全屏播放
谢谢观赏!
同课章节目录
