2023年广东省湛江市坡头区中考数学三模试卷(含解析)
文档属性
| 名称 | 2023年广东省湛江市坡头区中考数学三模试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 13:18:34 | ||
图片预览



文档简介
2023学年第二学期九年级调研测试
数学(问卷)
满分120分,考试用时120分钟.
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(3分)在,,0,﹣2这四个数中,为无理数的是( )
A. B. C.0 D.﹣2
2.(3分)2022年第11期某市小汽车增量调控竞价结束,个人车牌平均成交价约为86000元.86000用科学记数法表示应为( )
A.86×103 B.8.6×104 C.8.6×105 D.0.86×105
3.(3分)下列图形是轴对称图形而不是中心对称图形的是( )
A. B.
C. D.
4.(3分)下列计算正确的是( )
A.3x2﹣x2=3 B.﹣3a2﹣2a2=﹣a2
C.﹣2(x+1)=﹣2x﹣2 D.3(a﹣1)=3a﹣1
5.(3分)已知一组数据12、4、8、m、10,它们的平均数是8,则这一组数据的中位数为( )
A.4 B.8 C.10 D.12
6.(3分)某高校计划派出甲、乙、丙3名男生和A、B、C3名女生共6名志愿者参与北京冬奥会工作,现在将他们分配到北京、延庆2个赛区进行培训,其中1名男性志愿者和1名女性志愿者去北京赛区,其他都去延庆赛区,则甲和A恰好被选去北京赛区培训的概率为( )
A. B. C. D.
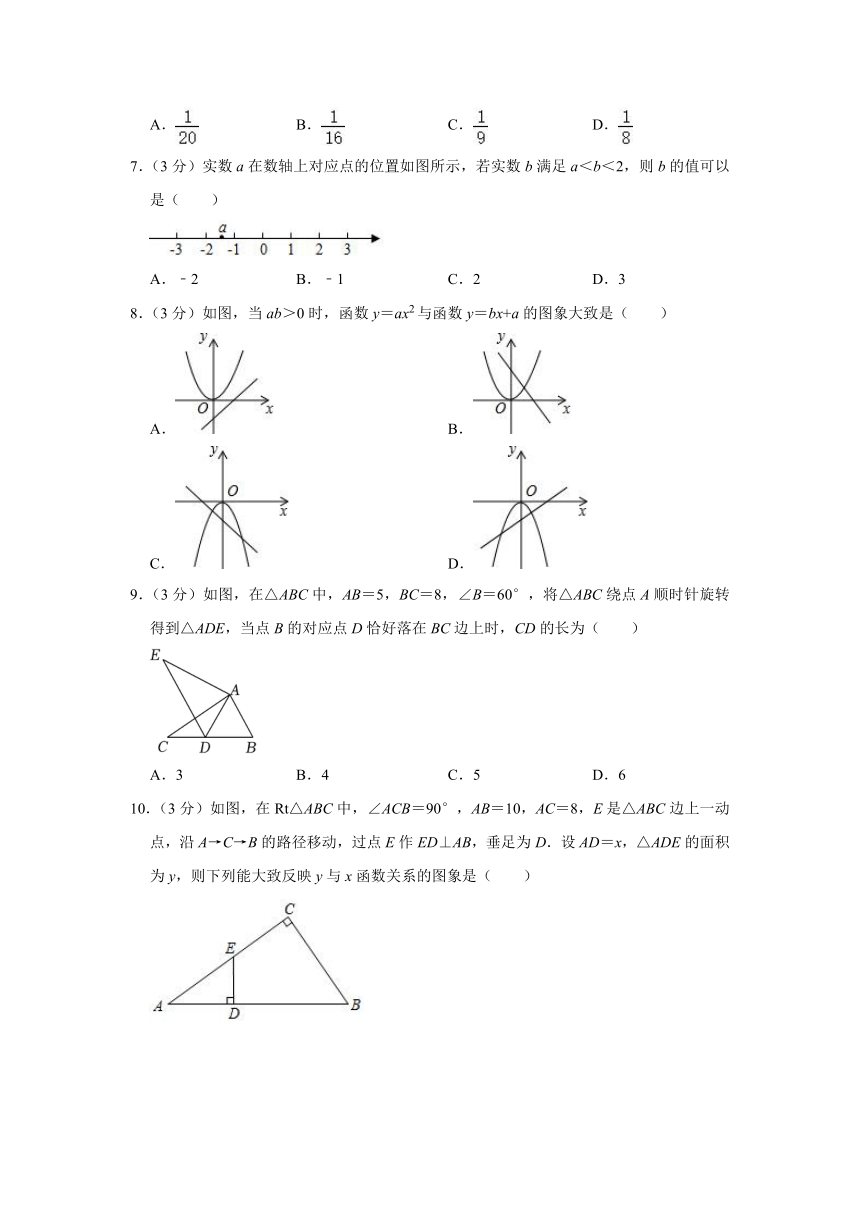
7.(3分)实数a在数轴上对应点的位置如图所示,若实数b满足a<b<2,则b的值可以是( )
A.﹣2 B.﹣1 C.2 D.3
8.(3分)如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A. B.
C. D.
9.(3分)如图,在△ABC中,AB=5,BC=8,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,CD的长为( )
A.3 B.4 C.5 D.6
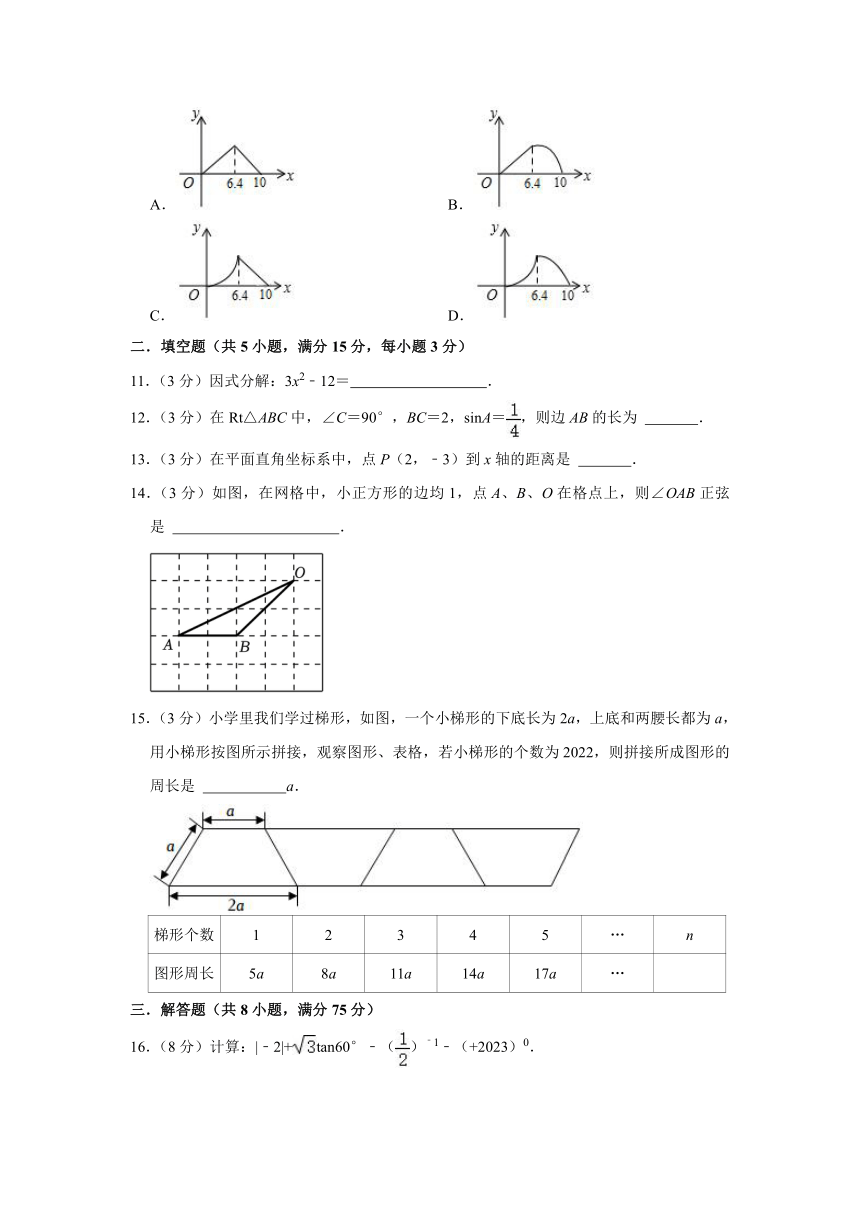
10.(3分)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E是△ABC边上一动点,沿A→C→B的路径移动,过点E作ED⊥AB,垂足为D.设AD=x,△ADE的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. B.
C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)因式分解:3x2﹣12= .
12.(3分)在Rt△ABC中,∠C=90°,BC=2,sinA=,则边AB的长为 .
13.(3分)在平面直角坐标系中,点P(2,﹣3)到x轴的距离是 .
14.(3分)如图,在网格中,小正方形的边均1,点A、B、O在格点上,则∠OAB正弦是 .
15.(3分)小学里我们学过梯形,如图,一个小梯形的下底长为2a,上底和两腰长都为a,用小梯形按图所示拼接,观察图形、表格,若小梯形的个数为2022,则拼接所成图形的周长是 a.
梯形个数 1 2 3 4 5 … n
图形周长 5a 8a 11a 14a 17a …
三.解答题(共8小题,满分75分)
16.(8分)计算:|﹣2|+tan60°﹣()﹣1﹣(+2023)0.
17.(8分)先化简再求值:(1﹣)÷,其中x=3.
18.(8分)某学校八、九年级各有学生200人,为了提高学生的身体素质,学校开展了主题为“快乐运动,健康成长”的系列体育健身活动.为了了解学生的运动状况,从八、九年级各随机抽取40名学生进行了体能测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
a.八年级学生成绩的频数分布直方图如下(数据分为五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100)
b.八年级学生成绩在70≤x<80这一组的是:
70 71 73 73 73 74 76 77 78 79
c.九年级学生成绩的平均数、中位数、众数、优秀率如下:
平均数 中位数 众数 优秀率
79 76 84 40%
根据以上信息,回答下列问题:
(1)在此次测试中,小腾的成绩是74分,在年级排名是第17名,由此可知他是 年级的学生(填“八”,或“九”);
(2)根据上述信息,推断 年级学生运动状况更好,理由为 ;(至少从两个不同的角度说明推断的合理性)
(3)假设八年级全体学生都参加了此次测试,如果年级排名在前70名的学生可以被评选为“运动达人”,预估八年级学生至少要达到多少分才可以入选.
19.(9分)如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=12,MN=4,求菱形BNDM的周长.
20.(9分)京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
21.(9分)如图所示,直线AB与反比例函数的图象相交于A,B两点,已知A(1,4).
(1)求反比例函数的解析式;
(2)直线AB交x轴于点C,连接OA,当△AOC的面积为6时,求直线AB的解析式.
22.(12分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
23.(12分)已知抛物线y=x2+c与x轴交于A(﹣1,0),B两点,交y轴于点C.
(1)求抛物线的解析式;
(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG.求n的值并直接写出m的取值范围(利用图1完成你的探究).
(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1. 解:,0,﹣2是有理数,
是无理数,
故选:A.
2. 解:86000=8.6×104.
故选:B.
3. 解:A.既是轴对称图形,又是中心对称图形,故本选项不符合题意;
B.既是轴对称图形,又是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:C.
4. 解:A.3x2﹣x2=2x2,此选项计算错误;
B.﹣3a2﹣2a2=﹣5a2,此选项计算错误;
C.﹣2(x+1)=﹣2x﹣2,此选项计算正确;
D.3(a﹣1)=3a﹣3,此选项计算错误;
故选:C.
5. 解:由题意知=8,
解得m=6,
则这组数据为4、6、8、10、12,
所以这组数据的中位数为8,
故选:B.
6. 解:根据题意列表如下:
甲 乙 丙
A (甲,A) (乙,A) (丙,A)
B (甲,B) (乙,B) (丙,B)
C (甲,C) (乙,C) (丙,C)
一共有9种等可能的情况,其中甲和A恰好被选去北京赛区培训的有1种情况,
则甲和A恰好被选去北京赛区培训的概率为.
故选:C.
7. 解:∵1<a<2,
∴﹣2<﹣a<﹣1,
∵﹣a<b<a,
∴b只能是﹣1.
故选:B.
8. 解:A、根据一次函数得出a<0,b>0,根据二次函数得出a>0,则ab<0,故本选项错误;
B、根据一次函数得出a>0,b<0,根据二次函数得出a>0,则ab<0,故本选项错误;
C、根据一次函数得出a<0,b<0,根据二次函数得出a<0,则ab>0,故本选项正确;
D、根据一次函数得出a<0,b>0,根据二次函数得出a<0,则ab<0,故本选项错误;
故选:C.
9. 解:∵将△ABC绕点A按顺时针旋转一定角度得到△ADE,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形,
∴BD=AB,
∵AB=5,BC=8,
∴CD=BC﹣BD=8﹣5=3.
故选:A.
10. 解:在Rt△ABC中,∠ACB=90°,AB=10,AC=8,
由勾股定理可得BC=6,
根据点E的运动,需要分段讨论:
①当点E在AC上时,如图,
∵DE⊥AB,
∴∠ADE=∠C=90°,
∵∠A=∠A,
∴△ADE∽△ACB,
∴AD:DE:AE=AC:BC:AB=4:3:5,
∵AD=x,
∴AE=,DE=x;
此时0≤≤8,即0≤x≤6.4,
∴y= x x=x2;是开口向上的一段抛物线;排除A,B,
当点E在BC上时,6.4<x≤10,如图,
∵∠BDE=∠ACB=90°,∠B=∠B,
∴△BDE∽△BCA,
∴DE:BD:BE=AC:BC:AB=4:3:5,
∵AD=x,
∴BD=10﹣x,∴
∴DE=(10﹣x),
∴y= (10﹣x) x=﹣x2+x,开口向下的抛物线,
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
11. 解:原式=3(x2﹣4)
=3(x+2)(x﹣2).
故答案为:3(x+2)(x﹣2).
12. 解:Rt△ABC中,
∵sinA==,BC=2,
∴AB=2×4=8.
故答案为:8.
13. 解:点P(2,﹣3)到x轴的距离是|﹣3|=3,
故答案为:3.
14. 解:如图,过点O作OC⊥AB的延长线于点C,
则AC=4,OC=2,
在Rt△ACO中,AO===2,
∴sin∠OAB===.
故答案为:.
15. 解:∵1个梯形时,其周长5a=2a+3a,
2个梯形时,其周长8a=2a+2×3a,
3个梯形时,其周长11a=2a+3×3a,
…
∴n个梯形时,其周长为2a+3na=(2+3n)a,
∴2022个梯形时,其周长为:(2+3×2022)a=6068a.
故答案为:6068.
三.解答题(共8小题,满分75分)
16. 解:|﹣2|+tan60°﹣()﹣1﹣(+2023)0
=2+×﹣2﹣1
=2+3﹣2﹣1
=2.
17. 解:当x=3时,
原式=
=
=4
18. 解:(1)由题意得:八年级学生成绩位于第20位,第21位的是71、73,
∴八年级学生成绩的中位数为 分,
∵小腾的成绩是74分,在年级排名是第17名,可知其所在年级中位数应该不大于74,因此他应该在八年级;
(2)九年级学生运动状况更好,理由如下:
①九年级优秀率40%,八年级优秀率为=30%,说明九年级体能测试优秀人数更多;
②九年级中位数为76分,八年级为72分,说明九年级一半的同学测试成绩高于76分,而八年级一半同学的测试成绩仅高于72分;
(3)总体中“运动达人”占=35%,
∴样本中“运动达人”有40×35%=14人,
∵80≤x<90的有9人,而90≤x<100的有3人,
∴再从70≤x<80成绩中,从大到小找出第2个为78分,
∴八年级学生至少要达到78分才可以入选.
19. (1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:由(1)可知,OB=BD=6,OM=ON=MN=2,四边形BNDM是菱形,
∴BN=DN=DM=BM,
∵MN⊥BD,
∴∠BON=90°,
∴BN===2,
∴菱形BNDM的周长=4BN=8.
20. 解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要x天.根据题意,得 .
解得 x=90.
经检验,x=90是原方程的根.
∴x=×90=60.
答:甲、乙两队单独完成这项工程分别需60天和90天.
(2)设甲、乙两队合作完成这项工程需要y天,
则有 .
解得 y=36.
需要施工费用:36×(8.4+5.6)=504(万元).
∵504>500.
∴工程预算的施工费用不够用,需追加预算4万元.
21. 解:(1)由已知得反比例函数解析式为y=,
∵点A(1,4)在反比例函数的图象上,
∴4=,
∴k=4,
∴反比例函数的解析式为y=.
(2)设C的坐标为(﹣a,0)(a>0)
∵S△AOC=6,∴,
解得:a=3,
∴C(﹣3,0),
设直线AB的解析式为:y=kx+b
∵C(﹣3,0),A(1,4)在直线AB上,
∴,
解得:k=1,b=3,
∴直线AB的解析式为:y=x+3.
22. 证明:(1)如图,连接OD.
∵DE为切线,
∴∠EDC+∠ODC=90°;
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠EDC=∠ECD,
∴ED=EC;
∵AC为直径,
∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,
∴∠B=∠BDE,
∴ED=BE.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,
∴∠ADC=∠ACB=∠BDC=90°,
又∵∠B=∠B
∴△ABC∽△CDB,
∴,
∴BC2=BD BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;
∵AC为直径,
∴∠ADC=90°,
∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.
23. 解:(1)把A(﹣1,0)代入
得c=﹣,
∴抛物线解析式为
(2)如图1,过点C作CH⊥EF于点H,
∵∠CEF=∠CFG,FG⊥y轴于点G
∴△EHC∽△FGC
∵E(m,n)
∴F(m,)
又∵C(0,﹣)
∴EH=n+,CH=﹣m,FG=﹣m,CG=m2
又∵,
则
∴n+=2
∴n=
当F点位于E点上方时,则∠CEF>90°;又∠CFG肯定为锐角,故这种情形不符合题意.
由此当n=时,代入抛物线解析式,求得m=±2,
又E点位于第二象限,所以﹣2<m<0.
(3)由题意可知P(t,0),M(t,)
∵PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,
∴△OPM∽△QPB.
∴.
其中OP=t,PM=,PB=1﹣t,
∴PQ=.
BQ=
∴PQ+BQ+PB=.
∴△PBQ的周长为2.
数学(问卷)
满分120分,考试用时120分钟.
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(3分)在,,0,﹣2这四个数中,为无理数的是( )
A. B. C.0 D.﹣2
2.(3分)2022年第11期某市小汽车增量调控竞价结束,个人车牌平均成交价约为86000元.86000用科学记数法表示应为( )
A.86×103 B.8.6×104 C.8.6×105 D.0.86×105
3.(3分)下列图形是轴对称图形而不是中心对称图形的是( )
A. B.
C. D.
4.(3分)下列计算正确的是( )
A.3x2﹣x2=3 B.﹣3a2﹣2a2=﹣a2
C.﹣2(x+1)=﹣2x﹣2 D.3(a﹣1)=3a﹣1
5.(3分)已知一组数据12、4、8、m、10,它们的平均数是8,则这一组数据的中位数为( )
A.4 B.8 C.10 D.12
6.(3分)某高校计划派出甲、乙、丙3名男生和A、B、C3名女生共6名志愿者参与北京冬奥会工作,现在将他们分配到北京、延庆2个赛区进行培训,其中1名男性志愿者和1名女性志愿者去北京赛区,其他都去延庆赛区,则甲和A恰好被选去北京赛区培训的概率为( )
A. B. C. D.
7.(3分)实数a在数轴上对应点的位置如图所示,若实数b满足a<b<2,则b的值可以是( )
A.﹣2 B.﹣1 C.2 D.3
8.(3分)如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A. B.
C. D.
9.(3分)如图,在△ABC中,AB=5,BC=8,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,CD的长为( )
A.3 B.4 C.5 D.6
10.(3分)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E是△ABC边上一动点,沿A→C→B的路径移动,过点E作ED⊥AB,垂足为D.设AD=x,△ADE的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. B.
C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)因式分解:3x2﹣12= .
12.(3分)在Rt△ABC中,∠C=90°,BC=2,sinA=,则边AB的长为 .
13.(3分)在平面直角坐标系中,点P(2,﹣3)到x轴的距离是 .
14.(3分)如图,在网格中,小正方形的边均1,点A、B、O在格点上,则∠OAB正弦是 .
15.(3分)小学里我们学过梯形,如图,一个小梯形的下底长为2a,上底和两腰长都为a,用小梯形按图所示拼接,观察图形、表格,若小梯形的个数为2022,则拼接所成图形的周长是 a.
梯形个数 1 2 3 4 5 … n
图形周长 5a 8a 11a 14a 17a …
三.解答题(共8小题,满分75分)
16.(8分)计算:|﹣2|+tan60°﹣()﹣1﹣(+2023)0.
17.(8分)先化简再求值:(1﹣)÷,其中x=3.
18.(8分)某学校八、九年级各有学生200人,为了提高学生的身体素质,学校开展了主题为“快乐运动,健康成长”的系列体育健身活动.为了了解学生的运动状况,从八、九年级各随机抽取40名学生进行了体能测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
a.八年级学生成绩的频数分布直方图如下(数据分为五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100)
b.八年级学生成绩在70≤x<80这一组的是:
70 71 73 73 73 74 76 77 78 79
c.九年级学生成绩的平均数、中位数、众数、优秀率如下:
平均数 中位数 众数 优秀率
79 76 84 40%
根据以上信息,回答下列问题:
(1)在此次测试中,小腾的成绩是74分,在年级排名是第17名,由此可知他是 年级的学生(填“八”,或“九”);
(2)根据上述信息,推断 年级学生运动状况更好,理由为 ;(至少从两个不同的角度说明推断的合理性)
(3)假设八年级全体学生都参加了此次测试,如果年级排名在前70名的学生可以被评选为“运动达人”,预估八年级学生至少要达到多少分才可以入选.
19.(9分)如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=12,MN=4,求菱形BNDM的周长.
20.(9分)京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
21.(9分)如图所示,直线AB与反比例函数的图象相交于A,B两点,已知A(1,4).
(1)求反比例函数的解析式;
(2)直线AB交x轴于点C,连接OA,当△AOC的面积为6时,求直线AB的解析式.
22.(12分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
23.(12分)已知抛物线y=x2+c与x轴交于A(﹣1,0),B两点,交y轴于点C.
(1)求抛物线的解析式;
(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG.求n的值并直接写出m的取值范围(利用图1完成你的探究).
(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1. 解:,0,﹣2是有理数,
是无理数,
故选:A.
2. 解:86000=8.6×104.
故选:B.
3. 解:A.既是轴对称图形,又是中心对称图形,故本选项不符合题意;
B.既是轴对称图形,又是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:C.
4. 解:A.3x2﹣x2=2x2,此选项计算错误;
B.﹣3a2﹣2a2=﹣5a2,此选项计算错误;
C.﹣2(x+1)=﹣2x﹣2,此选项计算正确;
D.3(a﹣1)=3a﹣3,此选项计算错误;
故选:C.
5. 解:由题意知=8,
解得m=6,
则这组数据为4、6、8、10、12,
所以这组数据的中位数为8,
故选:B.
6. 解:根据题意列表如下:
甲 乙 丙
A (甲,A) (乙,A) (丙,A)
B (甲,B) (乙,B) (丙,B)
C (甲,C) (乙,C) (丙,C)
一共有9种等可能的情况,其中甲和A恰好被选去北京赛区培训的有1种情况,
则甲和A恰好被选去北京赛区培训的概率为.
故选:C.
7. 解:∵1<a<2,
∴﹣2<﹣a<﹣1,
∵﹣a<b<a,
∴b只能是﹣1.
故选:B.
8. 解:A、根据一次函数得出a<0,b>0,根据二次函数得出a>0,则ab<0,故本选项错误;
B、根据一次函数得出a>0,b<0,根据二次函数得出a>0,则ab<0,故本选项错误;
C、根据一次函数得出a<0,b<0,根据二次函数得出a<0,则ab>0,故本选项正确;
D、根据一次函数得出a<0,b>0,根据二次函数得出a<0,则ab<0,故本选项错误;
故选:C.
9. 解:∵将△ABC绕点A按顺时针旋转一定角度得到△ADE,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形,
∴BD=AB,
∵AB=5,BC=8,
∴CD=BC﹣BD=8﹣5=3.
故选:A.
10. 解:在Rt△ABC中,∠ACB=90°,AB=10,AC=8,
由勾股定理可得BC=6,
根据点E的运动,需要分段讨论:
①当点E在AC上时,如图,
∵DE⊥AB,
∴∠ADE=∠C=90°,
∵∠A=∠A,
∴△ADE∽△ACB,
∴AD:DE:AE=AC:BC:AB=4:3:5,
∵AD=x,
∴AE=,DE=x;
此时0≤≤8,即0≤x≤6.4,
∴y= x x=x2;是开口向上的一段抛物线;排除A,B,
当点E在BC上时,6.4<x≤10,如图,
∵∠BDE=∠ACB=90°,∠B=∠B,
∴△BDE∽△BCA,
∴DE:BD:BE=AC:BC:AB=4:3:5,
∵AD=x,
∴BD=10﹣x,∴
∴DE=(10﹣x),
∴y= (10﹣x) x=﹣x2+x,开口向下的抛物线,
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
11. 解:原式=3(x2﹣4)
=3(x+2)(x﹣2).
故答案为:3(x+2)(x﹣2).
12. 解:Rt△ABC中,
∵sinA==,BC=2,
∴AB=2×4=8.
故答案为:8.
13. 解:点P(2,﹣3)到x轴的距离是|﹣3|=3,
故答案为:3.
14. 解:如图,过点O作OC⊥AB的延长线于点C,
则AC=4,OC=2,
在Rt△ACO中,AO===2,
∴sin∠OAB===.
故答案为:.
15. 解:∵1个梯形时,其周长5a=2a+3a,
2个梯形时,其周长8a=2a+2×3a,
3个梯形时,其周长11a=2a+3×3a,
…
∴n个梯形时,其周长为2a+3na=(2+3n)a,
∴2022个梯形时,其周长为:(2+3×2022)a=6068a.
故答案为:6068.
三.解答题(共8小题,满分75分)
16. 解:|﹣2|+tan60°﹣()﹣1﹣(+2023)0
=2+×﹣2﹣1
=2+3﹣2﹣1
=2.
17. 解:当x=3时,
原式=
=
=4
18. 解:(1)由题意得:八年级学生成绩位于第20位,第21位的是71、73,
∴八年级学生成绩的中位数为 分,
∵小腾的成绩是74分,在年级排名是第17名,可知其所在年级中位数应该不大于74,因此他应该在八年级;
(2)九年级学生运动状况更好,理由如下:
①九年级优秀率40%,八年级优秀率为=30%,说明九年级体能测试优秀人数更多;
②九年级中位数为76分,八年级为72分,说明九年级一半的同学测试成绩高于76分,而八年级一半同学的测试成绩仅高于72分;
(3)总体中“运动达人”占=35%,
∴样本中“运动达人”有40×35%=14人,
∵80≤x<90的有9人,而90≤x<100的有3人,
∴再从70≤x<80成绩中,从大到小找出第2个为78分,
∴八年级学生至少要达到78分才可以入选.
19. (1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:由(1)可知,OB=BD=6,OM=ON=MN=2,四边形BNDM是菱形,
∴BN=DN=DM=BM,
∵MN⊥BD,
∴∠BON=90°,
∴BN===2,
∴菱形BNDM的周长=4BN=8.
20. 解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要x天.根据题意,得 .
解得 x=90.
经检验,x=90是原方程的根.
∴x=×90=60.
答:甲、乙两队单独完成这项工程分别需60天和90天.
(2)设甲、乙两队合作完成这项工程需要y天,
则有 .
解得 y=36.
需要施工费用:36×(8.4+5.6)=504(万元).
∵504>500.
∴工程预算的施工费用不够用,需追加预算4万元.
21. 解:(1)由已知得反比例函数解析式为y=,
∵点A(1,4)在反比例函数的图象上,
∴4=,
∴k=4,
∴反比例函数的解析式为y=.
(2)设C的坐标为(﹣a,0)(a>0)
∵S△AOC=6,∴,
解得:a=3,
∴C(﹣3,0),
设直线AB的解析式为:y=kx+b
∵C(﹣3,0),A(1,4)在直线AB上,
∴,
解得:k=1,b=3,
∴直线AB的解析式为:y=x+3.
22. 证明:(1)如图,连接OD.
∵DE为切线,
∴∠EDC+∠ODC=90°;
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠EDC=∠ECD,
∴ED=EC;
∵AC为直径,
∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,
∴∠B=∠BDE,
∴ED=BE.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,
∴∠ADC=∠ACB=∠BDC=90°,
又∵∠B=∠B
∴△ABC∽△CDB,
∴,
∴BC2=BD BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;
∵AC为直径,
∴∠ADC=90°,
∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.
23. 解:(1)把A(﹣1,0)代入
得c=﹣,
∴抛物线解析式为
(2)如图1,过点C作CH⊥EF于点H,
∵∠CEF=∠CFG,FG⊥y轴于点G
∴△EHC∽△FGC
∵E(m,n)
∴F(m,)
又∵C(0,﹣)
∴EH=n+,CH=﹣m,FG=﹣m,CG=m2
又∵,
则
∴n+=2
∴n=
当F点位于E点上方时,则∠CEF>90°;又∠CFG肯定为锐角,故这种情形不符合题意.
由此当n=时,代入抛物线解析式,求得m=±2,
又E点位于第二象限,所以﹣2<m<0.
(3)由题意可知P(t,0),M(t,)
∵PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,
∴△OPM∽△QPB.
∴.
其中OP=t,PM=,PB=1﹣t,
∴PQ=.
BQ=
∴PQ+BQ+PB=.
∴△PBQ的周长为2.
同课章节目录
