第23章 旋转 单元综合训练(无答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 第23章 旋转 单元综合训练(无答案)2023-2024学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 545.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 14:28:40 | ||
图片预览


文档简介
第23章 旋转 单元综合训练
一、单选题
1.一张薄纸,一双巧手,在一剪一刻间幻化出千姿百态的美丽图案,令人叹为观止,这就是剪纸艺术.剪纸作品形式多样,以下剪纸作品中既是轴对称图形又是中心对称图形的是( )
A. B. C.D.
2.如图所示,在方格纸中,三角形ABC经过变换得到三角形DEF,下列对变换过程叙述正确的是( )
A.把三角形ABC向左平移8格,再逆时针旋转90°
B.把三角形ABC绕点C逆时针旋转90°,再向左平移8格
C.把三角形ABC向左平移8格,再顺时针旋转90°
D.把三角形ABC绕点C顺时针旋转90°,再向左平移8格
3.如图,将△ABC绕点C顺时针旋转35°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠AFD的度数为( )
A.65° B.15° C.115° D.75°
4.在冬奥会开幕式上,美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案本身的设计呈现出充分的美感,它是一个中心对称图形.其实“雪花”图案也可以看成自身的一部分围绕图案的中心依次旋转一定角度得到的,这个角的度数可以是( )
A.30° B.45° C.60° D.90°
5.已知点与点关于原点对称,则的值为( )
A. B.5 C.3 D.
6.如图,RtABC中,∠A=90°,∠ABC=40°,将RtABC绕着点C逆时针旋转得RtEDC,且点E正好落在BC上,连接BD,则∠CBD的度数为( )
A.40° B.55° C.60° D.65°
7.如图,在中,,.将绕点O逆时针方向旋转90°,得到,连接.则线段的长为( )
A. B.2.5 C. D.
8.如图,在等腰中,,点D是的中点.将绕点A旋转后得到那么下列结论正确的是( )
A. B. C. D.
9.如图,在中,,,.点在上,且.连接,线段绕点顺时针旋转得到线段,连接,.则的面积是( )
A. B. C. D.
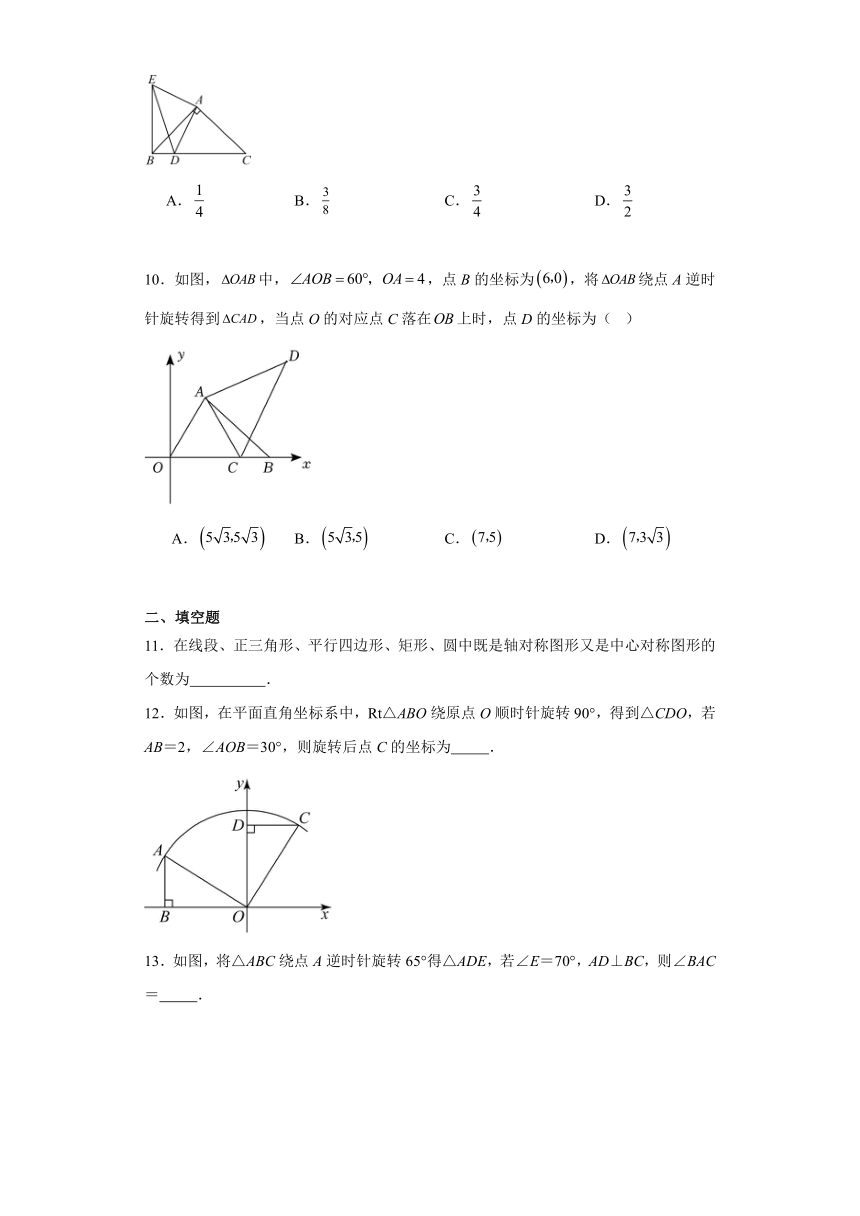
10.如图,中,,点B的坐标为,将绕点A逆时针旋转得到,当点O的对应点C落在上时,点D的坐标为( )
A. B. C. D.
二、填空题
11.在线段、正三角形、平行四边形、矩形、圆中既是轴对称图形又是中心对称图形的个数为 .
12.如图,在平面直角坐标系中,Rt△ABO绕原点O顺时针旋转90°,得到△CDO,若AB=2,∠AOB=30°,则旋转后点C的坐标为 .
13.如图,将△ABC绕点A逆时针旋转65°得△ADE,若∠E=70°,AD⊥BC,则∠BAC= .
14.如图,RtΔABC绕直角顶点C顺时针旋转90°,得到ΔDEC,连接AD,若∠BAC=25°,则∠ADE=
15.一副三角板按如图所示叠放在一起,其中点,重合,若固定,将绕着公共顶点,按逆时针方向旋转度,当旋转后的的一边与的某一边平行时,写出所有满足条件的的值 .
16.如图,在矩形中,,点M为边上的一个动点,线段绕点A逆时针旋转得到线段,连接,.当线段的长度最小时,的度数为 °.
三、解答题
17.如图,已知四边形和点P,画四边形,使四边形与四边形关于点P成中心对称.
18.如图,在中,,将绕点A顺时针方向旋转到的位置,连接,求的度数.
19.如图,与关于点中心对称,若点,分别在,上,且,求证:.
20.如图,在中,,将绕点B逆时针旋转到的延长线与相交于点F,连接,求证:.
21.图①②都是由边长为1的小等边三角形组成的正六边形,已经有5个小等边三角形涂上阴影,请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
(1)使得6个阴影小等边三角形组成的图形是轴对称图形,但不是中心对称图形.
(2)使得6个阴影小等边三角形组成的图形既是轴对称图形,又是中心对称图形.
22.如图所示,在边长为的小正方形组成的网格中.
(1)将沿轴正方向向上平移5个单位长度后,得到,请作出,并求出的长度;
(2)再将绕坐标原点顺时针旋转,得到,请作出,并直接写出点的坐标.
23.如图,四边形是菱形,边长为2,,点是射线上一动点(不与点重合),将线段绕点逆时针旋转得到线段,连接.
(1)如图1,当点恰好为中点时,直接写出线段与的数量关系为______________;
(2)当点不是中点时,如图2,(1)中的结论是否还成立?说明理由;
(3)连接,当时,请直接写出四边形的面积.
24.(探索发现)如图①,四边形是正方形,分别在边上,且,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法,如图①,将绕点A顺时针旋转,点与点重合,得到,连接.
(1)试判断之间的数量关系,并写出证明过程;
(2)如图①如果正方形的边长为4,求三角形的周长;
(3)如图②,点分别在正方形的边的延长线上,,连接,请写出之间的数量关系,并写出证明过程.
一、单选题
1.一张薄纸,一双巧手,在一剪一刻间幻化出千姿百态的美丽图案,令人叹为观止,这就是剪纸艺术.剪纸作品形式多样,以下剪纸作品中既是轴对称图形又是中心对称图形的是( )
A. B. C.D.
2.如图所示,在方格纸中,三角形ABC经过变换得到三角形DEF,下列对变换过程叙述正确的是( )
A.把三角形ABC向左平移8格,再逆时针旋转90°
B.把三角形ABC绕点C逆时针旋转90°,再向左平移8格
C.把三角形ABC向左平移8格,再顺时针旋转90°
D.把三角形ABC绕点C顺时针旋转90°,再向左平移8格
3.如图,将△ABC绕点C顺时针旋转35°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠AFD的度数为( )
A.65° B.15° C.115° D.75°
4.在冬奥会开幕式上,美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案本身的设计呈现出充分的美感,它是一个中心对称图形.其实“雪花”图案也可以看成自身的一部分围绕图案的中心依次旋转一定角度得到的,这个角的度数可以是( )
A.30° B.45° C.60° D.90°
5.已知点与点关于原点对称,则的值为( )
A. B.5 C.3 D.
6.如图,RtABC中,∠A=90°,∠ABC=40°,将RtABC绕着点C逆时针旋转得RtEDC,且点E正好落在BC上,连接BD,则∠CBD的度数为( )
A.40° B.55° C.60° D.65°
7.如图,在中,,.将绕点O逆时针方向旋转90°,得到,连接.则线段的长为( )
A. B.2.5 C. D.
8.如图,在等腰中,,点D是的中点.将绕点A旋转后得到那么下列结论正确的是( )
A. B. C. D.
9.如图,在中,,,.点在上,且.连接,线段绕点顺时针旋转得到线段,连接,.则的面积是( )
A. B. C. D.
10.如图,中,,点B的坐标为,将绕点A逆时针旋转得到,当点O的对应点C落在上时,点D的坐标为( )
A. B. C. D.
二、填空题
11.在线段、正三角形、平行四边形、矩形、圆中既是轴对称图形又是中心对称图形的个数为 .
12.如图,在平面直角坐标系中,Rt△ABO绕原点O顺时针旋转90°,得到△CDO,若AB=2,∠AOB=30°,则旋转后点C的坐标为 .
13.如图,将△ABC绕点A逆时针旋转65°得△ADE,若∠E=70°,AD⊥BC,则∠BAC= .
14.如图,RtΔABC绕直角顶点C顺时针旋转90°,得到ΔDEC,连接AD,若∠BAC=25°,则∠ADE=
15.一副三角板按如图所示叠放在一起,其中点,重合,若固定,将绕着公共顶点,按逆时针方向旋转度,当旋转后的的一边与的某一边平行时,写出所有满足条件的的值 .
16.如图,在矩形中,,点M为边上的一个动点,线段绕点A逆时针旋转得到线段,连接,.当线段的长度最小时,的度数为 °.
三、解答题
17.如图,已知四边形和点P,画四边形,使四边形与四边形关于点P成中心对称.
18.如图,在中,,将绕点A顺时针方向旋转到的位置,连接,求的度数.
19.如图,与关于点中心对称,若点,分别在,上,且,求证:.
20.如图,在中,,将绕点B逆时针旋转到的延长线与相交于点F,连接,求证:.
21.图①②都是由边长为1的小等边三角形组成的正六边形,已经有5个小等边三角形涂上阴影,请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
(1)使得6个阴影小等边三角形组成的图形是轴对称图形,但不是中心对称图形.
(2)使得6个阴影小等边三角形组成的图形既是轴对称图形,又是中心对称图形.
22.如图所示,在边长为的小正方形组成的网格中.
(1)将沿轴正方向向上平移5个单位长度后,得到,请作出,并求出的长度;
(2)再将绕坐标原点顺时针旋转,得到,请作出,并直接写出点的坐标.
23.如图,四边形是菱形,边长为2,,点是射线上一动点(不与点重合),将线段绕点逆时针旋转得到线段,连接.
(1)如图1,当点恰好为中点时,直接写出线段与的数量关系为______________;
(2)当点不是中点时,如图2,(1)中的结论是否还成立?说明理由;
(3)连接,当时,请直接写出四边形的面积.
24.(探索发现)如图①,四边形是正方形,分别在边上,且,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法,如图①,将绕点A顺时针旋转,点与点重合,得到,连接.
(1)试判断之间的数量关系,并写出证明过程;
(2)如图①如果正方形的边长为4,求三角形的周长;
(3)如图②,点分别在正方形的边的延长线上,,连接,请写出之间的数量关系,并写出证明过程.
同课章节目录
