圆周角(一)(四川省泸州市古蔺县)
图片预览



文档简介
课件9张PPT。7.5 圆周角2、引入圆周角:
如果顶点不在圆心而在圆上,则得到如左图的新的角∠ACB,它就是圆周角。(如左图)(演示图形,提出圆周角的定义)
定义:顶点在圆周上,并且两边都和圆相
交的角叫做圆周角.
3.教材P93中1题:判断下列各图形中的是不是圆周角,并说明理由. 归纳:一个角是圆周角的条件:①顶点在圆上;②两边都和圆相交.
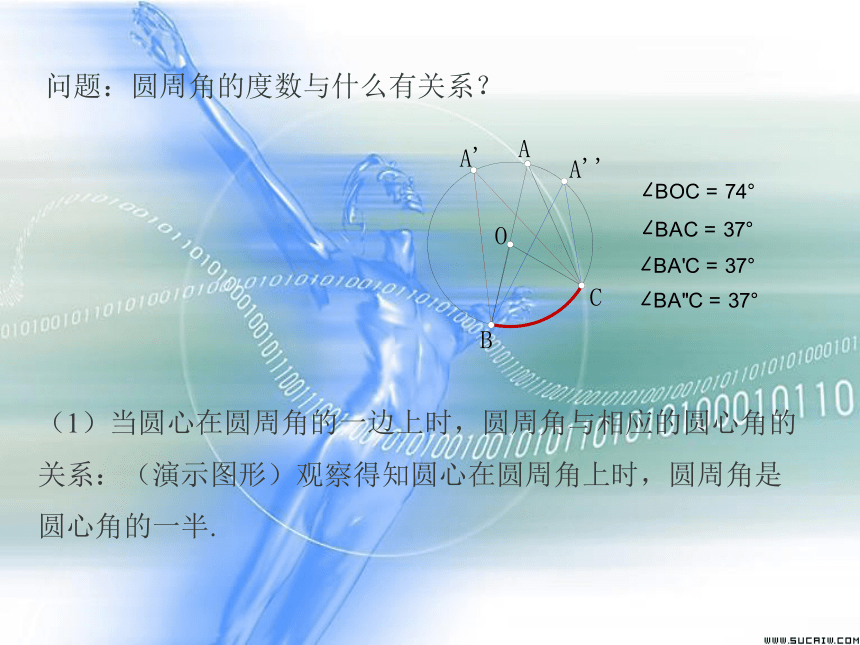
问题:圆周角的度数与什么有关系?
(1)当圆心在圆周角的一边上时,圆周角与相应的圆心角的关系:(演示图形)观察得知圆心在圆周角上时,圆周角是圆心角的一半.
证明:(圆心在圆周角上) (2)其它情况,圆周角与相应圆心角的关系: 当圆心在圆周角外部时(或在圆周角内部时)引导学生作辅助线将问题转化成圆心在圆周角一边上的情况,从而运用前面的结论,得出这时圆周角仍然等于相应的圆心角的结论.
证明:作出过C的直径(略) 圆周角定理: 一条弧所对的周角等于它所对圆心角的一半. 证明: 巩固练习:
(1)如图,已知圆心角∠AOB=100°,求圆周角∠ACB、∠ADB的度数?
(2)一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?
总结
知识:(1)圆周角定义及其两个特征;(2)圆周角定理的内容.
思想方法:一种方法和一种思想:在证明中,运用了数学中的分类方法和“化归”思想.分类时应作到不重不漏;化归思想是将复杂的问题转化成一系列的简单问题或已证问题.
作业 教材P100中 习题A组6,7,8 .
如果顶点不在圆心而在圆上,则得到如左图的新的角∠ACB,它就是圆周角。(如左图)(演示图形,提出圆周角的定义)
定义:顶点在圆周上,并且两边都和圆相
交的角叫做圆周角.
3.教材P93中1题:判断下列各图形中的是不是圆周角,并说明理由. 归纳:一个角是圆周角的条件:①顶点在圆上;②两边都和圆相交.
问题:圆周角的度数与什么有关系?
(1)当圆心在圆周角的一边上时,圆周角与相应的圆心角的关系:(演示图形)观察得知圆心在圆周角上时,圆周角是圆心角的一半.
证明:(圆心在圆周角上) (2)其它情况,圆周角与相应圆心角的关系: 当圆心在圆周角外部时(或在圆周角内部时)引导学生作辅助线将问题转化成圆心在圆周角一边上的情况,从而运用前面的结论,得出这时圆周角仍然等于相应的圆心角的结论.
证明:作出过C的直径(略) 圆周角定理: 一条弧所对的周角等于它所对圆心角的一半. 证明: 巩固练习:
(1)如图,已知圆心角∠AOB=100°,求圆周角∠ACB、∠ADB的度数?
(2)一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?
总结
知识:(1)圆周角定义及其两个特征;(2)圆周角定理的内容.
思想方法:一种方法和一种思想:在证明中,运用了数学中的分类方法和“化归”思想.分类时应作到不重不漏;化归思想是将复杂的问题转化成一系列的简单问题或已证问题.
作业 教材P100中 习题A组6,7,8 .
