高中数学人教A版(2019)必修2 第六章 正弦定理应用 选择题专项章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 第六章 正弦定理应用 选择题专项章节综合练习题(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 21:06:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
正弦定理应用 选择题专项
一、选择题
1.(2023高一下·定远期末)在中,角,,所对的边分别为,,已知,是等腰三角形则是的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
2.(2023高一下·温州期末)在中,内角,,所对的边分别是,,,已知,,,则( )
A. B.2 C. D.4
3.(2023高一下·杭州期中)圣索菲亚教堂坐落于中国黑龙江省,年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美小明为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为,在它们之间的地面上的点三点共线处测得楼顶,教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则估算索菲亚教堂的高度为( )
A. B. C. D.
4.(2023高一下·浙江期中)在中,已知,则的( )条件
A.充分不必要 B.必要不充分
C.充要 D.既不充分也不必要
5.(2023·浙江模拟)如图,某同学到野外进行实践,测量鱼塘两侧的两棵大榕树A,B之间的距离.从B处沿直线走了到达C处,测得,,则( ).
A. B. C. D.
6.(2023高三上·钦州月考)在中,内角,,的对边分别是,,,若,则等于( )
A.30° B.60° C.120° D.150°
7.(2023高三上·钦州月考)在中,内角、、所对的边分别为、、,,,,则的值等于( )
A. B. C. D.
8.(2023高三上·钦州月考)在中,角,,的对边分别为,,若,则的面积( )
A.1 B. C. D.
9.(2023高三上·钦州月考)在非钝角中,内角、、所对的边分别为、、,已知,且,则的形状为( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
10.(2022高三上·南阳期中)在中, 角,,所对的边分别为,,,,则的外接圆面积为( )
A. B. C. D.
11.(2022高三上·南阳期中)在中,,,. 若满足条件的有且只有一个,则的可能取值是( )
A. B. C. D.
12.“近水亭台草木欣,朱楼百尺回波濆”,位于济南大明湖畔的超然楼始建于元代,历代因战火及灾涝等原因,屡毁屡建.今天我们所看到的超然楼是2008年重建而成的,共有七层,站在楼上观光,可俯视整个大明湖的风景.如图,为测量超然楼的高度,选择C和一个楼房DE的楼顶为观测点,已知在水平地面上,超然楼和楼房都垂直于地面.已知,在点处测得点的仰角为,在点处测得点的仰角为,则超然楼的高度( )
A. B. C. D.
13.(2023高一下·河南月考)几何定理:以任意三角形的三条边为边,向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰为另一个等边三角形(称为拿破仑三角形)的顶点.在中,已知,,外接圆的半径为,现以其三边向外作三个等边三角形,其外接圆圆心依次记为,,,则的面积为( )
A.3 B.2 C. D.
14.(2023高一下·清远期末)在△ABC中,D为BC的中点,3sin∠ADB=2sin∠ACB,BC=6,AB=4,则△ABC的面积为( )
A.2 B.3 C.2 D.4
15.(2023高一下·海南期末)新海航大厦是中国唯一五星航空——海南航空集团总部办公楼,外形像张满的风帆,是海口市一个崭新的地标式建筑,某同学为测楼高,选取了与楼基在同一水平面内的两个测量基点与,测得,,,再通过计算得楼高为,则两个测量基点之间的距离约为( )
A.159m B.195m C.207m D.239m
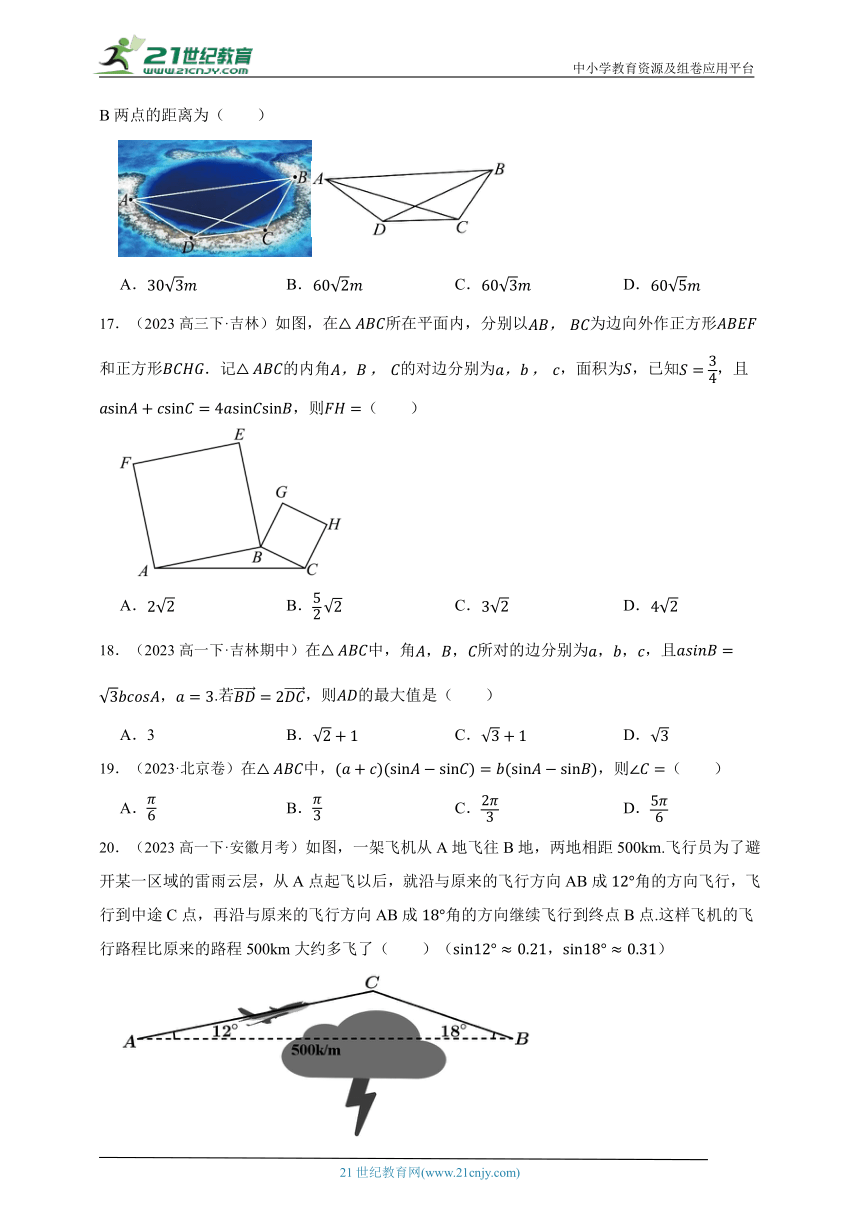
16.海洋洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞.若要测量如图所示的蓝洞的口径A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得,,,,则A、B两点的距离为( )
A. B. C. D.
17.(2023高三下·吉林)如图,在所在平面内,分别以为边向外作正方形和正方形.记的内角的对边分别为,面积为,已知,且,则( )
A. B. C. D.
18.(2023高一下·吉林期中)在中,角所对的边分别为,且.若,则的最大值是( )
A.3 B. C. D.
19.(2023·北京卷)在中,,则( )
A. B. C. D.
20.(2023高一下·安徽月考)如图,一架飞机从A地飞往B地,两地相距500km.飞行员为了避开某一区域的雷雨云层,从A点起飞以后,就沿与原来的飞行方向AB成角的方向飞行,飞行到中途C点,再沿与原来的飞行方向AB成角的方向继续飞行到终点B点.这样飞机的飞行路程比原来的路程500km大约多飞了( )(,)
A.10km B.20km C.30km D.40km
21.(2023高一下·北流期中)如图,为测得河对岸铁塔AB的高,先在河岸上选一点C,使C在铁塔底B的正东方向上,测得点A的仰角为,再由点C沿北偏东方向走10m到位置D,测得,则铁塔AB的高为
A. B. C. D.
22.(2023高一下·浙江月考)冬奥会会徽以汉字“冬”为灵感来源,结合中国书法的艺术形态,将悠久的中国传统文化底蕴与国际化风格融为一体,呈现出中国在新时代的新形象、新梦想.某同学查阅资料得知,书法中的一些特殊画笔都有固定的角度,比如在弯折位置通常采用30°、45°、60°、90°、120°、150°等特殊角度下.为了判断“冬”的弯折角度是否符合书法中的美学要求.该同学取端点绘制了,测得AB=5,BD=6,AC=4,AD=3,若点C恰好在边BD上,请帮忙计算的值( )
A. B. C. D.
23.(2023·咸阳模拟)在中,角A,B,C的对边分别是a,b,c,若,,,则的面积为( )
A. B. C. D.
24.(2023高一下·富阳月考)塔是一种在亚洲常见的,有着特定的形式和风格的中国传统建筑.最初是供奉或收藏佛骨、佛像、佛经、僧人遗体等的高耸型点式建筑,称“佛塔”.如图,为测量某塔的总高度AB,选取与塔底B在同一水平面内的两个测量基点C与D,现测得,,米,在C点测得塔顶A的仰角为60°,则塔的总高度约为( )(参考数据:,)
A.13米 B.24米 C.39米 D.45米
25.(2022高三上·浙江期中)雷峰塔又名黄妃塔 西关砖塔,位于浙江省杭州市西湖区,地处西湖风景区南岸夕照山(海拔46米)之上.是吴越国王钱俶为供奉佛螺髻发舍利 祈求国泰民安而建.始建于北宋太平兴国二年(977年),历代屡加重修.现存建筑以原雷峰塔为原型设计,重建于2002年,是“西湖十景”之一,中国九大名塔之一,中国首座彩色铜雕宝塔.李华同学为测量塔高,在西湖边相距的 两处(海拔均约16米)各放置一架垂直于地面高为米的测角仪 (如图所示).在测角仪处测得两个数据:塔顶仰角及塔顶与观测仪点的视角在测角仪处测得塔顶与观测仪点的视角,李华根据以上数据能估计雷锋塔的高度约为( )(参考数据:,)
A.70.5 B.71 C.71.5 D.72
26.(2022高二上·延安期中)如图,到达某旅游景区内的处后,有两种路径到处:一种是从处沿直线步行到处;另一种是先从处坐小火车沿直线到达处,再从处沿直线步行到处.现有甲、乙两名游客到达处后,甲沿方向匀速步行前往处,速度为50米/分钟,甲出发2分钟后,乙从处坐小火车前往处,再从处步行到处.已知小火车的速度为200米/分钟,,之间的距离为2000米,、之间的距离为3000米,,.当乙在小火车上时,甲、乙之间的直线距离最短为()
A.米 B.米 C.米 D.米
27.(2022高一下·鹤岗期末)已知△ABC的内角A,B,C的对边分别为a,b,c,则下列命题中正确的是( )
A.若 ,则△ABC为等腰三角形
B.若 , , ,则△ABC有唯一解
C.若△ABC为锐角三角形,则
D.若 , ,则△ABC面积的最大值为
28.(2023高三上·阳江开学考)在锐角中,角A,B,C的对边分别为a,b,c,的面积为S,若,则的取值范围为( )
A. B. C. D.
29.武当山,位于湖北省西北部十堰市境内,其自然风光,以雄为主,兼有险、奇、幽、秀等多重特色.主峰天柱峰犹如金铸玉瑑的宝柱雄峙苍穹,屹立于群峰之巅.环绕其周围的群山,从四面八方向主峰倾斜,形成独特的“七十二峰朝大顶,二十四涧水长流”的天然奇观,被誉为“自古无双胜境,天下第一仙山”.如图,若点为主峰天柱峰的最高点,为观测点,且在同一水平面上的投影分别为,,,由点测得点的仰角为,米,由点测得点的仰角为且,则两点到水平面的高度差约为( )(参考数据:)
A.684米 B.732米 C.746米 D.750米
30.(2023高一下·台州期末)如图,在中,D是BC的中点,E是AC上的点,,,,,则( )
A. B. C. D.
答案解析部分
1.【答案】B
【解析】【解答】解:对于 ,
由正弦定理,可得,
设,
则a=ct,b=at,c=bt,
则abc=abct3,
则t3=1,
则t=1,
则,
则a=b=c,
故△ABC为等边三角形,
故若P成立,则必有△ABC为等腰三角形,q为真命题,
反之,若q成立,p不一定成立,故 是的充分不必要条件 .
故选:B.
【分析】根据条件,结合正弦定理,可得a=b=c,再结合充分必要条件可得答案.
2.【答案】A
【解析】【解答】解:因为 ,,,,
由正弦定理可得,
故选:A.
【分析】由正弦定理,即可得出结果.
3.【答案】C
【解析】【解答】由题意知: ∠CAM=45°, ∠AMC=105°, 所以∠ACM=45°,
在Rt△ABM中, ,
在△ACM中,由正弦定理得 ,
所以 ,
由于
在Rt△DCM中,(m).
故选:C.
【分析】在Rt△ABM中由正弦得出AM,再结合△ACM中由正弦定理得到CM,进而能求CD.
4.【答案】C
【解析】【解答】充分性:若 ,有;
必要性: 在中若,由正弦定理知,.
故答案为:C
【分析】利用正弦定理和三角函数性质分析判断选项。
5.【答案】A
【解析】【解答】由题意可得,BC=100,∠BAC=15°,∠ABC=30°,所以∠ACB=135°,
,,
在△ABC中,由正弦定理可得,即,
解得.
故选:A
【分析】本题主要考查正弦定理,正弦定理与三角函数结合运算即可求解.
6.【答案】B
【解析】【解答】解:由,得a+b=c,
由余弦定理得,
又C∈(0,π),
故C=60°,
故选:B.
【分析】由正弦定理,结合已知条件化简得a+b=c,进而求得cosC,从而得答案.
7.【答案】A
【解析】【解答】解:由题意得 ,解得c=4,
由余弦定理得,
设△ABC的外接圆半径为r,由正弦定理得,
故选:A
【分析】由三角形的面积可求得c,利用余弦定理可得a,再利用正弦定理可得的值.
8.【答案】C
【解析】【解答】解:∵,
∴sinA=2sinC,
由正弦定理得a=2c=4,
∵cosB=,
∴sinB=,
∴△ABC的面积.
故选:C
【分析】由已知利用正弦定理可得a=2c=4,再利用同角三角函数基本关系求得sinB,最后根据三角形的面积公式即可计算得解.
9.【答案】A
【解析】【解答】解:∵在非钝角中,,
∴由正弦定理可得,
∵sinA≠0,
∴sinB=,
∴B=,
∵,
∴,
∴,
∴,
∴a=c,
∴A=C=B=,
∴的形状为等边三角形,
故选:A
【分析】由已知利用正弦定理得,易得B=,进而求得a=c,即可得A=C=B=,从而得结论.
10.【答案】D
【解析】【解答】由正弦定理可知,,
即
,因为,,
,根据正弦定理可知,得,
则的外接圆面积.
故答案为:D
【分析】由正弦定理和题设条件,化简得到,即,进而求得,在利用正弦定理,求得外接圆的半径,利用圆的面积公式,即可求解.
11.【答案】D
【解析】【解答】解:由正弦定理,即,所以,
因为只有一解,
若,则,
若显然满足题意,
所以或,所以或,
解得或;
故答案为:D
【分析】由正弦定理,求得,根据只有一解,分和,两种情况讨论,即可求解.
12.【答案】D
【解析】【解答】解:过作,在点处测得点的仰角为,即,,
在点处测得点的仰角为,,在中,
,,在中由正弦定理得,,
.
故答案为:D.
【分析】过作,则,在得,在中由正弦定理求,进而求.
13.【答案】C
【解析】【解答】解:在中,因为,可知,
则,可得,
又因为外接圆圆心为对应等边三角形的中心,连接,
可得,所以,
则,所以,
且,则,
根据对称性知:,所以为等边三角形,
其面积.
故答案为:C.
【分析】根据正弦定理可得的边和角,根据题意分析可得,,可知为等边三角形,进而可得面积.
14.【答案】D
【解析】【解答】如图:
易知在中由正弦定理知,设
在和由余弦定理得,,解得,,,,
.
故答案为:D
【分析】在中利用正弦定理得,在利用余弦定理计算出的长,最后利用面积公式求解。
15.【答案】B
【解析】【解答】因为,,所以,
在中由正弦定理可知,所以,
在中,所以,
所以(m).
故答案为:B.
【分析】在利用正弦定理得到,再由,得到,从而得解.
16.【答案】D
【解析】【解答】在中,,
由正弦定理,可得(m),
在中,,
所以,
在中,由余弦定理,
所以A、B两点的距离m.
故答案为:D.
【分析】根据题意利用正、余弦定理运算求解.
17.【答案】C
【解析】【解答】由正弦定理知 ,,
又 面积,,
如图连接,,
则,,,
在中由余弦定理知,.
故答案为:C
【分析】利用正弦定理结合面积公式化简 ,再由余弦定理求解 。
18.【答案】C
【解析】【解答】如图,
由,
,,,
的外接球半径为,点在弦所对应的优弧上运动,
,当,,,三点共线即经过圆心时取得最大值,
,取E为BC中点,则OE=32,ED=12,∴OD=ED2+OE2=122+322=1,
∴ AD的最大值为3+1 。
故答案为:C
【分析】利用正弦定理求出角A,再利用 △ABC 的外接球,圆内一点D与圆上点A的距离 的最值当AD经过圆心时取得。
19.【答案】B
【解析】【解答】由正弦定理知 ,
,由余弦定理,
,
故答案为:B
【分析】利用正弦定理化简再结合余弦定理求解角C。
20.【答案】B
【解析】【解答】在中,,
由正弦定理知,解得,
飞机的飞行路程比原来的路程500km大约多飞了
故选:B
【分析】结合正弦定理计算求解。
21.【答案】A
【解析】【解答】中,,,,由正弦定理得,所以,又中,,.
故答案为:A.
【分析】利用已知条件结合正弦定理得出BC的长,再结合直角三角形和正切函数的定义,进而得出AB的长。
22.【答案】D
【解析】【解答】由题意,在△ABD 中,由余弦定理,
;
因为∠ADB是三角形的内角 ,所以 ,
在△ACD 中,易得 ,
由题意,因为∠ACD 为锐角,所以
故选:D.
【分析】先根据三条边求出 ,利用平方关系得到 ,结合正弦定理可得 ,再根据平方关系可求 .
23.【答案】B
【解析】【解答】在中,由正弦定理得:,因此,
则,而,即有是正三角形,
所以的面积.
故答案为:B
【分析】利用已知条件结合正弦定理得出a的值,再结合正三角形的结构特征和b的值以及三角形的面积公式,进而得出三角形的面积。
24.【答案】C
【解析】【解答】设,则,
在中,,由正弦定理得,
因为,
代入数据,解得(米),
故答案为:C.
【分析】利用已知条件结合正切函数的定义得出BC与m的关系式,再结合正弦定理和角之间的关系式以及两角和的正弦公式,进而得出m的值。
25.【答案】C
【解析】【解答】在中,,,
所以,
由正弦定理得 ,
所以,
在直角中,,
将平面画成平面图如图所示:
由题意知:,, ,
。
故答案为:C.
【分析】利用已知条件结合正弦定理和作差法,进而估计出雷锋塔的高度。
26.【答案】B
【解析】【解答】由正弦定理可知 ,
所以 ,
又 ,
所以 ,
乙在小火车上的时间为 分钟,
设乙出发 分钟后,甲乙之间的距离为 ,则
, ,
当 时, ,
所以 ,
故答案为:B
【分析】由正弦定理和余弦定理求解即可求出甲、乙之间的直线最短距离.
27.【答案】C
【解析】【解答】解:对于A:若 , 则 ,
即sin2A=sin2B ,因为2A,2B∈(0,π) ,所以2A=2B或2A+2B=π ,
即A=B或A+B=,所以 △ABC 为等腰三角形或直角三角形,A错误;
对于B:因为 , , , 由正弦定理得, 即 ,
故sinB= ,因为b>a ,所以B>A ,故B为锐角或钝角, △ABC 有两解,故B错误;
对于C: ,
,
因为△ABC 为锐角三角形,所以 ,
所以 ,
所以
即sinA+sinB>cosA+cosB ,故C正确;
对于D:因为 , , 由余弦定理得:a2=4=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
当且仅当b=c=2时取等号,故bc≤4 ,
所以△ABC面积 ,即最大值为 ,故D错误.
故选:C
【分析】边化角后使用二倍角化简可判断A;由正弦定理及三角形大边对大角可判断选项B;根据锐角三角形可得,然后和差化积可判断C;由余弦定理及基本不等式,三角形的面积公式可判断选项D,进而可得正确选项.
28.【答案】C
【解析】【解答】解:因为,即,
所以,因为,
所以,由余弦定理,
可得,
再由正弦定理得,
因为,
所以,所以或,
得或(舍去).
因为是锐角三角形,则,解得,
令,
所以
可知在上单调递增,且,
所以的取值范围为,即的取值范围为.
故答案为:C.
【分析】结合面积公式,可得出,由余弦定理得出,再用正弦定理化边为角,得出,把所求式子用角A表示,并求出角A范围,最后结合对勾函数运算求解.
29.【答案】C
【解析】【解答】解:由题可知,,,
由点M测得点N的仰角为15°,米,由点N测得点P的仰角为a且,
如图,
过M作交NF于C,过N作交PQ于D,
如图所示, 因为, 所以 ,
又,则,、
,
则,
又,,所以,
,
由正弦定理,
可得,化简可得
即,
又,所以,
则,
则两点到水平面的高度差约为,
故答案为:C.
【分析】如图,作出辅助线,过M作交NF于C,过N作交PQ于D,根据正弦定理即可求解
30.【答案】D
【解析】【解答】设,则,
在中,由正弦定理可得,则,
在中,由正弦定理可得,即,
在中,由正弦定理可得,即,
整理得:,即,
在中,由余弦定理可得,
即,
在中,由余弦定理可得,
即,
解得,则,
在中,由余弦定理可得,
即,
可得,解得或(舍去).
故答案为:D.
【分析】根据题意利用正、余弦定理定理建立边角关系,结合倍角公式列方程求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
正弦定理应用 选择题专项
一、选择题
1.(2023高一下·定远期末)在中,角,,所对的边分别为,,已知,是等腰三角形则是的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
2.(2023高一下·温州期末)在中,内角,,所对的边分别是,,,已知,,,则( )
A. B.2 C. D.4
3.(2023高一下·杭州期中)圣索菲亚教堂坐落于中国黑龙江省,年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美小明为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为,在它们之间的地面上的点三点共线处测得楼顶,教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则估算索菲亚教堂的高度为( )
A. B. C. D.
4.(2023高一下·浙江期中)在中,已知,则的( )条件
A.充分不必要 B.必要不充分
C.充要 D.既不充分也不必要
5.(2023·浙江模拟)如图,某同学到野外进行实践,测量鱼塘两侧的两棵大榕树A,B之间的距离.从B处沿直线走了到达C处,测得,,则( ).
A. B. C. D.
6.(2023高三上·钦州月考)在中,内角,,的对边分别是,,,若,则等于( )
A.30° B.60° C.120° D.150°
7.(2023高三上·钦州月考)在中,内角、、所对的边分别为、、,,,,则的值等于( )
A. B. C. D.
8.(2023高三上·钦州月考)在中,角,,的对边分别为,,若,则的面积( )
A.1 B. C. D.
9.(2023高三上·钦州月考)在非钝角中,内角、、所对的边分别为、、,已知,且,则的形状为( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
10.(2022高三上·南阳期中)在中, 角,,所对的边分别为,,,,则的外接圆面积为( )
A. B. C. D.
11.(2022高三上·南阳期中)在中,,,. 若满足条件的有且只有一个,则的可能取值是( )
A. B. C. D.
12.“近水亭台草木欣,朱楼百尺回波濆”,位于济南大明湖畔的超然楼始建于元代,历代因战火及灾涝等原因,屡毁屡建.今天我们所看到的超然楼是2008年重建而成的,共有七层,站在楼上观光,可俯视整个大明湖的风景.如图,为测量超然楼的高度,选择C和一个楼房DE的楼顶为观测点,已知在水平地面上,超然楼和楼房都垂直于地面.已知,在点处测得点的仰角为,在点处测得点的仰角为,则超然楼的高度( )
A. B. C. D.
13.(2023高一下·河南月考)几何定理:以任意三角形的三条边为边,向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰为另一个等边三角形(称为拿破仑三角形)的顶点.在中,已知,,外接圆的半径为,现以其三边向外作三个等边三角形,其外接圆圆心依次记为,,,则的面积为( )
A.3 B.2 C. D.
14.(2023高一下·清远期末)在△ABC中,D为BC的中点,3sin∠ADB=2sin∠ACB,BC=6,AB=4,则△ABC的面积为( )
A.2 B.3 C.2 D.4
15.(2023高一下·海南期末)新海航大厦是中国唯一五星航空——海南航空集团总部办公楼,外形像张满的风帆,是海口市一个崭新的地标式建筑,某同学为测楼高,选取了与楼基在同一水平面内的两个测量基点与,测得,,,再通过计算得楼高为,则两个测量基点之间的距离约为( )
A.159m B.195m C.207m D.239m
16.海洋洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞.若要测量如图所示的蓝洞的口径A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得,,,,则A、B两点的距离为( )
A. B. C. D.
17.(2023高三下·吉林)如图,在所在平面内,分别以为边向外作正方形和正方形.记的内角的对边分别为,面积为,已知,且,则( )
A. B. C. D.
18.(2023高一下·吉林期中)在中,角所对的边分别为,且.若,则的最大值是( )
A.3 B. C. D.
19.(2023·北京卷)在中,,则( )
A. B. C. D.
20.(2023高一下·安徽月考)如图,一架飞机从A地飞往B地,两地相距500km.飞行员为了避开某一区域的雷雨云层,从A点起飞以后,就沿与原来的飞行方向AB成角的方向飞行,飞行到中途C点,再沿与原来的飞行方向AB成角的方向继续飞行到终点B点.这样飞机的飞行路程比原来的路程500km大约多飞了( )(,)
A.10km B.20km C.30km D.40km
21.(2023高一下·北流期中)如图,为测得河对岸铁塔AB的高,先在河岸上选一点C,使C在铁塔底B的正东方向上,测得点A的仰角为,再由点C沿北偏东方向走10m到位置D,测得,则铁塔AB的高为
A. B. C. D.
22.(2023高一下·浙江月考)冬奥会会徽以汉字“冬”为灵感来源,结合中国书法的艺术形态,将悠久的中国传统文化底蕴与国际化风格融为一体,呈现出中国在新时代的新形象、新梦想.某同学查阅资料得知,书法中的一些特殊画笔都有固定的角度,比如在弯折位置通常采用30°、45°、60°、90°、120°、150°等特殊角度下.为了判断“冬”的弯折角度是否符合书法中的美学要求.该同学取端点绘制了,测得AB=5,BD=6,AC=4,AD=3,若点C恰好在边BD上,请帮忙计算的值( )
A. B. C. D.
23.(2023·咸阳模拟)在中,角A,B,C的对边分别是a,b,c,若,,,则的面积为( )
A. B. C. D.
24.(2023高一下·富阳月考)塔是一种在亚洲常见的,有着特定的形式和风格的中国传统建筑.最初是供奉或收藏佛骨、佛像、佛经、僧人遗体等的高耸型点式建筑,称“佛塔”.如图,为测量某塔的总高度AB,选取与塔底B在同一水平面内的两个测量基点C与D,现测得,,米,在C点测得塔顶A的仰角为60°,则塔的总高度约为( )(参考数据:,)
A.13米 B.24米 C.39米 D.45米
25.(2022高三上·浙江期中)雷峰塔又名黄妃塔 西关砖塔,位于浙江省杭州市西湖区,地处西湖风景区南岸夕照山(海拔46米)之上.是吴越国王钱俶为供奉佛螺髻发舍利 祈求国泰民安而建.始建于北宋太平兴国二年(977年),历代屡加重修.现存建筑以原雷峰塔为原型设计,重建于2002年,是“西湖十景”之一,中国九大名塔之一,中国首座彩色铜雕宝塔.李华同学为测量塔高,在西湖边相距的 两处(海拔均约16米)各放置一架垂直于地面高为米的测角仪 (如图所示).在测角仪处测得两个数据:塔顶仰角及塔顶与观测仪点的视角在测角仪处测得塔顶与观测仪点的视角,李华根据以上数据能估计雷锋塔的高度约为( )(参考数据:,)
A.70.5 B.71 C.71.5 D.72
26.(2022高二上·延安期中)如图,到达某旅游景区内的处后,有两种路径到处:一种是从处沿直线步行到处;另一种是先从处坐小火车沿直线到达处,再从处沿直线步行到处.现有甲、乙两名游客到达处后,甲沿方向匀速步行前往处,速度为50米/分钟,甲出发2分钟后,乙从处坐小火车前往处,再从处步行到处.已知小火车的速度为200米/分钟,,之间的距离为2000米,、之间的距离为3000米,,.当乙在小火车上时,甲、乙之间的直线距离最短为()
A.米 B.米 C.米 D.米
27.(2022高一下·鹤岗期末)已知△ABC的内角A,B,C的对边分别为a,b,c,则下列命题中正确的是( )
A.若 ,则△ABC为等腰三角形
B.若 , , ,则△ABC有唯一解
C.若△ABC为锐角三角形,则
D.若 , ,则△ABC面积的最大值为
28.(2023高三上·阳江开学考)在锐角中,角A,B,C的对边分别为a,b,c,的面积为S,若,则的取值范围为( )
A. B. C. D.
29.武当山,位于湖北省西北部十堰市境内,其自然风光,以雄为主,兼有险、奇、幽、秀等多重特色.主峰天柱峰犹如金铸玉瑑的宝柱雄峙苍穹,屹立于群峰之巅.环绕其周围的群山,从四面八方向主峰倾斜,形成独特的“七十二峰朝大顶,二十四涧水长流”的天然奇观,被誉为“自古无双胜境,天下第一仙山”.如图,若点为主峰天柱峰的最高点,为观测点,且在同一水平面上的投影分别为,,,由点测得点的仰角为,米,由点测得点的仰角为且,则两点到水平面的高度差约为( )(参考数据:)
A.684米 B.732米 C.746米 D.750米
30.(2023高一下·台州期末)如图,在中,D是BC的中点,E是AC上的点,,,,,则( )
A. B. C. D.
答案解析部分
1.【答案】B
【解析】【解答】解:对于 ,
由正弦定理,可得,
设,
则a=ct,b=at,c=bt,
则abc=abct3,
则t3=1,
则t=1,
则,
则a=b=c,
故△ABC为等边三角形,
故若P成立,则必有△ABC为等腰三角形,q为真命题,
反之,若q成立,p不一定成立,故 是的充分不必要条件 .
故选:B.
【分析】根据条件,结合正弦定理,可得a=b=c,再结合充分必要条件可得答案.
2.【答案】A
【解析】【解答】解:因为 ,,,,
由正弦定理可得,
故选:A.
【分析】由正弦定理,即可得出结果.
3.【答案】C
【解析】【解答】由题意知: ∠CAM=45°, ∠AMC=105°, 所以∠ACM=45°,
在Rt△ABM中, ,
在△ACM中,由正弦定理得 ,
所以 ,
由于
在Rt△DCM中,(m).
故选:C.
【分析】在Rt△ABM中由正弦得出AM,再结合△ACM中由正弦定理得到CM,进而能求CD.
4.【答案】C
【解析】【解答】充分性:若 ,有;
必要性: 在中若,由正弦定理知,.
故答案为:C
【分析】利用正弦定理和三角函数性质分析判断选项。
5.【答案】A
【解析】【解答】由题意可得,BC=100,∠BAC=15°,∠ABC=30°,所以∠ACB=135°,
,,
在△ABC中,由正弦定理可得,即,
解得.
故选:A
【分析】本题主要考查正弦定理,正弦定理与三角函数结合运算即可求解.
6.【答案】B
【解析】【解答】解:由,得a+b=c,
由余弦定理得,
又C∈(0,π),
故C=60°,
故选:B.
【分析】由正弦定理,结合已知条件化简得a+b=c,进而求得cosC,从而得答案.
7.【答案】A
【解析】【解答】解:由题意得 ,解得c=4,
由余弦定理得,
设△ABC的外接圆半径为r,由正弦定理得,
故选:A
【分析】由三角形的面积可求得c,利用余弦定理可得a,再利用正弦定理可得的值.
8.【答案】C
【解析】【解答】解:∵,
∴sinA=2sinC,
由正弦定理得a=2c=4,
∵cosB=,
∴sinB=,
∴△ABC的面积.
故选:C
【分析】由已知利用正弦定理可得a=2c=4,再利用同角三角函数基本关系求得sinB,最后根据三角形的面积公式即可计算得解.
9.【答案】A
【解析】【解答】解:∵在非钝角中,,
∴由正弦定理可得,
∵sinA≠0,
∴sinB=,
∴B=,
∵,
∴,
∴,
∴,
∴a=c,
∴A=C=B=,
∴的形状为等边三角形,
故选:A
【分析】由已知利用正弦定理得,易得B=,进而求得a=c,即可得A=C=B=,从而得结论.
10.【答案】D
【解析】【解答】由正弦定理可知,,
即
,因为,,
,根据正弦定理可知,得,
则的外接圆面积.
故答案为:D
【分析】由正弦定理和题设条件,化简得到,即,进而求得,在利用正弦定理,求得外接圆的半径,利用圆的面积公式,即可求解.
11.【答案】D
【解析】【解答】解:由正弦定理,即,所以,
因为只有一解,
若,则,
若显然满足题意,
所以或,所以或,
解得或;
故答案为:D
【分析】由正弦定理,求得,根据只有一解,分和,两种情况讨论,即可求解.
12.【答案】D
【解析】【解答】解:过作,在点处测得点的仰角为,即,,
在点处测得点的仰角为,,在中,
,,在中由正弦定理得,,
.
故答案为:D.
【分析】过作,则,在得,在中由正弦定理求,进而求.
13.【答案】C
【解析】【解答】解:在中,因为,可知,
则,可得,
又因为外接圆圆心为对应等边三角形的中心,连接,
可得,所以,
则,所以,
且,则,
根据对称性知:,所以为等边三角形,
其面积.
故答案为:C.
【分析】根据正弦定理可得的边和角,根据题意分析可得,,可知为等边三角形,进而可得面积.
14.【答案】D
【解析】【解答】如图:
易知在中由正弦定理知,设
在和由余弦定理得,,解得,,,,
.
故答案为:D
【分析】在中利用正弦定理得,在利用余弦定理计算出的长,最后利用面积公式求解。
15.【答案】B
【解析】【解答】因为,,所以,
在中由正弦定理可知,所以,
在中,所以,
所以(m).
故答案为:B.
【分析】在利用正弦定理得到,再由,得到,从而得解.
16.【答案】D
【解析】【解答】在中,,
由正弦定理,可得(m),
在中,,
所以,
在中,由余弦定理,
所以A、B两点的距离m.
故答案为:D.
【分析】根据题意利用正、余弦定理运算求解.
17.【答案】C
【解析】【解答】由正弦定理知 ,,
又 面积,,
如图连接,,
则,,,
在中由余弦定理知,.
故答案为:C
【分析】利用正弦定理结合面积公式化简 ,再由余弦定理求解 。
18.【答案】C
【解析】【解答】如图,
由,
,,,
的外接球半径为,点在弦所对应的优弧上运动,
,当,,,三点共线即经过圆心时取得最大值,
,取E为BC中点,则OE=32,ED=12,∴OD=ED2+OE2=122+322=1,
∴ AD的最大值为3+1 。
故答案为:C
【分析】利用正弦定理求出角A,再利用 △ABC 的外接球,圆内一点D与圆上点A的距离 的最值当AD经过圆心时取得。
19.【答案】B
【解析】【解答】由正弦定理知 ,
,由余弦定理,
,
故答案为:B
【分析】利用正弦定理化简再结合余弦定理求解角C。
20.【答案】B
【解析】【解答】在中,,
由正弦定理知,解得,
飞机的飞行路程比原来的路程500km大约多飞了
故选:B
【分析】结合正弦定理计算求解。
21.【答案】A
【解析】【解答】中,,,,由正弦定理得,所以,又中,,.
故答案为:A.
【分析】利用已知条件结合正弦定理得出BC的长,再结合直角三角形和正切函数的定义,进而得出AB的长。
22.【答案】D
【解析】【解答】由题意,在△ABD 中,由余弦定理,
;
因为∠ADB是三角形的内角 ,所以 ,
在△ACD 中,易得 ,
由题意,因为∠ACD 为锐角,所以
故选:D.
【分析】先根据三条边求出 ,利用平方关系得到 ,结合正弦定理可得 ,再根据平方关系可求 .
23.【答案】B
【解析】【解答】在中,由正弦定理得:,因此,
则,而,即有是正三角形,
所以的面积.
故答案为:B
【分析】利用已知条件结合正弦定理得出a的值,再结合正三角形的结构特征和b的值以及三角形的面积公式,进而得出三角形的面积。
24.【答案】C
【解析】【解答】设,则,
在中,,由正弦定理得,
因为,
代入数据,解得(米),
故答案为:C.
【分析】利用已知条件结合正切函数的定义得出BC与m的关系式,再结合正弦定理和角之间的关系式以及两角和的正弦公式,进而得出m的值。
25.【答案】C
【解析】【解答】在中,,,
所以,
由正弦定理得 ,
所以,
在直角中,,
将平面画成平面图如图所示:
由题意知:,, ,
。
故答案为:C.
【分析】利用已知条件结合正弦定理和作差法,进而估计出雷锋塔的高度。
26.【答案】B
【解析】【解答】由正弦定理可知 ,
所以 ,
又 ,
所以 ,
乙在小火车上的时间为 分钟,
设乙出发 分钟后,甲乙之间的距离为 ,则
, ,
当 时, ,
所以 ,
故答案为:B
【分析】由正弦定理和余弦定理求解即可求出甲、乙之间的直线最短距离.
27.【答案】C
【解析】【解答】解:对于A:若 , 则 ,
即sin2A=sin2B ,因为2A,2B∈(0,π) ,所以2A=2B或2A+2B=π ,
即A=B或A+B=,所以 △ABC 为等腰三角形或直角三角形,A错误;
对于B:因为 , , , 由正弦定理得, 即 ,
故sinB= ,因为b>a ,所以B>A ,故B为锐角或钝角, △ABC 有两解,故B错误;
对于C: ,
,
因为△ABC 为锐角三角形,所以 ,
所以 ,
所以
即sinA+sinB>cosA+cosB ,故C正确;
对于D:因为 , , 由余弦定理得:a2=4=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
当且仅当b=c=2时取等号,故bc≤4 ,
所以△ABC面积 ,即最大值为 ,故D错误.
故选:C
【分析】边化角后使用二倍角化简可判断A;由正弦定理及三角形大边对大角可判断选项B;根据锐角三角形可得,然后和差化积可判断C;由余弦定理及基本不等式,三角形的面积公式可判断选项D,进而可得正确选项.
28.【答案】C
【解析】【解答】解:因为,即,
所以,因为,
所以,由余弦定理,
可得,
再由正弦定理得,
因为,
所以,所以或,
得或(舍去).
因为是锐角三角形,则,解得,
令,
所以
可知在上单调递增,且,
所以的取值范围为,即的取值范围为.
故答案为:C.
【分析】结合面积公式,可得出,由余弦定理得出,再用正弦定理化边为角,得出,把所求式子用角A表示,并求出角A范围,最后结合对勾函数运算求解.
29.【答案】C
【解析】【解答】解:由题可知,,,
由点M测得点N的仰角为15°,米,由点N测得点P的仰角为a且,
如图,
过M作交NF于C,过N作交PQ于D,
如图所示, 因为, 所以 ,
又,则,、
,
则,
又,,所以,
,
由正弦定理,
可得,化简可得
即,
又,所以,
则,
则两点到水平面的高度差约为,
故答案为:C.
【分析】如图,作出辅助线,过M作交NF于C,过N作交PQ于D,根据正弦定理即可求解
30.【答案】D
【解析】【解答】设,则,
在中,由正弦定理可得,则,
在中,由正弦定理可得,即,
在中,由正弦定理可得,即,
整理得:,即,
在中,由余弦定理可得,
即,
在中,由余弦定理可得,
即,
解得,则,
在中,由余弦定理可得,
即,
可得,解得或(舍去).
故答案为:D.
【分析】根据题意利用正、余弦定理定理建立边角关系,结合倍角公式列方程求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
