2.4与圆有关的轨迹问题课件-2023-2024学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.4与圆有关的轨迹问题课件-2023-2024学年高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 18:57:13 | ||
图片预览





文档简介
(共20张PPT)
微专题
求动点的轨迹和轨迹方程
轨迹的定义:平面上一动点M,按照一定规则运动,形成的曲线叫做动点M的轨迹.
在解析几何中 , 我们常常把图形看作点的轨迹(集合).
轨迹方程的定义:点M的轨迹方程是指点M的坐标(x, y)满足的关系式.
若求“轨迹方程”,只需写出动点坐标x,y满足的关系式,注意x,y的取值范围;
若求“轨迹”,则要先求出“轨迹方程”,再说明方程的轨迹图形,注意“去杂补漏”.
求轨迹方程的关键:动中找定——在动点运动的过程中找出动点满足的不变的性质。
概念解析
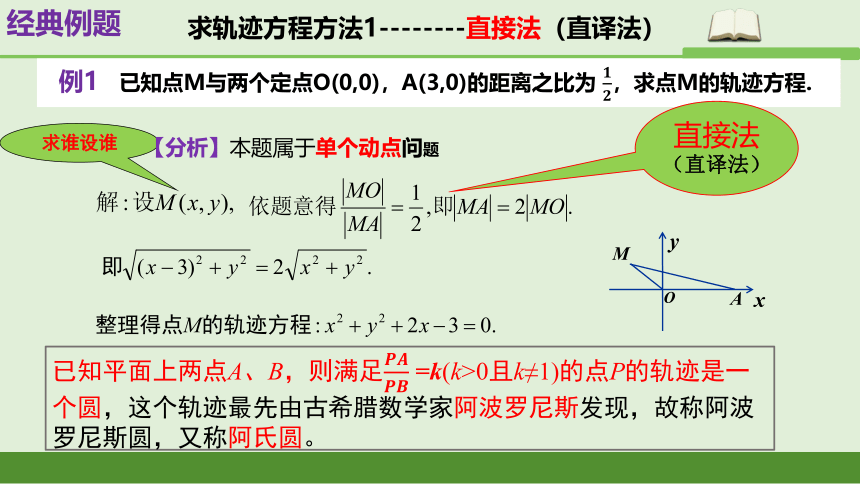
例1 已知点M与两个定点O(0,0),A(3,0)的距离之比为 ,求点M的轨迹方程.
已知平面上两点A、B,则满足 =k(k>0且k≠1)的点P的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿波罗尼斯圆,又称阿氏圆。
经典例题
直接法
(直译法)
求谁设谁
x
y
M
A
O
【分析】本题属于单个动点问题
求轨迹方程方法1--------直接法(直译法)
1. 已知一动点M到点A(-4,0)的距离是它到点B(2,0)的距离的2倍,则动点M的轨迹方程是 .
整理,得x2+y2-8x=0.
故所求动点M的轨迹方程为x2+y2-8x=0.
x2+y2-8x=0
巩固练习
(法二)以 A为原点,两定点A,B所在直线为x轴建立直角坐标系,
设A(0,0),B(6,0),M(x,y), 则|MA|2+|MB|2=26,
∴x2+y2+(x-6)2+y2=26,
化简得M点的轨迹方程为(x-3)2+y2=4
(法一) 以两定点A,B所在直线为x轴,线段AB的中垂线为y轴,建立直角坐系,
设A(-3,0),B(3,0),M(x,y), 则|MA|2+|MB|2=26,
∴(x+3)2+y2+(x-3)2+y2=26,
化简得M点的轨迹方程为x2+y2=4
2. 已知两个定点的距离为6,点M 到这两个定点的距离的平方和为26,求点M的轨迹方程.
巩固练习
B
M(x,y)
x
B
A
x
A
O
y
M(x,y)
y
P(4,3)
B
A
M
M
O
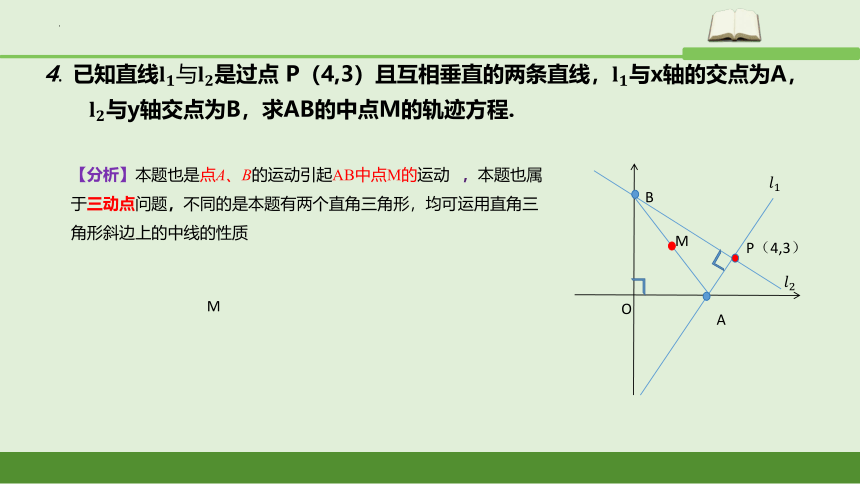
4. 已知直线是过点 P(4,3)且互相垂直的两条直线,与x轴的交点为A,与y轴交点为B,求AB的中点M的轨迹方程.
【分析】本题也是点A、B的运动引起AB中点M的运动 ,本题也属于三动点问题,不同的是本题有两个直角三角形,均可运用直角三角形斜边上的中线的性质
P
B
A
M
O
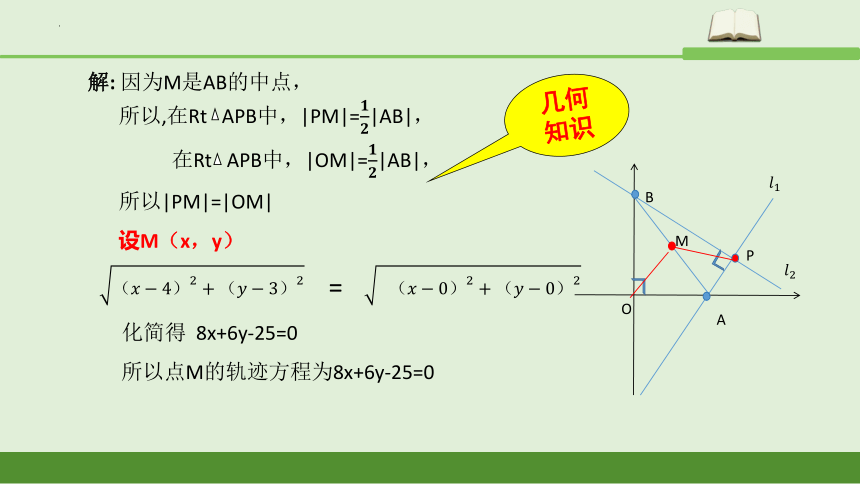
解: 因为M是AB的中点,
所以,在Rt APB中,|PM|=|AB|,
在Rt APB中,|OM|=|AB|,
所以|PM|=|OM|
设M(x,y)
=
化简得 8x+6y-25=0
所以点M的轨迹方程为8x+6y-25=0
几何知识
①建:建立平面直角坐标系;
②设:求谁的轨迹就设谁的坐标为(x,y);
③限:找限制条件,即动点满足的几何关系
④代:将点的坐标代入几何关系式中;
⑤化:化简代数式,
⑥ 去杂补漏
直接法求轨迹方程的一般步骤
注意 :建系不同, 方程不同.
归纳总结
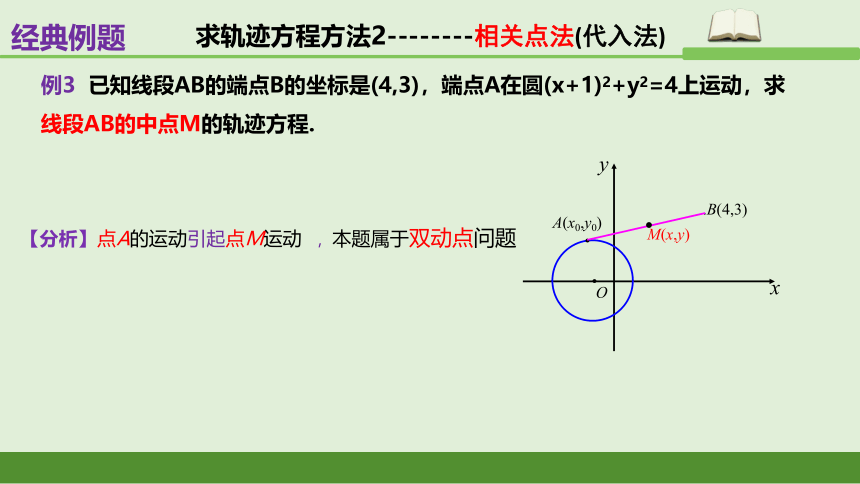
例3 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
.
O
x
y
.B(4,3)
.
A(x0,y0)
.
M(x,y)
【分析】点A的运动引起点M运动 ,本题属于双动点问题
经典例题
求轨迹方程方法2--------相关点法(代入法)
解:设点,. 因为 且是线段的中点,
所以
因为点在圆上运动,
所以点的坐标满足圆的方程,即 .
即,整理得.
这就是点的轨迹方程,它表示以为圆心,半径为的圆.
.
O
x
y
.B(4,3)
.
A(x0,y0)
.
M(x,y)
相关点法
(代入法)
求谁设谁
7.已知点P在圆C: x2+y2-8x-6y+21=0上运动,求线段OP的中点M的轨迹方程.
解:设点M(x, y), P(x0, y0)
∵点P在圆C: x2+y2-8x-6y+21=0上
∴(2x)2+(2y)2-8(2x)-6(2y)+21=0
故点M的轨迹方程为
由于M是线段OP的中点
巩固练习
8. 已知圆(x+1)2+y2=2上动点A,x轴上定点B(2,0),将BA延长到M,使AM=BA,求动点M的轨迹方程.
解:设M(x,y) A(x1,y1),,
∵AM=BA,且M在BA的延长线上,
∴A为线段MB的中点,
化简得(x+4)2+y2=8,∴点M的轨迹方程为(x+4)2+y2=8.
巩固练习
B(2,0)
A
M(x,y)
(x1,y1),
例4 长为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.
【分析】点A、B的运动引起AB中点的运动 ,本题属于三动点问题
想到初中学过的几何知识直角三角形斜边上的中线的性质-----直角三角形斜边上的中线等于???
A
O
x
y
B
M
经典例题
求轨迹方程方法3--------定义法
O
x
y
B
M
总结:当动点的运动轨迹符合圆的定义时,可利用定义直接写出动点的轨迹方程;
定义法
(先用几何知识)
解:设线段AB的中点为M,由已知得|OM|=3
所以点M的轨迹为以O为圆心半径为3的圆,
即点M的轨迹方程为
几何知识
9.等腰三角形的顶点A的坐标是(4,2),底边一端点B的坐标是(3,5),求另一个端点C的轨迹方程,并说明它是什么图形.
巩固练习
几何知识
定义法
10. 已知M(-2,0),N(2,0),求以MN为斜边的直角三角形直角顶点P的轨迹方程,并说明它是什么图形.
巩固练习
经典例题
例5
消参法
①
②
+
求轨迹方程方法4-------消参法
11. P89-10. 在平面直角坐标系中,若点P的坐标(x,y)满足,
其中θ为参数,r>0,证明:点P的轨迹是圆心为(a,b),半径为r的圆.
解:由已知得
+
得
所以
消参法
巩固练习
12. 已知当巩固练习
式 得m=x-3,代入
由
(1)直译法(直接法):建立适当的坐标系后,设动点为(x,y),根据几何条件寻求x,y之间的关系式.
求曲线方程的常见方法
(2)定义法:如果所给或由几何知识推理出的几何条件正好符合已谋曲线的定义,则可直接利用这些已知曲线的方程直接写出动点的轨迹方程.
(3)相关点法(代入法):利用所求曲线上的动点与已知曲线上动点的关系,把所求动点转换为已知动点.具体地说,就是用所求动点的坐标(x,y)来表示已知动点的坐标,并代入已知动点满足的曲线的方程,由此可求得动点坐标(x, y)满足的关系.
(4)参数法是通过消参的方法得到x与y的直接关系式
微专题
求动点的轨迹和轨迹方程
轨迹的定义:平面上一动点M,按照一定规则运动,形成的曲线叫做动点M的轨迹.
在解析几何中 , 我们常常把图形看作点的轨迹(集合).
轨迹方程的定义:点M的轨迹方程是指点M的坐标(x, y)满足的关系式.
若求“轨迹方程”,只需写出动点坐标x,y满足的关系式,注意x,y的取值范围;
若求“轨迹”,则要先求出“轨迹方程”,再说明方程的轨迹图形,注意“去杂补漏”.
求轨迹方程的关键:动中找定——在动点运动的过程中找出动点满足的不变的性质。
概念解析
例1 已知点M与两个定点O(0,0),A(3,0)的距离之比为 ,求点M的轨迹方程.
已知平面上两点A、B,则满足 =k(k>0且k≠1)的点P的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿波罗尼斯圆,又称阿氏圆。
经典例题
直接法
(直译法)
求谁设谁
x
y
M
A
O
【分析】本题属于单个动点问题
求轨迹方程方法1--------直接法(直译法)
1. 已知一动点M到点A(-4,0)的距离是它到点B(2,0)的距离的2倍,则动点M的轨迹方程是 .
整理,得x2+y2-8x=0.
故所求动点M的轨迹方程为x2+y2-8x=0.
x2+y2-8x=0
巩固练习
(法二)以 A为原点,两定点A,B所在直线为x轴建立直角坐标系,
设A(0,0),B(6,0),M(x,y), 则|MA|2+|MB|2=26,
∴x2+y2+(x-6)2+y2=26,
化简得M点的轨迹方程为(x-3)2+y2=4
(法一) 以两定点A,B所在直线为x轴,线段AB的中垂线为y轴,建立直角坐系,
设A(-3,0),B(3,0),M(x,y), 则|MA|2+|MB|2=26,
∴(x+3)2+y2+(x-3)2+y2=26,
化简得M点的轨迹方程为x2+y2=4
2. 已知两个定点的距离为6,点M 到这两个定点的距离的平方和为26,求点M的轨迹方程.
巩固练习
B
M(x,y)
x
B
A
x
A
O
y
M(x,y)
y
P(4,3)
B
A
M
M
O
4. 已知直线是过点 P(4,3)且互相垂直的两条直线,与x轴的交点为A,与y轴交点为B,求AB的中点M的轨迹方程.
【分析】本题也是点A、B的运动引起AB中点M的运动 ,本题也属于三动点问题,不同的是本题有两个直角三角形,均可运用直角三角形斜边上的中线的性质
P
B
A
M
O
解: 因为M是AB的中点,
所以,在Rt APB中,|PM|=|AB|,
在Rt APB中,|OM|=|AB|,
所以|PM|=|OM|
设M(x,y)
=
化简得 8x+6y-25=0
所以点M的轨迹方程为8x+6y-25=0
几何知识
①建:建立平面直角坐标系;
②设:求谁的轨迹就设谁的坐标为(x,y);
③限:找限制条件,即动点满足的几何关系
④代:将点的坐标代入几何关系式中;
⑤化:化简代数式,
⑥ 去杂补漏
直接法求轨迹方程的一般步骤
注意 :建系不同, 方程不同.
归纳总结
例3 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
.
O
x
y
.B(4,3)
.
A(x0,y0)
.
M(x,y)
【分析】点A的运动引起点M运动 ,本题属于双动点问题
经典例题
求轨迹方程方法2--------相关点法(代入法)
解:设点,. 因为 且是线段的中点,
所以
因为点在圆上运动,
所以点的坐标满足圆的方程,即 .
即,整理得.
这就是点的轨迹方程,它表示以为圆心,半径为的圆.
.
O
x
y
.B(4,3)
.
A(x0,y0)
.
M(x,y)
相关点法
(代入法)
求谁设谁
7.已知点P在圆C: x2+y2-8x-6y+21=0上运动,求线段OP的中点M的轨迹方程.
解:设点M(x, y), P(x0, y0)
∵点P在圆C: x2+y2-8x-6y+21=0上
∴(2x)2+(2y)2-8(2x)-6(2y)+21=0
故点M的轨迹方程为
由于M是线段OP的中点
巩固练习
8. 已知圆(x+1)2+y2=2上动点A,x轴上定点B(2,0),将BA延长到M,使AM=BA,求动点M的轨迹方程.
解:设M(x,y) A(x1,y1),,
∵AM=BA,且M在BA的延长线上,
∴A为线段MB的中点,
化简得(x+4)2+y2=8,∴点M的轨迹方程为(x+4)2+y2=8.
巩固练习
B(2,0)
A
M(x,y)
(x1,y1),
例4 长为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.
【分析】点A、B的运动引起AB中点的运动 ,本题属于三动点问题
想到初中学过的几何知识直角三角形斜边上的中线的性质-----直角三角形斜边上的中线等于???
A
O
x
y
B
M
经典例题
求轨迹方程方法3--------定义法
O
x
y
B
M
总结:当动点的运动轨迹符合圆的定义时,可利用定义直接写出动点的轨迹方程;
定义法
(先用几何知识)
解:设线段AB的中点为M,由已知得|OM|=3
所以点M的轨迹为以O为圆心半径为3的圆,
即点M的轨迹方程为
几何知识
9.等腰三角形的顶点A的坐标是(4,2),底边一端点B的坐标是(3,5),求另一个端点C的轨迹方程,并说明它是什么图形.
巩固练习
几何知识
定义法
10. 已知M(-2,0),N(2,0),求以MN为斜边的直角三角形直角顶点P的轨迹方程,并说明它是什么图形.
巩固练习
经典例题
例5
消参法
①
②
+
求轨迹方程方法4-------消参法
11. P89-10. 在平面直角坐标系中,若点P的坐标(x,y)满足,
其中θ为参数,r>0,证明:点P的轨迹是圆心为(a,b),半径为r的圆.
解:由已知得
+
得
所以
消参法
巩固练习
12. 已知当
式 得m=x-3,代入
由
(1)直译法(直接法):建立适当的坐标系后,设动点为(x,y),根据几何条件寻求x,y之间的关系式.
求曲线方程的常见方法
(2)定义法:如果所给或由几何知识推理出的几何条件正好符合已谋曲线的定义,则可直接利用这些已知曲线的方程直接写出动点的轨迹方程.
(3)相关点法(代入法):利用所求曲线上的动点与已知曲线上动点的关系,把所求动点转换为已知动点.具体地说,就是用所求动点的坐标(x,y)来表示已知动点的坐标,并代入已知动点满足的曲线的方程,由此可求得动点坐标(x, y)满足的关系.
(4)参数法是通过消参的方法得到x与y的直接关系式
