人教版三年级上册数学集合(课件)(共17张PPT)
文档属性
| 名称 | 人教版三年级上册数学集合(课件)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 20:54:17 | ||
图片预览






文档简介
(共17张PPT)
第1课时 集 合
人教版小学数学三年级上册
【教学目标】
1.在具体情境中感受集合思想,掌握填写集合圈的方法。
2.会借助直观图,利用集合思想解决简单的实际问题。
新课导入
下面是三(1)班参加跳绳、踢毽比赛的学生名单。
问题:
参加这两项比赛的共有多少人
1.观察统计表,寻找数学信息
参加跳绳比赛的有9人,参加踢毽比赛的有8人,其中有3名学生既参加了跳绳比赛又参加了踢毽比赛。
2.理解题意
要求参加这两项比赛的共有多少人,通常用加法计算,列式为9+8=17(人)。可是有3人两项比赛都参加了,总人数不是17,所以不能直接用两个数相加解决这个问题,应选择其他策略。
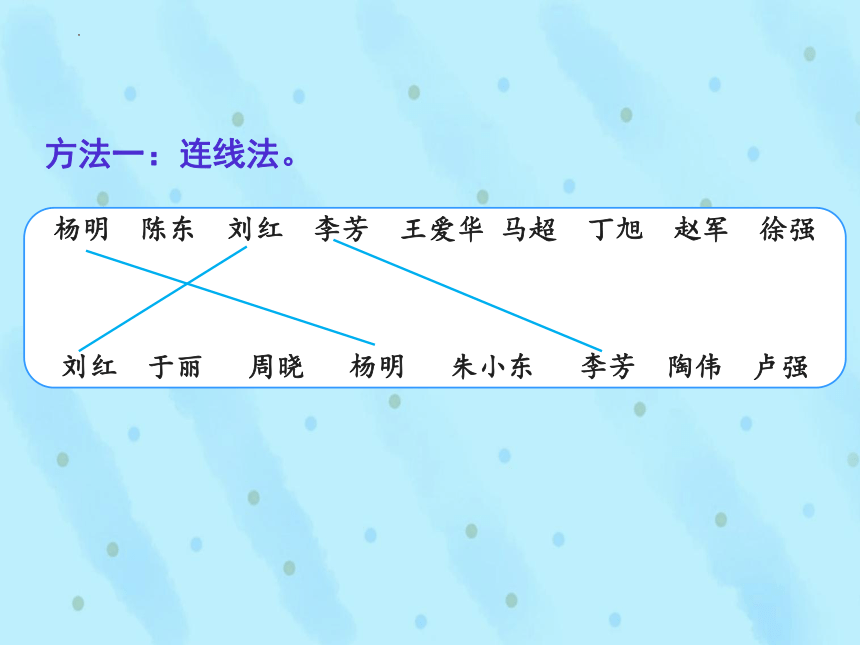
方法一:连线法。
杨明 陈东 刘红 李芳 王爱华 马超 丁旭 赵军 徐强
刘红 于丽 周晓 杨明 朱小东 李芳 陶伟 卢强
把两项比赛都参加的3名学生只数一次,就知道参加这两项比赛的一共有多少人了。
方法二:借助集合图,把两项比赛都参加的学生姓名写在两个集合圈重叠的部分里。
跳绳的学生
踢毽的学生
陈东 王爱华
马超 丁旭
赵军 徐强
于丽 周晓
朱小东
陶伟 卢强
杨明
刘红
李芳
两项都参加的学生
思路一:
从集合图中可以清楚地看出,在参加跳 绳比赛的9人中包含了两项比赛都参加的3人,在参加踢毽比赛的8人中也包含了两项比赛都参加的3人,假如列式 为9+8,这3名学生就加了两次,要减去重复计算的3人。
方法提示
填写集合图时,先将重复出现的找出来填在中间重合的部分,然后将剩余的分类依次填在剩下的集合图中。
思路二:
先求出只参加跳绳比赛(或踢毽比赛)的人数,再加上参加踢毽比赛(或跳绳比赛)的人数,就是参加这两项比赛的总人数。列式解答
方法一:9+8-3=14(人)
方法二:9一3+8=14(人)
或8-3+9=14(人)
答:参加这两项比赛的共有14人。
知识提炼
解决重叠问题时,可以先画出示意图,再借助示意图进行思考。为了不重复计算,应从两部分的和中减去重叠部分;也可以先用其中一部分减去重叠部分,再加上另一部分;还可以用一部分(不含重叠)+重叠部分+另一部分(不含重叠)。
小结:
求一个数的几分之几是多少,就是把一个物体平均分成几份,求出几份是多少。
同学们,下课!
第1课时 集 合
人教版小学数学三年级上册
【教学目标】
1.在具体情境中感受集合思想,掌握填写集合圈的方法。
2.会借助直观图,利用集合思想解决简单的实际问题。
新课导入
下面是三(1)班参加跳绳、踢毽比赛的学生名单。
问题:
参加这两项比赛的共有多少人
1.观察统计表,寻找数学信息
参加跳绳比赛的有9人,参加踢毽比赛的有8人,其中有3名学生既参加了跳绳比赛又参加了踢毽比赛。
2.理解题意
要求参加这两项比赛的共有多少人,通常用加法计算,列式为9+8=17(人)。可是有3人两项比赛都参加了,总人数不是17,所以不能直接用两个数相加解决这个问题,应选择其他策略。
方法一:连线法。
杨明 陈东 刘红 李芳 王爱华 马超 丁旭 赵军 徐强
刘红 于丽 周晓 杨明 朱小东 李芳 陶伟 卢强
把两项比赛都参加的3名学生只数一次,就知道参加这两项比赛的一共有多少人了。
方法二:借助集合图,把两项比赛都参加的学生姓名写在两个集合圈重叠的部分里。
跳绳的学生
踢毽的学生
陈东 王爱华
马超 丁旭
赵军 徐强
于丽 周晓
朱小东
陶伟 卢强
杨明
刘红
李芳
两项都参加的学生
思路一:
从集合图中可以清楚地看出,在参加跳 绳比赛的9人中包含了两项比赛都参加的3人,在参加踢毽比赛的8人中也包含了两项比赛都参加的3人,假如列式 为9+8,这3名学生就加了两次,要减去重复计算的3人。
方法提示
填写集合图时,先将重复出现的找出来填在中间重合的部分,然后将剩余的分类依次填在剩下的集合图中。
思路二:
先求出只参加跳绳比赛(或踢毽比赛)的人数,再加上参加踢毽比赛(或跳绳比赛)的人数,就是参加这两项比赛的总人数。列式解答
方法一:9+8-3=14(人)
方法二:9一3+8=14(人)
或8-3+9=14(人)
答:参加这两项比赛的共有14人。
知识提炼
解决重叠问题时,可以先画出示意图,再借助示意图进行思考。为了不重复计算,应从两部分的和中减去重叠部分;也可以先用其中一部分减去重叠部分,再加上另一部分;还可以用一部分(不含重叠)+重叠部分+另一部分(不含重叠)。
小结:
求一个数的几分之几是多少,就是把一个物体平均分成几份,求出几份是多少。
同学们,下课!
