人教版数学7年级下册 7.1 平面直角坐标系 课时练 (含解析)
文档属性
| 名称 | 人教版数学7年级下册 7.1 平面直角坐标系 课时练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 624.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 18:46:57 | ||
图片预览


文档简介
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.1 有序数对
1.小敏出学校向南走1500 m,再向东走2000 m到家,如果以学校位置为原点,以正东、正北方向为轴、轴正方向建立平面直角坐标系,规定一个单位长度代表1 m,则小敏家用有序数对表示为( )
A. B.
C. D.
2.数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如,为实数)的数叫做复数,用表示,任何一个复数在平面直角坐标系中都可以用有序数对表示,如:表示为,则可表示为( )
A. B. C. D.
3.第二列第一行用数对表示,数对和表示的位置是( )
A.同一行 B.同一列 C.同行同列 D.不同行不同列
4.如图为一个围棋棋盘的一部分,如果白棋②用数对表示为,白棋④用数对表示为,那么黑棋用数对表示为 __________.
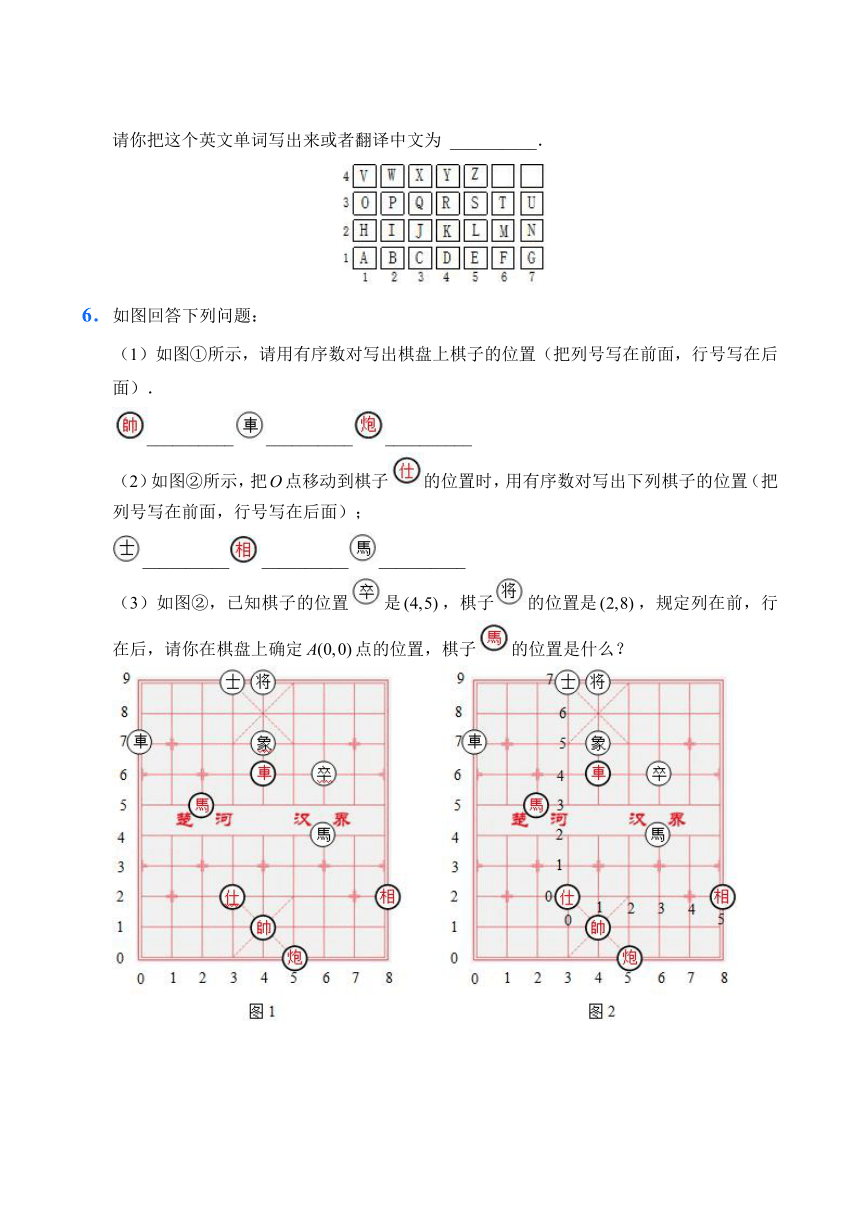
5.有一个英文单词的字母顺序对应如图中的有序数对分别为,,,,,请你把这个英文单词写出来或者翻译中文为 __________.
6.如图回答下列问题:
(1)如图①所示,请用有序数对写出棋盘上棋子的位置(把列号写在前面,行号写在后面).
______________________________
(2)如图②所示,把点移动到棋子的位置时,用有序数对写出下列棋子的位置(把列号写在前面,行号写在后面);
______________________________
(3)如图②,已知棋子的位置是,棋子的位置是,规定列在前,行在后,请你在棋盘上确定点的位置,棋子的位置是什么?
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.1 有序数对
1.【答案】B
【解析】学校大门所在的位置为原点,分别以正东、正北方向为,轴正方向建立平面直角坐标系,所以学校大门的坐标是,小敏家的坐标是,故选B.
2.【答案】B
【解析】由题意,得可表示为.故选B.
3.【答案】B
【解析】第二列第一行用数对表示,则数对表示第三列,第六行,数对表示表示第三列,第四行.所以数对和表示的位置是同一列不同行.故选B.
4.【答案】
【解析】如图所示:黑棋用数对表示为(1,).故答案为:.
5.【答案】CHINA或中国
【解析】(3,1)对应C,(1,12)对应H,(2,2)对应I,
(7,2)对应N,(1,1)对应A,∴这个单词是CHINA.
故答案为:CHINA或中国.
6.【解析】(1)由图①可得,的位置为,的位置为,的位置为,
故答案为:,,;
(2)由图②可得,的位置为,的位置为,的位置为,
故答案为:,,;
(3)如图2所示,点即为所求,棋子的位置为.
7.1.2 坐标平面内点的坐标特征
1.点在第四象限,且到轴的距离为3,则的值为( )
A. B.
C.1 D.2
2.如果点在轴上,那么点所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.若点在第二象限,则点在第( )象限.
A.一 B.二
C.三 D.四
4.在平面直角坐标系中,点在轴上,则点的坐标为( )
A. B.
C. D.
5.点到轴的距离为 __________,到轴的距离为 __________.
6.在平面直角坐标系中,若点在第四象限,且点到轴和轴距离分别为5和4,则点的坐标为 __________.
7.已知点.
(1)若点在轴上,求的值;
(2)若点到轴的距离是到轴距离的2倍,求点的坐标.
8.已知平面直角坐标系中有一点.
(1)点在二、四象限的角平分线上,求点的坐标;
(2)点到轴的距离为1时,求点的坐标.
7.1.2 坐标平面内点的坐标特征
1.【答案】A
【解析】由点在第四象限,且到轴的距离为3,得点的横坐标是3,
∴,解得.故选A.
2.【答案】D
【解析】因为点在轴上,所以,解得,所以,,所以点所在的象限是第四象限.故选D.
3.【答案】C
【解析】∵点在第二象限,∴,,∴,∴点在第三象限.故选C.
4.【答案】A
【解析】∵点在平面直角坐标系的轴上,∴,解得,
∴,点的坐标为.故选A.
5.【答案】5,2
【解析】∵,,∴点到轴的距离是5,到轴的距离是2.故答案为:5,2.
6.【答案】
【解析】∵点在第四象限,且点到轴和轴的距离分别为5,4,∴点的横坐标是4,纵坐标是,即点的坐标为.故答案为:.
7.【解析】(1)∵点在轴上,
∴,
解得:.
(2)∵点到轴的距离是到轴距离的2倍,
∴,
∴或,
解得:或,
∴或.
8.【解析】(1)∵点在二、四象限的角平分线上,
,
∴,
∴点坐标为,;
(2)∵点到轴的距离为1,
∴,
∴或,
解得:或,
∴点坐标为或.
7.1 平面直角坐标系
7.1.1 有序数对
1.小敏出学校向南走1500 m,再向东走2000 m到家,如果以学校位置为原点,以正东、正北方向为轴、轴正方向建立平面直角坐标系,规定一个单位长度代表1 m,则小敏家用有序数对表示为( )
A. B.
C. D.
2.数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如,为实数)的数叫做复数,用表示,任何一个复数在平面直角坐标系中都可以用有序数对表示,如:表示为,则可表示为( )
A. B. C. D.
3.第二列第一行用数对表示,数对和表示的位置是( )
A.同一行 B.同一列 C.同行同列 D.不同行不同列
4.如图为一个围棋棋盘的一部分,如果白棋②用数对表示为,白棋④用数对表示为,那么黑棋用数对表示为 __________.
5.有一个英文单词的字母顺序对应如图中的有序数对分别为,,,,,请你把这个英文单词写出来或者翻译中文为 __________.
6.如图回答下列问题:
(1)如图①所示,请用有序数对写出棋盘上棋子的位置(把列号写在前面,行号写在后面).
______________________________
(2)如图②所示,把点移动到棋子的位置时,用有序数对写出下列棋子的位置(把列号写在前面,行号写在后面);
______________________________
(3)如图②,已知棋子的位置是,棋子的位置是,规定列在前,行在后,请你在棋盘上确定点的位置,棋子的位置是什么?
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.1 有序数对
1.【答案】B
【解析】学校大门所在的位置为原点,分别以正东、正北方向为,轴正方向建立平面直角坐标系,所以学校大门的坐标是,小敏家的坐标是,故选B.
2.【答案】B
【解析】由题意,得可表示为.故选B.
3.【答案】B
【解析】第二列第一行用数对表示,则数对表示第三列,第六行,数对表示表示第三列,第四行.所以数对和表示的位置是同一列不同行.故选B.
4.【答案】
【解析】如图所示:黑棋用数对表示为(1,).故答案为:.
5.【答案】CHINA或中国
【解析】(3,1)对应C,(1,12)对应H,(2,2)对应I,
(7,2)对应N,(1,1)对应A,∴这个单词是CHINA.
故答案为:CHINA或中国.
6.【解析】(1)由图①可得,的位置为,的位置为,的位置为,
故答案为:,,;
(2)由图②可得,的位置为,的位置为,的位置为,
故答案为:,,;
(3)如图2所示,点即为所求,棋子的位置为.
7.1.2 坐标平面内点的坐标特征
1.点在第四象限,且到轴的距离为3,则的值为( )
A. B.
C.1 D.2
2.如果点在轴上,那么点所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.若点在第二象限,则点在第( )象限.
A.一 B.二
C.三 D.四
4.在平面直角坐标系中,点在轴上,则点的坐标为( )
A. B.
C. D.
5.点到轴的距离为 __________,到轴的距离为 __________.
6.在平面直角坐标系中,若点在第四象限,且点到轴和轴距离分别为5和4,则点的坐标为 __________.
7.已知点.
(1)若点在轴上,求的值;
(2)若点到轴的距离是到轴距离的2倍,求点的坐标.
8.已知平面直角坐标系中有一点.
(1)点在二、四象限的角平分线上,求点的坐标;
(2)点到轴的距离为1时,求点的坐标.
7.1.2 坐标平面内点的坐标特征
1.【答案】A
【解析】由点在第四象限,且到轴的距离为3,得点的横坐标是3,
∴,解得.故选A.
2.【答案】D
【解析】因为点在轴上,所以,解得,所以,,所以点所在的象限是第四象限.故选D.
3.【答案】C
【解析】∵点在第二象限,∴,,∴,∴点在第三象限.故选C.
4.【答案】A
【解析】∵点在平面直角坐标系的轴上,∴,解得,
∴,点的坐标为.故选A.
5.【答案】5,2
【解析】∵,,∴点到轴的距离是5,到轴的距离是2.故答案为:5,2.
6.【答案】
【解析】∵点在第四象限,且点到轴和轴的距离分别为5,4,∴点的横坐标是4,纵坐标是,即点的坐标为.故答案为:.
7.【解析】(1)∵点在轴上,
∴,
解得:.
(2)∵点到轴的距离是到轴距离的2倍,
∴,
∴或,
解得:或,
∴或.
8.【解析】(1)∵点在二、四象限的角平分线上,
,
∴,
∴点坐标为,;
(2)∵点到轴的距离为1,
∴,
∴或,
解得:或,
∴点坐标为或.
