第二十五章 概率初步 单元练习(含答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十五章 概率初步 单元练习(含答案) 2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 16:50:12 | ||
图片预览


文档简介
第二十五章 概率初步
一、选择题
1.下列成语所描述的事件中,是随机事件的是( )
A.水涨船高 B.水中捞月 C.一步登天 D.一箭双雕
2.在一个不透明的袋子里,装有3个红球,2个白球,1个黄球,它们除颜色外都相同,从袋中任意摸出一个球为白球的概率是( )
A. B. C. D.
3.某商场为了吸引顾客,设计了如图所示的可自由转动的转盘,当指针指向阴影部分时,顾客可获得一份奖品,那么顾客获奖的概率为( )
A. B. C. D.
4.一个不透明的箱子里共装有m个球,其中红球5个,这些球除颜色不同外其余都相同.每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.2附近,则可以估算出m的值为( )
A.1 B.5 C.20 D.25
5.在一不透明的箱子里放有个除颜色外其他完全相同的球,其中只有4个白球,任意摸出一个球记下颜色后,放回袋中,再摇匀,再摸,通过大量重复摸球后发现,摸到白球的频率稳定在0.25,则大约是( )
A.15 B.16 C.12 D.8
6.某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率;
B.任意写一个整数,它能被2整除的概率;
C.掷一枚质地均匀正六面体骰子,向上的面点数是2的概率
D.暗箱中有1个红球和2个白球,它们只有颜色上的区别,从中任取一球是白球的概率
7.某校即将举行田径运动会,“体育达人”小明从“跳高”“跳远”“100米”“400米”四个项目中,随机选择两项,则他选择“100米”与“400米”两个项目的概率是( )
A. B. C. D.
8.在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和等于6的概率是( )
A. B. C. D.
二、填空题
9.某校为开展“永远跟党走、奋进新征程”主题党的二十大教育宣讲活动,学校从2名男老师和2名女老师中随机选取2名教师作为宣讲员,则恰好选中1名男老师和1名女老师的概率为 .
10.如图是一个转盘,转盘上共有红、黄、蓝三种不同颜色的区域,已知红色区域的圆心角为,黄色区域的圆心角为,自由转动转盘,指针落在蓝色区域的概率是 .
11.在平面直角坐标系中有五个点,分别是,,,,,从中任选一个点恰好在第一象限的概率是 .
12.一个不透明的袋子里只装有红球、黄球,总共20个,这些球除颜色外形状大小都相同.芳芳每次摸球前先将袋子里的球摇匀,任意摸出一个球记下颜色后再放回袋子,通过多次重复试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球大约有 个.
13.如图,正方形纸板中,点,,,分别为,,,中点,于点,于点,于点,于点,小明随机向纸板内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
三、解答题
14.某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
(1)当n为何值时,男生小强参加是确定事件?
(2)当n为何值时,男生小强参加是随机事件?
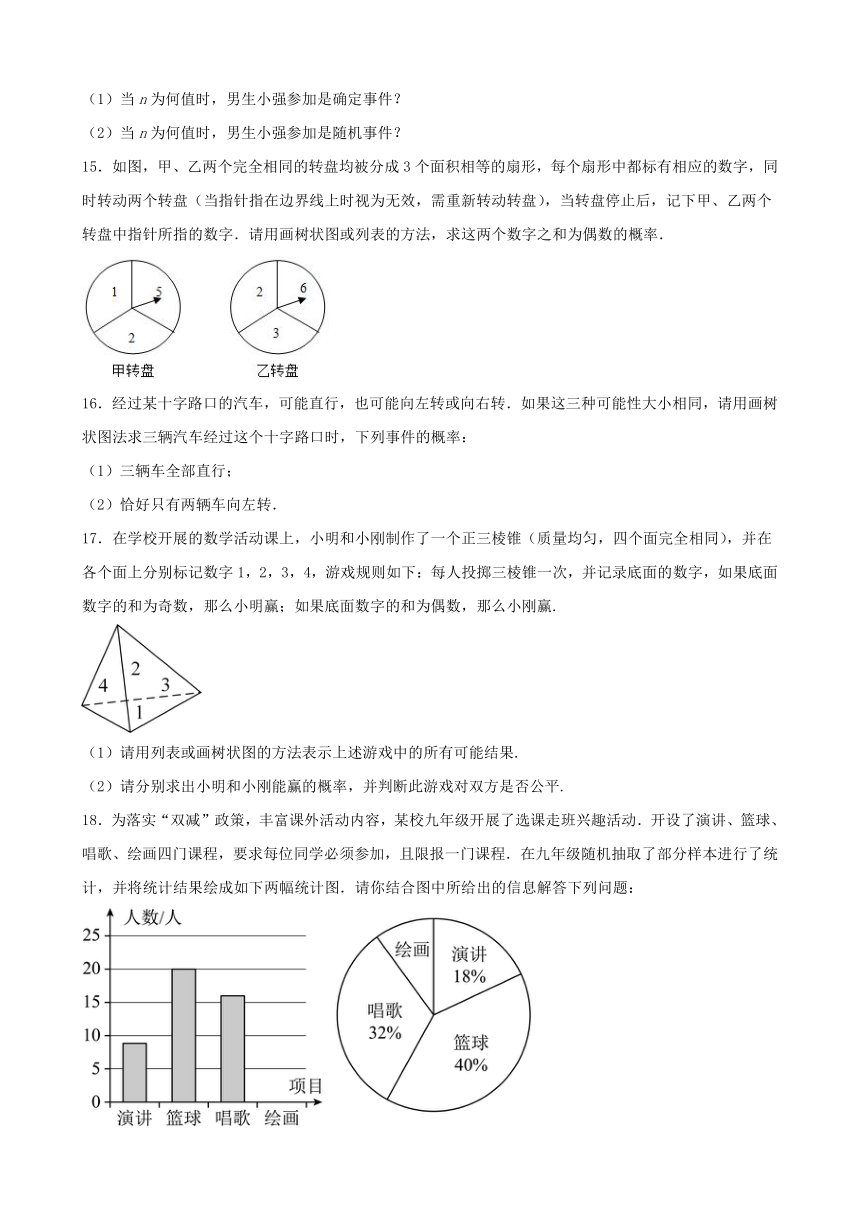
15.如图,甲、乙两个完全相同的转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,记下甲、乙两个转盘中指针所指的数字.请用画树状图或列表的方法,求这两个数字之和为偶数的概率.
16.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,请用画树状图法求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部直行;
(2)恰好只有两辆车向左转.
17.在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
(1)请用列表或画树状图的方法表示上述游戏中的所有可能结果.
(2)请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.
18.为落实“双减”政策,丰富课外活动内容,某校九年级开展了选课走班兴趣活动.开设了演讲、篮球、唱歌、绘画四门课程,要求每位同学必须参加,且限报一门课程.在九年级随机抽取了部分样本进行了统计,并将统计结果绘成如下两幅统计图.请你结合图中所给出的信息解答下列问题:
(1)所选样本的样本容量为________,扇形统计图中“绘画”对应扇形的圆心角的大小为______;
(2)若该校九年级学生有500人,请你估计选课走班活动中,参加演讲和绘画课程的学生共有多少人?
(3)若所选样本中参加绘画课程的男生为2人,其余为女生,现从中任选2人参加绘画展演,请用树状图或列表法求所选学生为1男1女的概率.
参考答案
1.D
2.C
3.D
4.D
5.B
6.C
7.C
8.D
9.
10.
11.
12.5
13. /0.5
14.解:(1)当女生选1名时,三名男生都能选上,男生小强参加是必然事件,确定事件,
当女生选4名时,三名男生都不能选上,男生小强参加是不可能事件,确定事件,
综上所述,当n=1或4时,男生小强参加是确定事件;
(2)当n=2或3时,男生小强参加是随机事件.
15.解:画树状图如下:
由树状图知,共有9种等可能结果,其中两个数字之和是偶数的有4种结果,
∴P(两个数字之和是偶数).
16.解:(1)用树状图表示出三辆车经过该十字路口时所有可能出现的情况如图:
由树状图可以看出,三辆车经过该十字路口时所有等可能出现的情况共有27种.
三辆车全部继续直行的结果只有1种,所以P(三辆车全部继续直行)=.
(2)两辆车向左转的结果有6种,所以P(两辆车向左转,一辆车向右转)==.
17.(1)解:列表如下:
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
(2)解:从图表可知,共有16种等可能的情况,其中两次所掷数字的和为奇数的情况有8种,和为偶数的有8种,
所以小明获胜的概率为、小刚获胜的概率为,
故此游戏对两人是公平的.
18.(1)这次调查的样本容量为20÷40%=50,
扇形统计图中“绘画”对应扇形的圆心角的大小为360°×(100%-32%-18%-40%)=36°,
故答案为:50;36°;
(2)人;
(3)列表如下:
男1 男2 女1 女2 女3
男1 男1男2 男1女1 男1女2 男1士3
男2 男2男1 男2女 男2女2 男2女3
女l 女1男1 女1男2 女1女2 女1女3
女2 女2男1 女1里2 女2女1 女2女3
女3 女3男1 女3男2 女3女 女3女2
任选2人参加绘画展演共有20种等可能的结果,其中1男1女共有12种,故选中1男1女的概率为:P(1男1女).
一、选择题
1.下列成语所描述的事件中,是随机事件的是( )
A.水涨船高 B.水中捞月 C.一步登天 D.一箭双雕
2.在一个不透明的袋子里,装有3个红球,2个白球,1个黄球,它们除颜色外都相同,从袋中任意摸出一个球为白球的概率是( )
A. B. C. D.
3.某商场为了吸引顾客,设计了如图所示的可自由转动的转盘,当指针指向阴影部分时,顾客可获得一份奖品,那么顾客获奖的概率为( )
A. B. C. D.
4.一个不透明的箱子里共装有m个球,其中红球5个,这些球除颜色不同外其余都相同.每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.2附近,则可以估算出m的值为( )
A.1 B.5 C.20 D.25
5.在一不透明的箱子里放有个除颜色外其他完全相同的球,其中只有4个白球,任意摸出一个球记下颜色后,放回袋中,再摇匀,再摸,通过大量重复摸球后发现,摸到白球的频率稳定在0.25,则大约是( )
A.15 B.16 C.12 D.8
6.某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率;
B.任意写一个整数,它能被2整除的概率;
C.掷一枚质地均匀正六面体骰子,向上的面点数是2的概率
D.暗箱中有1个红球和2个白球,它们只有颜色上的区别,从中任取一球是白球的概率
7.某校即将举行田径运动会,“体育达人”小明从“跳高”“跳远”“100米”“400米”四个项目中,随机选择两项,则他选择“100米”与“400米”两个项目的概率是( )
A. B. C. D.
8.在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和等于6的概率是( )
A. B. C. D.
二、填空题
9.某校为开展“永远跟党走、奋进新征程”主题党的二十大教育宣讲活动,学校从2名男老师和2名女老师中随机选取2名教师作为宣讲员,则恰好选中1名男老师和1名女老师的概率为 .
10.如图是一个转盘,转盘上共有红、黄、蓝三种不同颜色的区域,已知红色区域的圆心角为,黄色区域的圆心角为,自由转动转盘,指针落在蓝色区域的概率是 .
11.在平面直角坐标系中有五个点,分别是,,,,,从中任选一个点恰好在第一象限的概率是 .
12.一个不透明的袋子里只装有红球、黄球,总共20个,这些球除颜色外形状大小都相同.芳芳每次摸球前先将袋子里的球摇匀,任意摸出一个球记下颜色后再放回袋子,通过多次重复试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球大约有 个.
13.如图,正方形纸板中,点,,,分别为,,,中点,于点,于点,于点,于点,小明随机向纸板内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
三、解答题
14.某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
(1)当n为何值时,男生小强参加是确定事件?
(2)当n为何值时,男生小强参加是随机事件?
15.如图,甲、乙两个完全相同的转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,记下甲、乙两个转盘中指针所指的数字.请用画树状图或列表的方法,求这两个数字之和为偶数的概率.
16.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,请用画树状图法求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部直行;
(2)恰好只有两辆车向左转.
17.在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
(1)请用列表或画树状图的方法表示上述游戏中的所有可能结果.
(2)请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.
18.为落实“双减”政策,丰富课外活动内容,某校九年级开展了选课走班兴趣活动.开设了演讲、篮球、唱歌、绘画四门课程,要求每位同学必须参加,且限报一门课程.在九年级随机抽取了部分样本进行了统计,并将统计结果绘成如下两幅统计图.请你结合图中所给出的信息解答下列问题:
(1)所选样本的样本容量为________,扇形统计图中“绘画”对应扇形的圆心角的大小为______;
(2)若该校九年级学生有500人,请你估计选课走班活动中,参加演讲和绘画课程的学生共有多少人?
(3)若所选样本中参加绘画课程的男生为2人,其余为女生,现从中任选2人参加绘画展演,请用树状图或列表法求所选学生为1男1女的概率.
参考答案
1.D
2.C
3.D
4.D
5.B
6.C
7.C
8.D
9.
10.
11.
12.5
13. /0.5
14.解:(1)当女生选1名时,三名男生都能选上,男生小强参加是必然事件,确定事件,
当女生选4名时,三名男生都不能选上,男生小强参加是不可能事件,确定事件,
综上所述,当n=1或4时,男生小强参加是确定事件;
(2)当n=2或3时,男生小强参加是随机事件.
15.解:画树状图如下:
由树状图知,共有9种等可能结果,其中两个数字之和是偶数的有4种结果,
∴P(两个数字之和是偶数).
16.解:(1)用树状图表示出三辆车经过该十字路口时所有可能出现的情况如图:
由树状图可以看出,三辆车经过该十字路口时所有等可能出现的情况共有27种.
三辆车全部继续直行的结果只有1种,所以P(三辆车全部继续直行)=.
(2)两辆车向左转的结果有6种,所以P(两辆车向左转,一辆车向右转)==.
17.(1)解:列表如下:
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
(2)解:从图表可知,共有16种等可能的情况,其中两次所掷数字的和为奇数的情况有8种,和为偶数的有8种,
所以小明获胜的概率为、小刚获胜的概率为,
故此游戏对两人是公平的.
18.(1)这次调查的样本容量为20÷40%=50,
扇形统计图中“绘画”对应扇形的圆心角的大小为360°×(100%-32%-18%-40%)=36°,
故答案为:50;36°;
(2)人;
(3)列表如下:
男1 男2 女1 女2 女3
男1 男1男2 男1女1 男1女2 男1士3
男2 男2男1 男2女 男2女2 男2女3
女l 女1男1 女1男2 女1女2 女1女3
女2 女2男1 女1里2 女2女1 女2女3
女3 女3男1 女3男2 女3女 女3女2
任选2人参加绘画展演共有20种等可能的结果,其中1男1女共有12种,故选中1男1女的概率为:P(1男1女).
同课章节目录
