13.3.2等边三角形同步练习(含答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.3.2等边三角形同步练习(含答案)2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 599.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 17:24:18 | ||
图片预览


文档简介
13.3.2等边三角形 同步练习
2022—2023学年人教版数学八年级 上册(含答案)
一、单选题
1.下列条件不能得到等边三角形的是( )
A.有两个内角是的三角形 B.有一个角是的等腰三角形
C.腰和底相等的等腰三角形 D.有两个角相等的等腰三角形
2.在中,,则的长为( )
A. B. C. D.
3.如图,△ABC中,,,,,则的度数为( )
A. B. C. D.
4.如图,直线、交于点,若、是等边的两条对称轴,且点在直线上(不与点重合),则点、中必有一个在( ).
A.的内部 B.的内部 C.的内部 D.的内部
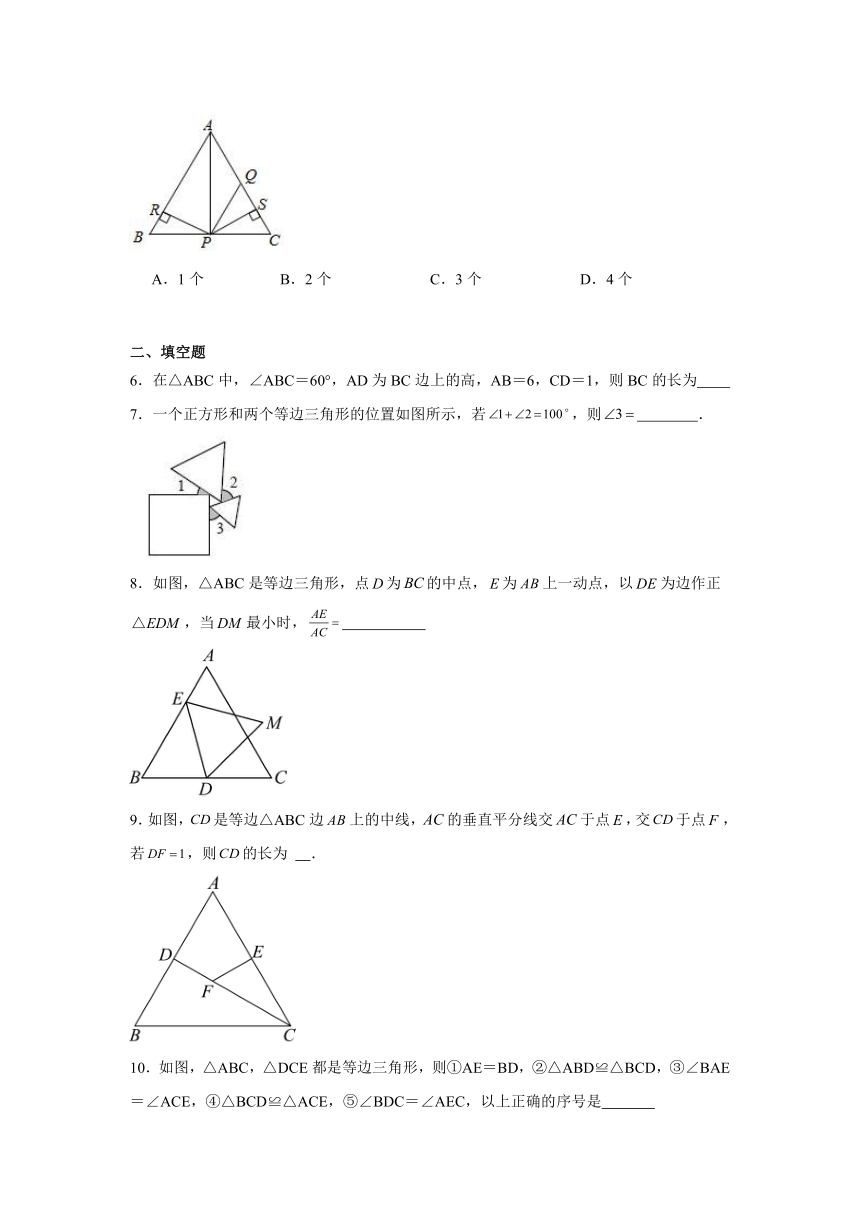
5.如图,△ABC是等边三角形,,于点,于点,点在的平分线上;则下列结论:①,②,③,④△BRP≌△QSP,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.在△ABC中,∠ABC=60°,AD为BC边上的高,AB=6,CD=1,则BC的长为
7.一个正方形和两个等边三角形的位置如图所示,若,则 .
8.如图,△ABC是等边三角形,点为的中点,为上一动点,以为边作正,当最小时,
9.如图,是等边△ABC边上的中线,的垂直平分线交于点,交于点,若,则的长为 .
10.如图,△ABC,△DCE都是等边三角形,则①AE=BD,②△ABD≌△BCD,③∠BAE=∠ACE,④△BCD≌△ACE,⑤∠BDC=∠AEC,以上正确的序号是
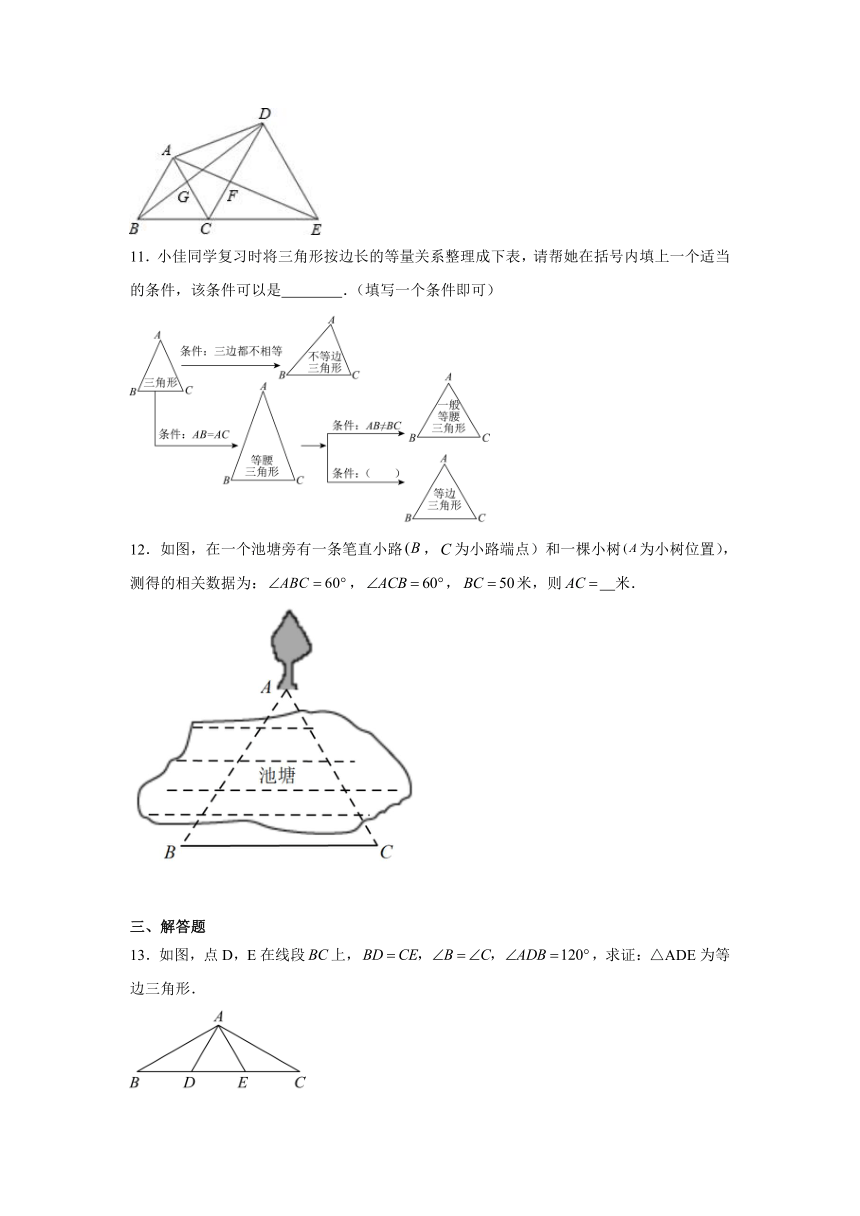
11.小佳同学复习时将三角形按边长的等量关系整理成下表,请帮她在括号内填上一个适当的条件,该条件可以是 .(填写一个条件即可)
12.如图,在一个池塘旁有一条笔直小路,为小路端点)和一棵小树为小树位置),测得的相关数据为:,,米,则 米.
三、解答题
13.如图,点D,E在线段上,,求证:△ADE为等边三角形.
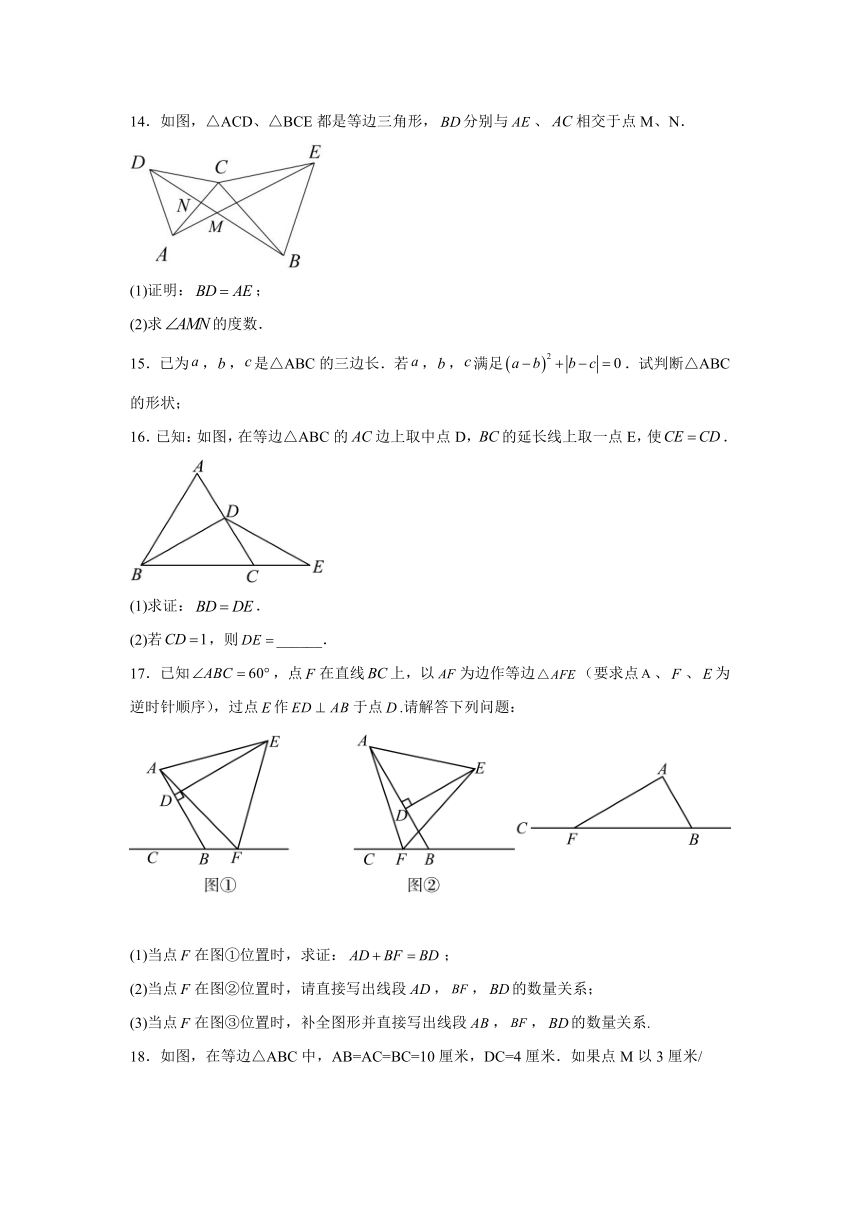
14.如图,△ACD、△BCE都是等边三角形,分别与、相交于点M、N.
(1)证明:;
(2)求的度数.
15.已为,,是△ABC的三边长.若,,满足.试判断△ABC的形状;
16.已知:如图,在等边△ABC的边上取中点D,的延长线上取一点E,使.
(1)求证:.
(2)若,则______.
17.已知,点在直线上,以为边作等边(要求点、、为逆时针顺序),过点作于点.请解答下列问题:
(1)当点在图①位置时,求证:;
(2)当点在图②位置时,请直接写出线段,,的数量关系;
(3)当点在图③位置时,补全图形并直接写出线段,,的数量关系.
18.如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点M以3厘米/
秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.
①经过2秒后,△BMN和△CDM是否全等?请说明理由.
②当两点的运动时间为多少时,△BMN是一个直角三角形?
(2)若点N的运动速度与点M的运动速度不相等,如果△BMN≌△CMD,此时点N的运动速度为多少.
参考答案:
1.D
2.C
3.C
4.D
5.D
6.4
7./50度
8.
9.3
10.①④⑤
11.(答案不唯一)
12.50
13.证明:∵,
∴,
在和中,,
∴,
∴,
∴△ADE为等腰三角形.
∵,
∴,
∴△ADE为等边三角形.
14.(1)证明:∵△ACD、△BCE都是等边三角形,
∴,,
∴,
即,
在和中,
∵,
∴,
∴;
(2)解:∵△ACD是等边三角形,
∴,
∵,
∴,
∴∴.
15.等边三角形
16.(1)证明:D是等边三角形的边上中点,
,,
平分 ,,
,
,
,
又,
,
,
,
(2)由(1)可知:
,
在直角△BDC中,,,
,
,
,
故答案为:.
17.(1)证明:在直线上取一点,使得,连接,如图所示:
∵
∴
∵
∴
∵
∴
即:
∴
∵,
∴
∴
∵
∴
∴
即:
(2)解::
在直线上取一点,使得,连接,如图所示:
∵
∴
∵
∴
∵
∴
即:
∴
∴
∵,
∴△ADE≌△FGE
∴
∵
∴△BDE≌△BGE
∴
即:
(3)解:如图所示:,理由如下:
连接,在上截取,使得,连接
∵,
∴△ABT是等边三角形
∴,
∵
∴
∵
∴△ATF≌△ABE
∴
∴
∴
∴
∵
∴
即:
18.(1)①全等;②t=秒或t=秒;(2)
2022—2023学年人教版数学八年级 上册(含答案)
一、单选题
1.下列条件不能得到等边三角形的是( )
A.有两个内角是的三角形 B.有一个角是的等腰三角形
C.腰和底相等的等腰三角形 D.有两个角相等的等腰三角形
2.在中,,则的长为( )
A. B. C. D.
3.如图,△ABC中,,,,,则的度数为( )
A. B. C. D.
4.如图,直线、交于点,若、是等边的两条对称轴,且点在直线上(不与点重合),则点、中必有一个在( ).
A.的内部 B.的内部 C.的内部 D.的内部
5.如图,△ABC是等边三角形,,于点,于点,点在的平分线上;则下列结论:①,②,③,④△BRP≌△QSP,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.在△ABC中,∠ABC=60°,AD为BC边上的高,AB=6,CD=1,则BC的长为
7.一个正方形和两个等边三角形的位置如图所示,若,则 .
8.如图,△ABC是等边三角形,点为的中点,为上一动点,以为边作正,当最小时,
9.如图,是等边△ABC边上的中线,的垂直平分线交于点,交于点,若,则的长为 .
10.如图,△ABC,△DCE都是等边三角形,则①AE=BD,②△ABD≌△BCD,③∠BAE=∠ACE,④△BCD≌△ACE,⑤∠BDC=∠AEC,以上正确的序号是
11.小佳同学复习时将三角形按边长的等量关系整理成下表,请帮她在括号内填上一个适当的条件,该条件可以是 .(填写一个条件即可)
12.如图,在一个池塘旁有一条笔直小路,为小路端点)和一棵小树为小树位置),测得的相关数据为:,,米,则 米.
三、解答题
13.如图,点D,E在线段上,,求证:△ADE为等边三角形.
14.如图,△ACD、△BCE都是等边三角形,分别与、相交于点M、N.
(1)证明:;
(2)求的度数.
15.已为,,是△ABC的三边长.若,,满足.试判断△ABC的形状;
16.已知:如图,在等边△ABC的边上取中点D,的延长线上取一点E,使.
(1)求证:.
(2)若,则______.
17.已知,点在直线上,以为边作等边(要求点、、为逆时针顺序),过点作于点.请解答下列问题:
(1)当点在图①位置时,求证:;
(2)当点在图②位置时,请直接写出线段,,的数量关系;
(3)当点在图③位置时,补全图形并直接写出线段,,的数量关系.
18.如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点M以3厘米/
秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.
①经过2秒后,△BMN和△CDM是否全等?请说明理由.
②当两点的运动时间为多少时,△BMN是一个直角三角形?
(2)若点N的运动速度与点M的运动速度不相等,如果△BMN≌△CMD,此时点N的运动速度为多少.
参考答案:
1.D
2.C
3.C
4.D
5.D
6.4
7./50度
8.
9.3
10.①④⑤
11.(答案不唯一)
12.50
13.证明:∵,
∴,
在和中,,
∴,
∴,
∴△ADE为等腰三角形.
∵,
∴,
∴△ADE为等边三角形.
14.(1)证明:∵△ACD、△BCE都是等边三角形,
∴,,
∴,
即,
在和中,
∵,
∴,
∴;
(2)解:∵△ACD是等边三角形,
∴,
∵,
∴,
∴∴.
15.等边三角形
16.(1)证明:D是等边三角形的边上中点,
,,
平分 ,,
,
,
,
又,
,
,
,
(2)由(1)可知:
,
在直角△BDC中,,,
,
,
,
故答案为:.
17.(1)证明:在直线上取一点,使得,连接,如图所示:
∵
∴
∵
∴
∵
∴
即:
∴
∵,
∴
∴
∵
∴
∴
即:
(2)解::
在直线上取一点,使得,连接,如图所示:
∵
∴
∵
∴
∵
∴
即:
∴
∴
∵,
∴△ADE≌△FGE
∴
∵
∴△BDE≌△BGE
∴
即:
(3)解:如图所示:,理由如下:
连接,在上截取,使得,连接
∵,
∴△ABT是等边三角形
∴,
∵
∴
∵
∴△ATF≌△ABE
∴
∴
∴
∴
∵
∴
即:
18.(1)①全等;②t=秒或t=秒;(2)
