11.3.2《多边形及其内角和》 优质课件(共30张PPT) 人教版数学八年级上册
文档属性
| 名称 | 11.3.2《多边形及其内角和》 优质课件(共30张PPT) 人教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 164.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 17:31:39 | ||
图片预览





文档简介
(共30张PPT)
人教版八年级数学上册第十一章第三节 多边形及其内角和
教学目标
1、通过实验探究,归纳出多边形内角和公式;运用多边形的内角和公式解决简单问题。
2、经历测量、类比、归纳等活动,感受数学思考过程的条理性,发展合情推理能力和语言表达能力;通过把多边形转化成三角形,体会转化思想在几何中的应用,同时体会从特殊到一般的认识问题的方法;体会几何“实验”与“论证”的两个方面,逐步从实验几何向论证几何过渡。
3、培养数学抽象、直观想象的学科核心素养。
教学重点:
探索多边形内角和公式
探索多边形内角和时,如何把多边形转化为三角形
教学难点:
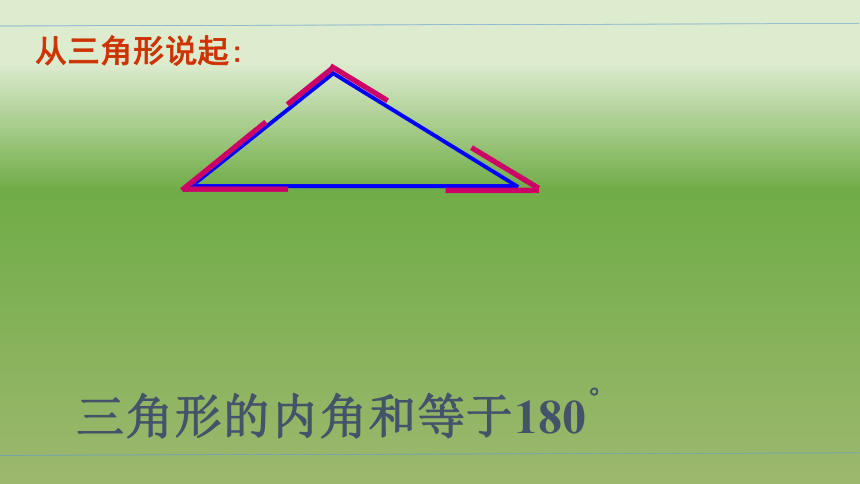
三角形的内角和等于180°
从三角形说起:
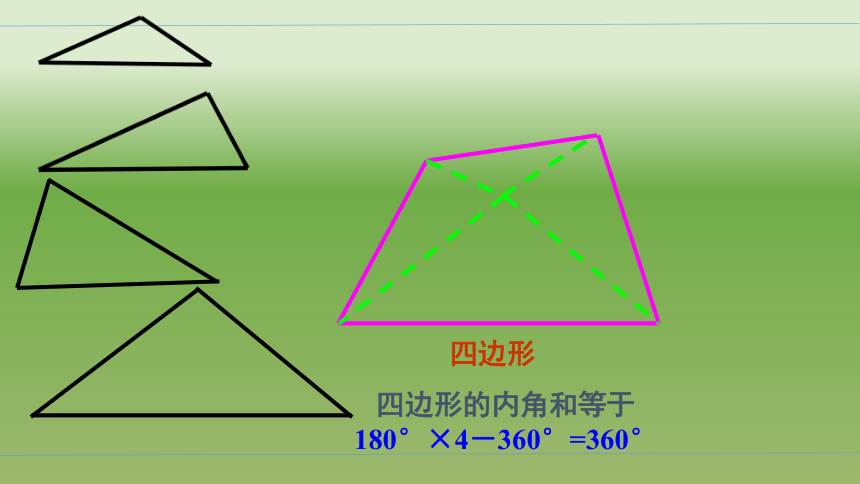
活动1:探索四边形的内角和
问题1:给你一个三角形,你至少要增添几条线段才能把它变成四边形?
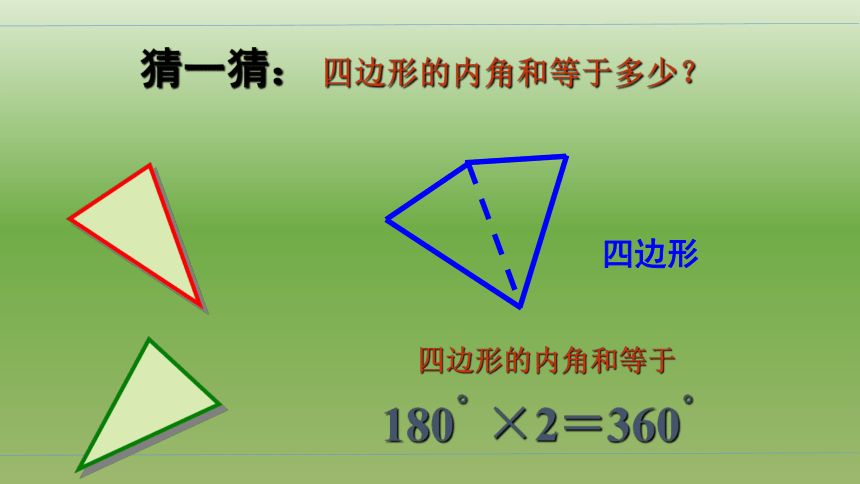
四边形
四边形的内角和等于
180°×2=360°
猜一猜: 四边形的内角和等于多少?
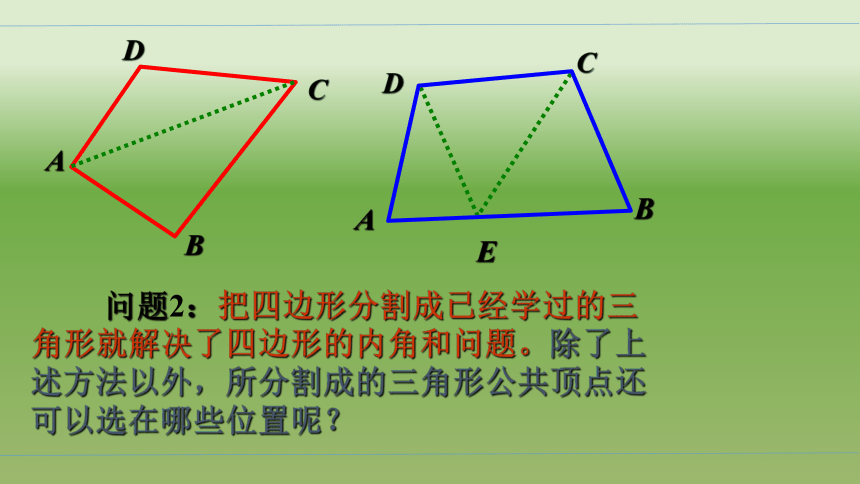
问题2:把四边形分割成已经学过的三角形就解决了四边形的内角和问题。除了上述方法以外,所分割成的三角形公共顶点还可以选在哪些位置呢?
C
A
B
D
A
B
C
D
E
D
A
B
C
四边形的内角和等于
180°×4-360°=360°
四边形
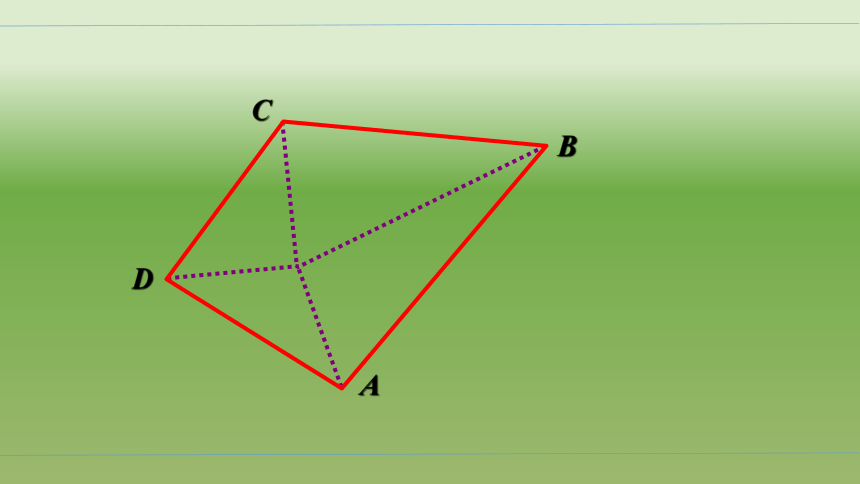
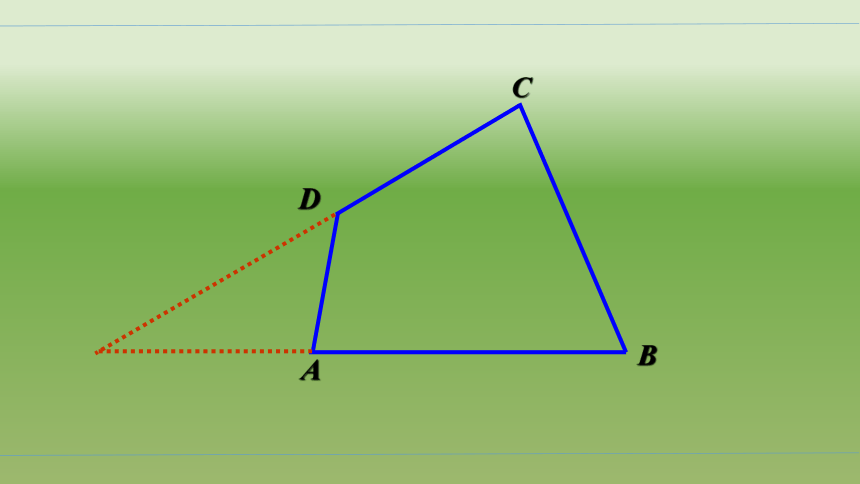
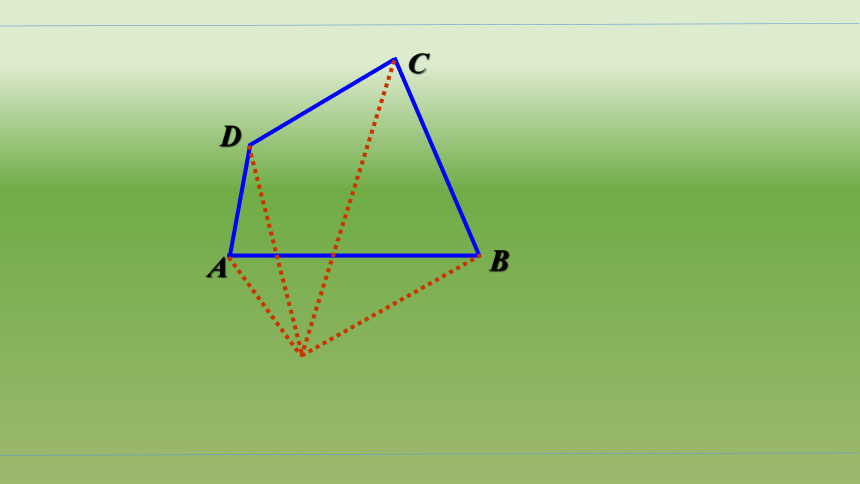
问题3:如果我们把“分割点” 取在四边形外,你还能不能找到类似的办法解决四边形的内角和问题?
A
B
C
D
A
B
C
D
问题4:给你一个四边形,你至少要增添几条线段才能把它变成五边形?
活动1:探索四边形的内角和
活动2:探索五边形的内角和
问题5:再给一个五边形,你怎样求它的内角和?
B
C
D
E
A
五边形内角和等于
180°×3=540°
B
C
E
A
D
活动1:探索四边形的内角和
活动2:探索五边形的内角和
活动3:探索任意多边形的内角和
问题6:不同的多边形,它的内角和也不同。你们知道多边形内角和是随着哪个量变化而变化的吗?
多边形 边数 图形 分成三角形的个数 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
3
4
5
6
7
n
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
n 边形的内角和公式:
活动1:探索四边形的内角和
活动2:探索五边形的内角和
活动3:探索任意多边形的内角和
活动4:多边形内角和公式的运用
【例题】如果一个四边形的一组对角互补,那么另一组对角有什么关系?
强化练习,互问游戏
规则:同学说出多边形的边数,由同桌求和;说出度数求边数。(利用教学助手随机点名,三组即可)
右图是三个完全相同的正多边形拼成的地板(无缝隙、不重叠的图形)的一部分,这种多边形是几边形?为什么?
放飞思想
延伸与拓展
小丽想:今年是2017年,设计一个内角和为2 017°的多边形图案特别有趣。你认为小丽的想法可行吗?
活动1:探索四边形的内角和
活动2:探索五边形的内角和
活动3:探索任意多边形的内角和
活动4:多边形内角和公式的运用
活动5:小结、布置作业
注意:分割出来的三角形必须不重不漏
B
C
E
A
D
F
G
“波浪线”法
这节课你有什么收获?
这节课你还有什么困惑?
1.我们得到了多边形的内角和公式;
2.求多边形的内角和,我们可以将它转化为三角形来解决,从中体会到了转化的思想;
3.我们先解决了四边形的内角和问题,运用类比、猜想论证的方法进而解决了五边形乃至 n 边形的内角和问题,从中体会到了由特殊到一般的思想。
通过本节课我知道了……我能……需要注意的是……我感悟了....数学思想
总结反思,形成数学情感体验
作业
1、课本第24页练习1、2、3.
2、设计多边形拼图游戏。
人教版八年级数学上册第十一章第三节 多边形及其内角和
教学目标
1、通过实验探究,归纳出多边形内角和公式;运用多边形的内角和公式解决简单问题。
2、经历测量、类比、归纳等活动,感受数学思考过程的条理性,发展合情推理能力和语言表达能力;通过把多边形转化成三角形,体会转化思想在几何中的应用,同时体会从特殊到一般的认识问题的方法;体会几何“实验”与“论证”的两个方面,逐步从实验几何向论证几何过渡。
3、培养数学抽象、直观想象的学科核心素养。
教学重点:
探索多边形内角和公式
探索多边形内角和时,如何把多边形转化为三角形
教学难点:
三角形的内角和等于180°
从三角形说起:
活动1:探索四边形的内角和
问题1:给你一个三角形,你至少要增添几条线段才能把它变成四边形?
四边形
四边形的内角和等于
180°×2=360°
猜一猜: 四边形的内角和等于多少?
问题2:把四边形分割成已经学过的三角形就解决了四边形的内角和问题。除了上述方法以外,所分割成的三角形公共顶点还可以选在哪些位置呢?
C
A
B
D
A
B
C
D
E
D
A
B
C
四边形的内角和等于
180°×4-360°=360°
四边形
问题3:如果我们把“分割点” 取在四边形外,你还能不能找到类似的办法解决四边形的内角和问题?
A
B
C
D
A
B
C
D
问题4:给你一个四边形,你至少要增添几条线段才能把它变成五边形?
活动1:探索四边形的内角和
活动2:探索五边形的内角和
问题5:再给一个五边形,你怎样求它的内角和?
B
C
D
E
A
五边形内角和等于
180°×3=540°
B
C
E
A
D
活动1:探索四边形的内角和
活动2:探索五边形的内角和
活动3:探索任意多边形的内角和
问题6:不同的多边形,它的内角和也不同。你们知道多边形内角和是随着哪个量变化而变化的吗?
多边形 边数 图形 分成三角形的个数 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
3
4
5
6
7
n
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
n 边形的内角和公式:
活动1:探索四边形的内角和
活动2:探索五边形的内角和
活动3:探索任意多边形的内角和
活动4:多边形内角和公式的运用
【例题】如果一个四边形的一组对角互补,那么另一组对角有什么关系?
强化练习,互问游戏
规则:同学说出多边形的边数,由同桌求和;说出度数求边数。(利用教学助手随机点名,三组即可)
右图是三个完全相同的正多边形拼成的地板(无缝隙、不重叠的图形)的一部分,这种多边形是几边形?为什么?
放飞思想
延伸与拓展
小丽想:今年是2017年,设计一个内角和为2 017°的多边形图案特别有趣。你认为小丽的想法可行吗?
活动1:探索四边形的内角和
活动2:探索五边形的内角和
活动3:探索任意多边形的内角和
活动4:多边形内角和公式的运用
活动5:小结、布置作业
注意:分割出来的三角形必须不重不漏
B
C
E
A
D
F
G
“波浪线”法
这节课你有什么收获?
这节课你还有什么困惑?
1.我们得到了多边形的内角和公式;
2.求多边形的内角和,我们可以将它转化为三角形来解决,从中体会到了转化的思想;
3.我们先解决了四边形的内角和问题,运用类比、猜想论证的方法进而解决了五边形乃至 n 边形的内角和问题,从中体会到了由特殊到一般的思想。
通过本节课我知道了……我能……需要注意的是……我感悟了....数学思想
总结反思,形成数学情感体验
作业
1、课本第24页练习1、2、3.
2、设计多边形拼图游戏。
