人教版七年级下册数学 第7章 小结 教案
文档属性
| 名称 | 人教版七年级下册数学 第7章 小结 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 207.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 20:18:39 | ||
图片预览


文档简介
人教版 数学 七年级下册第七章 平面直角坐标系
与三角形面积有关的 多结论问题一
教学目标:1、结合平面直角坐标系中,点坐标的含义,解决简单的面积问题。
2、在计算和画图中探寻与三角形面积有关的几何模型;
提高学生分类讨论和总结归纳的能力。
3、尝试用总结的几何模型,构造满足条件的图形;
提高学生实际操作的能力。
教学重点:1、提高学生数学建模的思想。
2、逐步消除学生画图中的“盲区”,增强学生画图时的分类意识。
教学难点:从特殊图形中提炼出与之有关的几何模型。
教学方法:讲练结合法。
教学过程:
回顾旧知:
回顾小学学习的三角形面积的计算方法。
说出以下三角形的面积公式:
引入新课:
在平面直角坐标系中,ΔABC的面积为2,点A(0,0)、点B(1,2)、
点C在坐标轴上。请画出所有满足条件的ΔABC,并求出点C的坐标。
分析:1、点C在坐标轴上,需要分点C在x轴、y轴两种情况画图。
2、思考:点C在线段AB的哪一侧呢?
3、男、女生分别就点C在x轴、y轴两种情况画图计算。(学生代表演板)
4、观察分类后的两个图形,思考:(图三)当AO与BC满足什么位置关系时,ΔAOB的面积等于ΔAOC的面积?
抽丝剥茧
几何画板演示:在拖动点A时,对比测量的ΔAOB和ΔAOC的面积。
利用三角形面积公式,计算两个三角形的面积。
探究归纳 几何模型一:
4、四个ΔABC合在一个坐标系上,选取线段AB同侧的两个三角形,连接C2C3,观察 C2C3与AB的位置关系。
5、几何画板演示:在拖动线段AB时,对比测量的ΔABC和ΔABD的面积。
6、探究归纳 几何模型二:
学以致用:
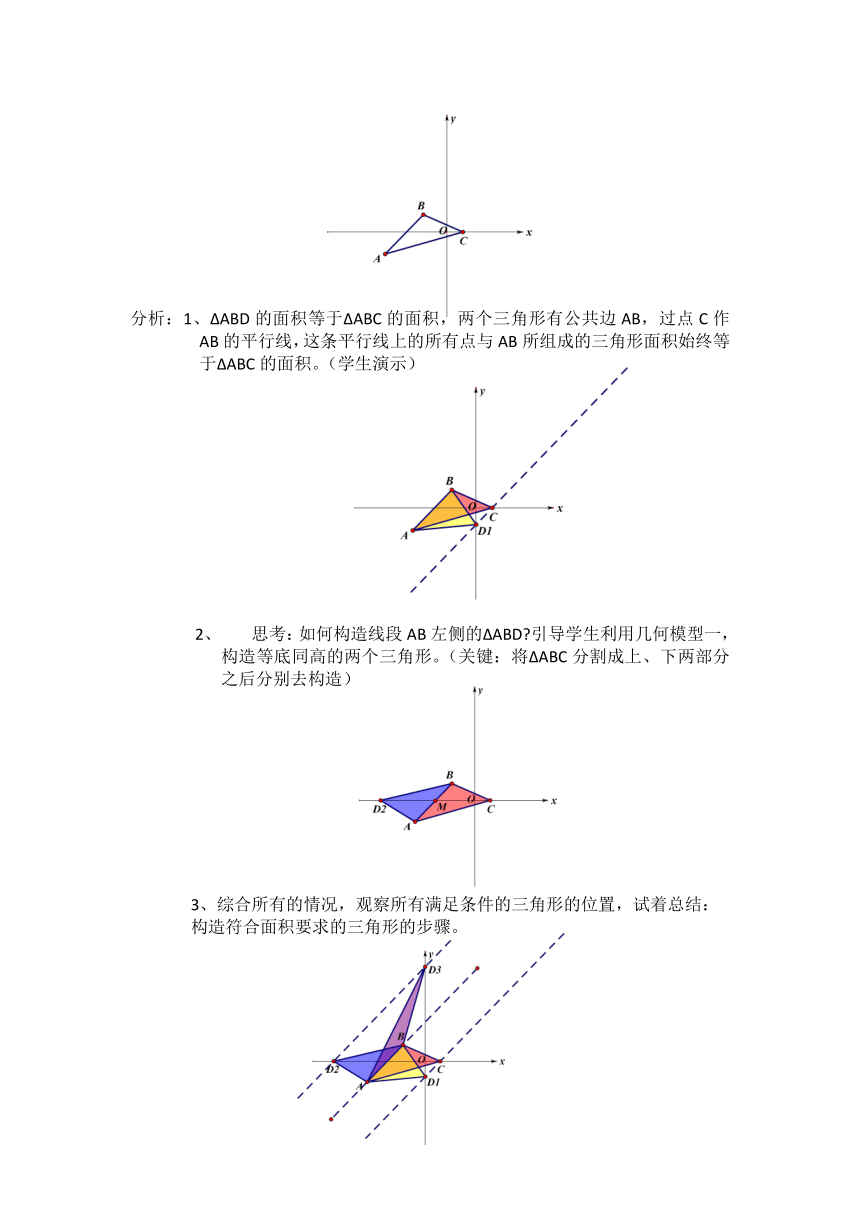
例二:在平面直角坐标系中,ΔABC的形状和位置如图所示,点C在x轴上,点D在坐标轴上,并且ΔABD的面积等于ΔABC的面积,你能画出所有满足条件的ΔABD吗?你能试着总结:将所有点D找全的方法吗?
分析:1、ΔABD的面积等于ΔABC的面积,两个三角形有公共边AB,过点C作AB的平行线,这条平行线上的所有点与AB所组成的三角形面积始终等于ΔABC的面积。(学生演示)
思考:如何构造线段AB左侧的ΔABD 引导学生利用几何模型一,构造等底同高的两个三角形。(关键:将ΔABC分割成上、下两部分之后分别去构造)
3、综合所有的情况,观察所有满足条件的三角形的位置,试着总结:
构造符合面积要求的三角形的步骤。
再接再厉:
练习:在平面直角坐标系中有一个6×5的小正方形网格(如图所示),格点
A(1,1)、格点B(2,2)。请你在此网格中,找到格点C,使ΔABC的面积为1个平方单位;你能画出所有满足条件的ΔABC吗?看看图中暗藏几种模型?
分析:1、分线段AB的左右两侧,选择符合面积要求的两个点C;
2、过点C作线段AB的两条平行线,这两条平行线与网格的交点即为所求的点 C
3分类连接三角形,观察暗藏其中的几何模型。
归纳小结:
1、这节课中我们得到的与三角形面积有关的几何模型:
(几何模型一)
(几何模型二)
2、在平面直角坐标系中满足面积要求的三角形通常有多个,如何构造,才能不漏掉任何一个?说出你总结的步骤。
3、这节课我们主要解决了多结论问题中画图的方法,如何计算满足面积要求的三角形第三个顶点的坐标呢?下节课我们重点解决:计算第三点的坐标问题,有兴趣的学生可以在课后练习中,试着探究点坐标的计算方法,能否像这节课一样,总结出有推广价值的计算步骤呢?欢迎课后同学们和我交流你们的新发现!
七、课后作业:
1、(学生二选一)
A组基础篇 《与三角形面积有关的多结论问题 练习一》
B组提高篇 《与三角形面积有关的多结论问题 练习二》
课外探究:
探究三角形面积 几何模型二 :
深层次的探究:在AB∕∕CD的条件下,图中共有几组面积相等的三角形?如何说理?
探究三角形面积 几何模型三:
深层次的探究:当例二中的ΔABC不具备任何特殊位置时,图中的第二条平行线如何确定位置?在拖动线段AB时,观察黄色、绿色三角形面积相等的条件?如何说理?
三角形的面积 模型三:
欢迎课后同学们与我交流你的收获!
与三角形面积有关的 多结论问题一
教学目标:1、结合平面直角坐标系中,点坐标的含义,解决简单的面积问题。
2、在计算和画图中探寻与三角形面积有关的几何模型;
提高学生分类讨论和总结归纳的能力。
3、尝试用总结的几何模型,构造满足条件的图形;
提高学生实际操作的能力。
教学重点:1、提高学生数学建模的思想。
2、逐步消除学生画图中的“盲区”,增强学生画图时的分类意识。
教学难点:从特殊图形中提炼出与之有关的几何模型。
教学方法:讲练结合法。
教学过程:
回顾旧知:
回顾小学学习的三角形面积的计算方法。
说出以下三角形的面积公式:
引入新课:
在平面直角坐标系中,ΔABC的面积为2,点A(0,0)、点B(1,2)、
点C在坐标轴上。请画出所有满足条件的ΔABC,并求出点C的坐标。
分析:1、点C在坐标轴上,需要分点C在x轴、y轴两种情况画图。
2、思考:点C在线段AB的哪一侧呢?
3、男、女生分别就点C在x轴、y轴两种情况画图计算。(学生代表演板)
4、观察分类后的两个图形,思考:(图三)当AO与BC满足什么位置关系时,ΔAOB的面积等于ΔAOC的面积?
抽丝剥茧
几何画板演示:在拖动点A时,对比测量的ΔAOB和ΔAOC的面积。
利用三角形面积公式,计算两个三角形的面积。
探究归纳 几何模型一:
4、四个ΔABC合在一个坐标系上,选取线段AB同侧的两个三角形,连接C2C3,观察 C2C3与AB的位置关系。
5、几何画板演示:在拖动线段AB时,对比测量的ΔABC和ΔABD的面积。
6、探究归纳 几何模型二:
学以致用:
例二:在平面直角坐标系中,ΔABC的形状和位置如图所示,点C在x轴上,点D在坐标轴上,并且ΔABD的面积等于ΔABC的面积,你能画出所有满足条件的ΔABD吗?你能试着总结:将所有点D找全的方法吗?
分析:1、ΔABD的面积等于ΔABC的面积,两个三角形有公共边AB,过点C作AB的平行线,这条平行线上的所有点与AB所组成的三角形面积始终等于ΔABC的面积。(学生演示)
思考:如何构造线段AB左侧的ΔABD 引导学生利用几何模型一,构造等底同高的两个三角形。(关键:将ΔABC分割成上、下两部分之后分别去构造)
3、综合所有的情况,观察所有满足条件的三角形的位置,试着总结:
构造符合面积要求的三角形的步骤。
再接再厉:
练习:在平面直角坐标系中有一个6×5的小正方形网格(如图所示),格点
A(1,1)、格点B(2,2)。请你在此网格中,找到格点C,使ΔABC的面积为1个平方单位;你能画出所有满足条件的ΔABC吗?看看图中暗藏几种模型?
分析:1、分线段AB的左右两侧,选择符合面积要求的两个点C;
2、过点C作线段AB的两条平行线,这两条平行线与网格的交点即为所求的点 C
3分类连接三角形,观察暗藏其中的几何模型。
归纳小结:
1、这节课中我们得到的与三角形面积有关的几何模型:
(几何模型一)
(几何模型二)
2、在平面直角坐标系中满足面积要求的三角形通常有多个,如何构造,才能不漏掉任何一个?说出你总结的步骤。
3、这节课我们主要解决了多结论问题中画图的方法,如何计算满足面积要求的三角形第三个顶点的坐标呢?下节课我们重点解决:计算第三点的坐标问题,有兴趣的学生可以在课后练习中,试着探究点坐标的计算方法,能否像这节课一样,总结出有推广价值的计算步骤呢?欢迎课后同学们和我交流你们的新发现!
七、课后作业:
1、(学生二选一)
A组基础篇 《与三角形面积有关的多结论问题 练习一》
B组提高篇 《与三角形面积有关的多结论问题 练习二》
课外探究:
探究三角形面积 几何模型二 :
深层次的探究:在AB∕∕CD的条件下,图中共有几组面积相等的三角形?如何说理?
探究三角形面积 几何模型三:
深层次的探究:当例二中的ΔABC不具备任何特殊位置时,图中的第二条平行线如何确定位置?在拖动线段AB时,观察黄色、绿色三角形面积相等的条件?如何说理?
三角形的面积 模型三:
欢迎课后同学们与我交流你的收获!
