4.1 平方根(第1课时) 课件(共28张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 4.1 平方根(第1课时) 课件(共28张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 19:30:02 | ||
图片预览







文档简介
(共28张PPT)
第4章 · 平方根
4.1 平方根(1)
第1课时 平方根
学习目标
1. 了解平方根的概念,会用符号正确地表示非负数的平方根;
2. 了解开平方运算和平方运算之间的互逆关系,会求某些非负数的平方根,发展逆向思维.
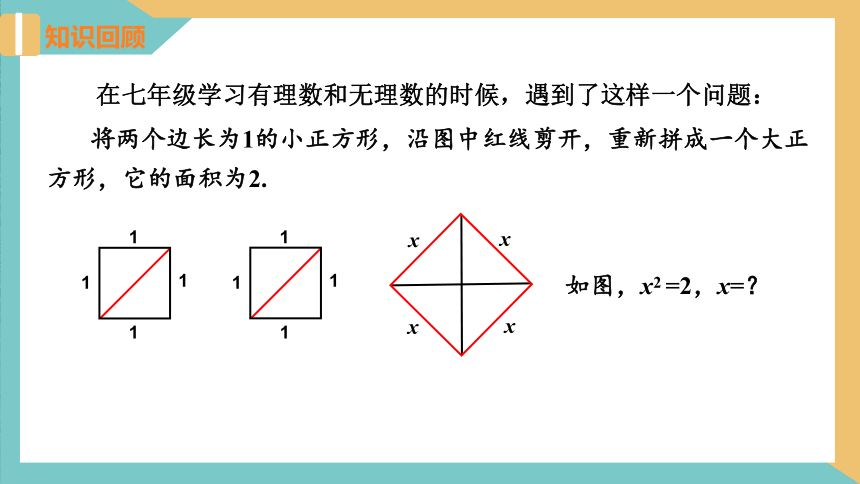
知识回顾
将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.
在七年级学习有理数和无理数的时候,遇到了这样一个问题:
如图,x2 =2,x=?
1
1
1
1
x
x
x
x
1
1
1
1
问题引入
如图,设图中小方格的边长为1,你能算出图中AB、A′B′的长吗?
A
B
C
A′
B′
C′
问题引入
A
B
C
A′
B′
C′
在Rt△ABC中,A B2=32+42=25,
∴AB=5.
在Rt△A′B′C′中,A′B′2=42+52=41,
∴A′B′=
就是研究当x2=a时,x是什么数?
要解决上面问题,
±2
当x2=4时,
∵ 22=4, (-2)2=4,
∴ x=
∵(±2)2= 4,
讨论与交流
当x2=时,
∵ = ,=,
±
∴ x=
∵(±)2= ,
当x2=0.25时,
∵ 0.52=0.25,(-0.5)2=0.25,
∴ x=
±0.5
问题1:观察上面各式,等号右边的数都什么数?
∵ (±0.5)2=0.25,
问题2:使x2=a(a>0)成立的数x有几个?它们之间有什么关系?
正数
有两个,它们互为相反数.
讨论与交流
问题3:当a=0时, x2 =a成立吗?如果成立,x=?
问题4:当a<0时, x2 =a成立吗?
成立,x=0.
不成立.
概念学习
如果x2=a (a≥0),那么x叫做a的平方根,也称为二次方根.
平方根的定义:
22=4
____是4的平方根
2
(-2)2=4
____是4的平方根
-2
(±2)2=4
____是4的平方根
±2
4的平方根是±2
0.52=0.25
____是0.25的平方根
0.5
(-0.5)2=0.25
_____是0.25的平方根
-0.5
(±0.5)2=0.25
_____是0.25的平方根
±0.5
0.25的平方根是±0.5
2的平方根是多少呢?
概念学习
符号表示:
读作:
根号
2的正的平方根是______,读作__________;
根号2
2的负的平方根是______,读作__________;
-
负根号2
2的平方根是______,读作_______________.
±
正、负根号2
概念学习
符号表示:
读作:
根号
读作 ____________;
正数a的正的平方根记作______,
根号a
正数a的负的平方根记作______,
-
读作 ____________;
负根号a
正数a的两个平方根记作______,
±
读作 ______________.
正、负根号a
新知应用
填空:
⑴ 3的平方根是_______;
⑵ 3.5的正的平方根是__________;
⑶ 1的负的平方根是___________;
⑷表示:___________________________;
⑸表示:_______________________________;
⑹表示:____________________________.
±
-
20的负的平方根
13的平方根
19的正的平方根
新知应用
上面的问题中,
如图,x2 =2,x=?
x
x
x
x
A′
B′
C′
A′B′2=42+52=41,A′B′=
例题讲解
例1 求下列各数的平方根:
(1)25 (2) (3)15 (4)0.09 (5)1
解:
(1)∵(±5)2=25,∴25的平方根是±5,即±=±5;
(2)∵(±)2=,∴ 的平方根是±,即±=±;
(3)15的平方根是±;
(4)∵(±0.3)2=0.09,∴ 0.09的平方根是±0.3,即±=±0.3;
(5)∵(±)2=,∴ 1的平方根是±,即±==±.
①正数有两个平方根,±不能丢;
②求平方根时,结果能化简的
一般要化成最简结果;
③带分数要先化为假分数;
再求平方根.
概念学习
定义:求一个数的平方根的运算叫做开平方.
开平方与平方互为逆运算,所以可以通过平方运算来求一个数的平方根.
x2 = a
x
平方
a
开平方
平方根
幂
a
x
检验x是不是a的平方根,只要看x2是不是等于a即可.
开平方
平方根
开平方与平方根对比:
与加、减、乘、除、乘方一样,是一种运算.
只有非负数才能进行开平方运算.
平方根是数,是开平方的结果.
概念学习
新知巩固
a
x
0.1
5
0.01
-7
7
49
-0.1
x2=a
x
求平方
a
?
一个数的一个平方根是7,那么它的另一个平方根是________,这个数是__________.
-7
49
a
x
-
下列各数有平方根吗?如果有,请写出来;如果没有,请说明理由.
, , , , , , .
9
5
0
-8
-36
新知巩固
解:9,5,,0有平方根;,-8,-36没有平方根.
9的平方根是±=±3;
5的平方根是±;
的平方根是±=±;
0的平方根是0.
判断一个数有无平方根, 就看这个数是否为非负数.
新知归纳
一个正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
平方根的性质:
新知巩固
1.下列各数有平方根吗?如果有,求出它的平方根.
17, 0, -16, (-5)2, , -(-23)
解:17,0,(-5)2,-(-23)有平方根;-16,没有平方根.
17的平方根是±;
0的平方根是0;
(-5)2的平方根是±=±5;
-(-23)的平方根是±.
新知巩固
2.判断下列说法是否正确:
① -5是25的平方根( ) ②25的平方根是-5 ( )
③0的平方根是0 ( ) ④只有正数有平方根( )
⑤ (-3)2的平方根是-3( )⑥3平方的平方根是3( )
⑦-a没有平方根 ( ) ⑧把一个数先平方再开平方得原数( )
×
×
√
√
×
×
×
×
3.求下列各式中x的值:
(1)x2=16; (2)5x2-4=11; (3)(x-1)2=9.
由题可知x-1=±3,∴x=4或x=-2.
移项,得5x2=15,系数化为1,得x2=3,∴x=±.
解:
x=±,
x=±4.
新知巩固
拓展延伸
一个正数的两个平方根为2x-1与5x-13,求x的值和这个数.
解:根据题意得:(2x-1)+(5x-13)=0
2x-1+5x-13 =0
2x+5x =1+13
7x =14
x =2
∵ 当x=2时,2x-1=2×2-1=4-1=3,∴ 32=9
或者 ∵ 当x=-2时, 5x-13=5×2-13=10-13=-3,∴ (-3)2=9
答:x的值为2,这个数为9.
课堂小结
平方根
概念与表示方法
平方根的性质
开平方
当堂检测
1. 4的平方根是( )A. B. 2 C. -2 D. ±2
D
2. (-0.6)2的平方根是( )A. -0.6 B. 0.6 C. ±0.6 D. 0.36
C
当堂检测
3. 的平方根是±,用数学式子表示为( )A. =± B.= C.±=± D.±=±
C
当堂检测
4.如果-b是a的平方根,那么( )A. b=a2 B. a=b2 C. b=-a2 D. a=-b2
B
5.下列有关平方根的叙述,正确的个数是( )①如果a存在平方根,那么a>0;②如果a有两个不相等的平方根,那么a>0;③如果a没有平方根,那么a<0;④如果a>0,那么a的平方根也大于0.A.1 B.2 C.3 D.4
B
当堂检测
6.若一个数的平方等于2,则这个数等于________.
±
7.若3x+2有平方根,则x的取值范围为_________.
x≥-
8.一个正数的两个不同的平方根分别是a-1和5-2a,则这个正数是_____.
9
10.写出下列各数的平方根:
81,289,0,2 ,2.56,0.81,(-2)4
当堂检测
(1) 4x2=81; (2)5x2-10=0; (3) (x-1)2=36.
11.求下列各式中x的值:
第4章 · 平方根
4.1 平方根(1)
第1课时 平方根
学习目标
1. 了解平方根的概念,会用符号正确地表示非负数的平方根;
2. 了解开平方运算和平方运算之间的互逆关系,会求某些非负数的平方根,发展逆向思维.
知识回顾
将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.
在七年级学习有理数和无理数的时候,遇到了这样一个问题:
如图,x2 =2,x=?
1
1
1
1
x
x
x
x
1
1
1
1
问题引入
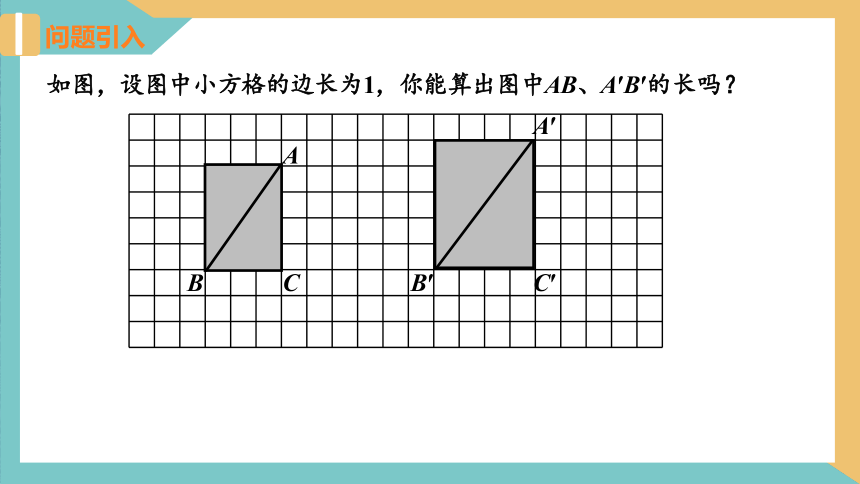
如图,设图中小方格的边长为1,你能算出图中AB、A′B′的长吗?
A
B
C
A′
B′
C′
问题引入
A
B
C
A′
B′
C′
在Rt△ABC中,A B2=32+42=25,
∴AB=5.
在Rt△A′B′C′中,A′B′2=42+52=41,
∴A′B′=
就是研究当x2=a时,x是什么数?
要解决上面问题,
±2
当x2=4时,
∵ 22=4, (-2)2=4,
∴ x=
∵(±2)2= 4,
讨论与交流
当x2=时,
∵ = ,=,
±
∴ x=
∵(±)2= ,
当x2=0.25时,
∵ 0.52=0.25,(-0.5)2=0.25,
∴ x=
±0.5
问题1:观察上面各式,等号右边的数都什么数?
∵ (±0.5)2=0.25,
问题2:使x2=a(a>0)成立的数x有几个?它们之间有什么关系?
正数
有两个,它们互为相反数.
讨论与交流
问题3:当a=0时, x2 =a成立吗?如果成立,x=?
问题4:当a<0时, x2 =a成立吗?
成立,x=0.
不成立.
概念学习
如果x2=a (a≥0),那么x叫做a的平方根,也称为二次方根.
平方根的定义:
22=4
____是4的平方根
2
(-2)2=4
____是4的平方根
-2
(±2)2=4
____是4的平方根
±2
4的平方根是±2
0.52=0.25
____是0.25的平方根
0.5
(-0.5)2=0.25
_____是0.25的平方根
-0.5
(±0.5)2=0.25
_____是0.25的平方根
±0.5
0.25的平方根是±0.5
2的平方根是多少呢?
概念学习
符号表示:
读作:
根号
2的正的平方根是______,读作__________;
根号2
2的负的平方根是______,读作__________;
-
负根号2
2的平方根是______,读作_______________.
±
正、负根号2
概念学习
符号表示:
读作:
根号
读作 ____________;
正数a的正的平方根记作______,
根号a
正数a的负的平方根记作______,
-
读作 ____________;
负根号a
正数a的两个平方根记作______,
±
读作 ______________.
正、负根号a
新知应用
填空:
⑴ 3的平方根是_______;
⑵ 3.5的正的平方根是__________;
⑶ 1的负的平方根是___________;
⑷表示:___________________________;
⑸表示:_______________________________;
⑹表示:____________________________.
±
-
20的负的平方根
13的平方根
19的正的平方根
新知应用
上面的问题中,
如图,x2 =2,x=?
x
x
x
x
A′
B′
C′
A′B′2=42+52=41,A′B′=
例题讲解
例1 求下列各数的平方根:
(1)25 (2) (3)15 (4)0.09 (5)1
解:
(1)∵(±5)2=25,∴25的平方根是±5,即±=±5;
(2)∵(±)2=,∴ 的平方根是±,即±=±;
(3)15的平方根是±;
(4)∵(±0.3)2=0.09,∴ 0.09的平方根是±0.3,即±=±0.3;
(5)∵(±)2=,∴ 1的平方根是±,即±==±.
①正数有两个平方根,±不能丢;
②求平方根时,结果能化简的
一般要化成最简结果;
③带分数要先化为假分数;
再求平方根.
概念学习
定义:求一个数的平方根的运算叫做开平方.
开平方与平方互为逆运算,所以可以通过平方运算来求一个数的平方根.
x2 = a
x
平方
a
开平方
平方根
幂
a
x
检验x是不是a的平方根,只要看x2是不是等于a即可.
开平方
平方根
开平方与平方根对比:
与加、减、乘、除、乘方一样,是一种运算.
只有非负数才能进行开平方运算.
平方根是数,是开平方的结果.
概念学习
新知巩固
a
x
0.1
5
0.01
-7
7
49
-0.1
x2=a
x
求平方
a
?
一个数的一个平方根是7,那么它的另一个平方根是________,这个数是__________.
-7
49
a
x
-
下列各数有平方根吗?如果有,请写出来;如果没有,请说明理由.
, , , , , , .
9
5
0
-8
-36
新知巩固
解:9,5,,0有平方根;,-8,-36没有平方根.
9的平方根是±=±3;
5的平方根是±;
的平方根是±=±;
0的平方根是0.
判断一个数有无平方根, 就看这个数是否为非负数.
新知归纳
一个正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
平方根的性质:
新知巩固
1.下列各数有平方根吗?如果有,求出它的平方根.
17, 0, -16, (-5)2, , -(-23)
解:17,0,(-5)2,-(-23)有平方根;-16,没有平方根.
17的平方根是±;
0的平方根是0;
(-5)2的平方根是±=±5;
-(-23)的平方根是±.
新知巩固
2.判断下列说法是否正确:
① -5是25的平方根( ) ②25的平方根是-5 ( )
③0的平方根是0 ( ) ④只有正数有平方根( )
⑤ (-3)2的平方根是-3( )⑥3平方的平方根是3( )
⑦-a没有平方根 ( ) ⑧把一个数先平方再开平方得原数( )
×
×
√
√
×
×
×
×
3.求下列各式中x的值:
(1)x2=16; (2)5x2-4=11; (3)(x-1)2=9.
由题可知x-1=±3,∴x=4或x=-2.
移项,得5x2=15,系数化为1,得x2=3,∴x=±.
解:
x=±,
x=±4.
新知巩固
拓展延伸
一个正数的两个平方根为2x-1与5x-13,求x的值和这个数.
解:根据题意得:(2x-1)+(5x-13)=0
2x-1+5x-13 =0
2x+5x =1+13
7x =14
x =2
∵ 当x=2时,2x-1=2×2-1=4-1=3,∴ 32=9
或者 ∵ 当x=-2时, 5x-13=5×2-13=10-13=-3,∴ (-3)2=9
答:x的值为2,这个数为9.
课堂小结
平方根
概念与表示方法
平方根的性质
开平方
当堂检测
1. 4的平方根是( )A. B. 2 C. -2 D. ±2
D
2. (-0.6)2的平方根是( )A. -0.6 B. 0.6 C. ±0.6 D. 0.36
C
当堂检测
3. 的平方根是±,用数学式子表示为( )A. =± B.= C.±=± D.±=±
C
当堂检测
4.如果-b是a的平方根,那么( )A. b=a2 B. a=b2 C. b=-a2 D. a=-b2
B
5.下列有关平方根的叙述,正确的个数是( )①如果a存在平方根,那么a>0;②如果a有两个不相等的平方根,那么a>0;③如果a没有平方根,那么a<0;④如果a>0,那么a的平方根也大于0.A.1 B.2 C.3 D.4
B
当堂检测
6.若一个数的平方等于2,则这个数等于________.
±
7.若3x+2有平方根,则x的取值范围为_________.
x≥-
8.一个正数的两个不同的平方根分别是a-1和5-2a,则这个正数是_____.
9
10.写出下列各数的平方根:
81,289,0,2 ,2.56,0.81,(-2)4
当堂检测
(1) 4x2=81; (2)5x2-10=0; (3) (x-1)2=36.
11.求下列各式中x的值:
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
