24.2.2直线和圆的位置关系第二课时 课件(共23张PPT)-2023-2024学年九年级数学上册同步精品课件(人教版)
文档属性
| 名称 | 24.2.2直线和圆的位置关系第二课时 课件(共23张PPT)-2023-2024学年九年级数学上册同步精品课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 20:01:48 | ||
图片预览






文档简介
第二十四章
圆
24.2 直线和圆的位置关系
第2课时 切线的判定与性质
教学目标/Teaching aims
1
会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.
3
能运用圆的切线的判定定理和性质定理解决问题.
2
理解并掌握圆的切线的判定定理及性质定理.
复习回顾
回顾:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
什么是圆的切线?
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
情景导入
生活中的切线
新知探究
思考:
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,
则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
l
O
A
圆心O到直线l的距离就⊙o的半径
直线l就是⊙O的切线
新知探究
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
l
O
A
∵OA为⊙O的半径
BC ⊥ OA于A
∴BC为⊙O的切线
应用格式:
新知探究
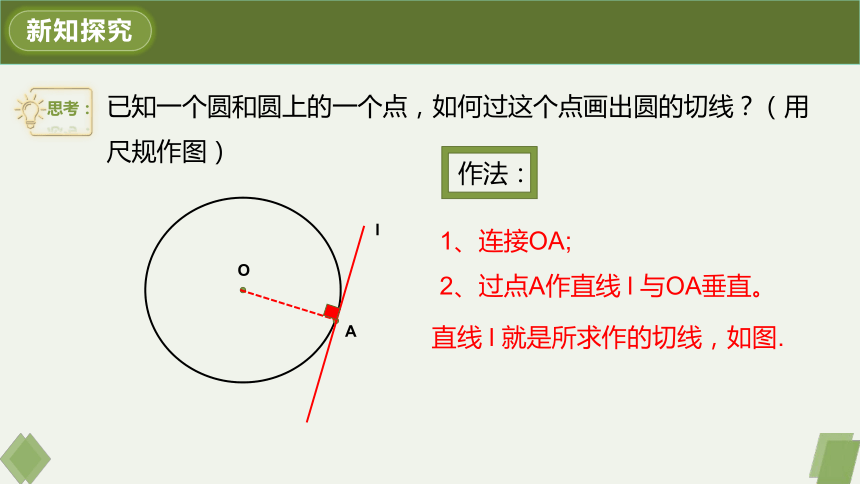
已知一个圆和圆上的一个点,如何过这个点画出圆的切线?(用尺规作图)
思考:
作法:
1、连接OA;
O
A
2、过点A作直线 l 与OA垂直。
l
直线 l 就是所求作的切线,如图.
归纳小结
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
l
O
A
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
巩固练习
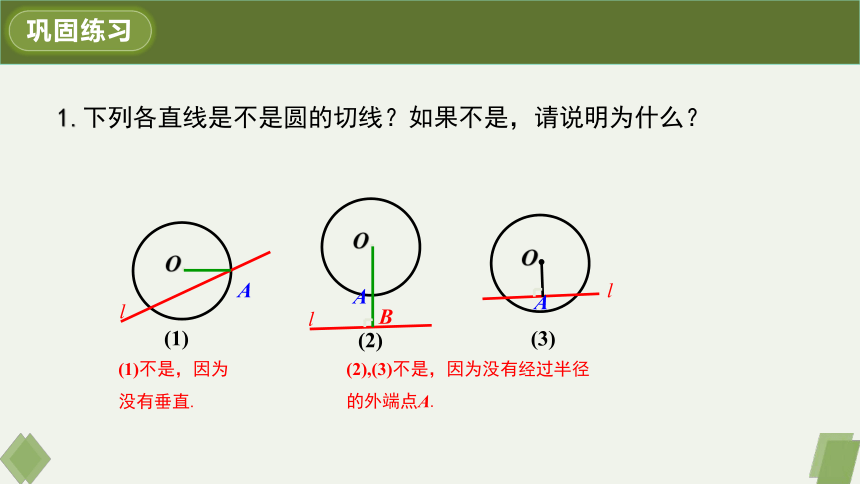
1.下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
新知探究
A
l
O
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
切线性质
圆的切线垂直于经过切点的半径.
应用格式
思考:在⊙O中,如果直线 l 是⊙O的切线,切点为A,那么半径OA与直线 l 是不是一定垂直?
新知探究
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OMC
D
B
O
A
(3)所以AB与CD垂直.
M
证法1:反证法.
性质定理的证明
新知探究
C
D
O
A
证法2:构造法.
作出小⊙O的同心圆大⊙O,CD切小⊙O于点A,且A点为CD的中点,连接OA,根据垂径定理,则CD ⊥OA,即圆的切线垂直于经过切点的半径.
巩固练习
1. 如图,△ABC 为等腰三角形,O 是底边BC的中点,腰AB与⊙O相切于D.求证:AC 是⊙O 的切线.
证明:连接OD,OA, 过O 作OE ⊥AC.
∵⊙O 与AB 相切于D ,
∴OD ⊥ AB.
又∵△ABC 中,AB=AC ,O是BC 的中点.
∴AO 平分∠BAC,
又OD⊥AB ,OE⊥AC.
∴OD=OE.
∵OD 是⊙O 半径,OD=OE,OE⊥ AC.
∴AC 是⊙O 的切线.
巩固练习
2. 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
证明:连接OC(如图).
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
巩固练习
3. 如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,
OP=OA+PA=2+r.
在Rt△OBP中,OB2+PB2=PO2,即r2+42=(2+r)2.
解得 r=3,即⊙O的半径为3.
归纳小结
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
课堂练习
1.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线. ( )
(2)垂直于半径的直线是圆的切线. ( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
(4) 和圆只有一个公共点的直线是圆的切线. ( )
(5)过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
课堂练习
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 ,
相切
课堂练习
3.如图,在☉O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )
A.40° B.35° C.30° D.45°
C
课堂练习
4.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E. 求证:PE是⊙O的切线.
证明:连接OP.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C. ∴OP∥AC.
∵PE⊥AC, ∴PE⊥OP.
∴PE为⊙O的切线.
课堂练习
5.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,∴OM⊥BC.
又∵ON⊥CD,O为正方形ABCD对角线AC上一点,
∴OM=ON,
∴CD与⊙O相切.
课堂总结
24.2 直线和圆的位置关系
第2课时 切线的判定与性质
谢谢观看
圆
圆
24.2 直线和圆的位置关系
第2课时 切线的判定与性质
教学目标/Teaching aims
1
会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.
3
能运用圆的切线的判定定理和性质定理解决问题.
2
理解并掌握圆的切线的判定定理及性质定理.
复习回顾
回顾:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
什么是圆的切线?
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
情景导入
生活中的切线
新知探究
思考:
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,
则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
l
O
A
圆心O到直线l的距离就⊙o的半径
直线l就是⊙O的切线
新知探究
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
l
O
A
∵OA为⊙O的半径
BC ⊥ OA于A
∴BC为⊙O的切线
应用格式:
新知探究
已知一个圆和圆上的一个点,如何过这个点画出圆的切线?(用尺规作图)
思考:
作法:
1、连接OA;
O
A
2、过点A作直线 l 与OA垂直。
l
直线 l 就是所求作的切线,如图.
归纳小结
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
l
O
A
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
巩固练习
1.下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
新知探究
A
l
O
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
切线性质
圆的切线垂直于经过切点的半径.
应用格式
思考:在⊙O中,如果直线 l 是⊙O的切线,切点为A,那么半径OA与直线 l 是不是一定垂直?
新知探究
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OM
D
B
O
A
(3)所以AB与CD垂直.
M
证法1:反证法.
性质定理的证明
新知探究
C
D
O
A
证法2:构造法.
作出小⊙O的同心圆大⊙O,CD切小⊙O于点A,且A点为CD的中点,连接OA,根据垂径定理,则CD ⊥OA,即圆的切线垂直于经过切点的半径.
巩固练习
1. 如图,△ABC 为等腰三角形,O 是底边BC的中点,腰AB与⊙O相切于D.求证:AC 是⊙O 的切线.
证明:连接OD,OA, 过O 作OE ⊥AC.
∵⊙O 与AB 相切于D ,
∴OD ⊥ AB.
又∵△ABC 中,AB=AC ,O是BC 的中点.
∴AO 平分∠BAC,
又OD⊥AB ,OE⊥AC.
∴OD=OE.
∵OD 是⊙O 半径,OD=OE,OE⊥ AC.
∴AC 是⊙O 的切线.
巩固练习
2. 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
证明:连接OC(如图).
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
巩固练习
3. 如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,
OP=OA+PA=2+r.
在Rt△OBP中,OB2+PB2=PO2,即r2+42=(2+r)2.
解得 r=3,即⊙O的半径为3.
归纳小结
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
课堂练习
1.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线. ( )
(2)垂直于半径的直线是圆的切线. ( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
(4) 和圆只有一个公共点的直线是圆的切线. ( )
(5)过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
课堂练习
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 ,
相切
课堂练习
3.如图,在☉O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )
A.40° B.35° C.30° D.45°
C
课堂练习
4.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E. 求证:PE是⊙O的切线.
证明:连接OP.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C. ∴OP∥AC.
∵PE⊥AC, ∴PE⊥OP.
∴PE为⊙O的切线.
课堂练习
5.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,∴OM⊥BC.
又∵ON⊥CD,O为正方形ABCD对角线AC上一点,
∴OM=ON,
∴CD与⊙O相切.
课堂总结
24.2 直线和圆的位置关系
第2课时 切线的判定与性质
谢谢观看
圆
同课章节目录
