24.4 第1课时 弧长和扇形面积 课件(共27张PPT)-2023-2024学年九年级数学上册同步精品课件(人教版)
文档属性
| 名称 | 24.4 第1课时 弧长和扇形面积 课件(共27张PPT)-2023-2024学年九年级数学上册同步精品课件(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 20:00:49 | ||
图片预览








文档简介
第24章
圆
24.4弧长和扇形面积(第1课时)
教学目标/Teaching aims
1
经历弧长公式和扇形面积公式的推导过程,能运用弧长公式和扇形面积进行有关计算;
3
通过弧长公式和扇形面积公式的推导,感受数学的严谨性以及数学结论通过使用公式解决实际问题,让学生体验数学与人类生活的密切联系,激发学生学习数学的兴趣.
2
通过弧长和扇形面积公式的推导过程与运用,培养学生的探索和归纳能力,发展学生分析问题、解决问题的能力;
情景导入
在田径200米跑比赛中,运动员的起跑位置相同吗?为什么?
起跑位置不同,为了保证每个人所跑路程为200米
每个跑道应该相距多远呢,关键是应该知道这些弯道的“展直长度”,,如何计算呢?
新知探究
思考:
我们知道,弧是圆的一部分,弧长就是圆周长的一部分.想一想,如何计算圆周长?
圆的周长可以看作是多少度的圆心角所对的弧长?
1°的圆心角所对的弧长是多少?
新知探究
n°的圆心角所对的弧长是多少?
O
A
R
B
弧长公式
用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
巩固练习
(1)在半径为6cm的圆中,求30°的圆心角所对的弧长:
(2)一条弧的长为3 πcm,弧的半径为6cm,求这条弧所对的圆心角:
得
新知探究
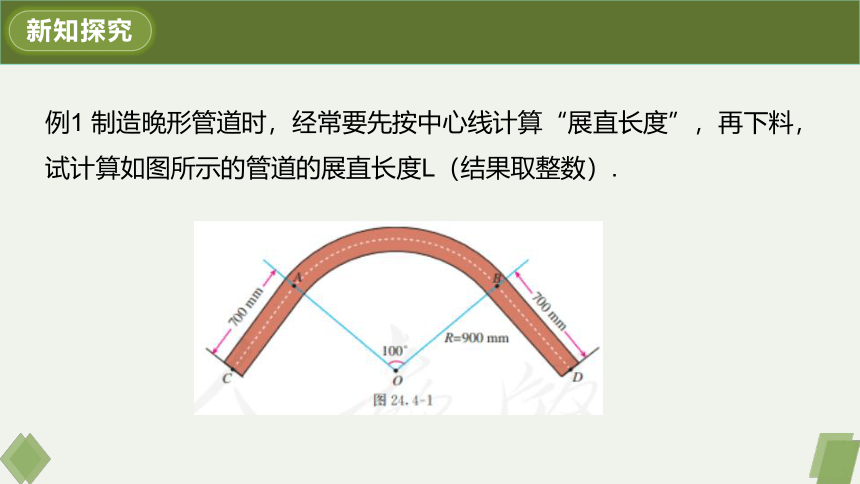
例1 制造晚形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图所示的管道的展直长度L(结果取整数).
新知探究
解:由弧长公式,可得弧AB的长
因此所要求的展直长度l=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
归纳小结
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子
表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,
都可求出第三个量.
弧长公式
新知探究
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
如图,绿色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
巩固练习
辨析:下列图片中哪些是扇形,为什么?
(1) (2) (3) (4) (5)
(1)(2)(4)不是;(3)(5)是
新知探究
思考:
由扇形的定义可知,扇形面积就是圆面积的一部分.想一想,如何计算圆的面积?
圆面积可以看作是多少度的圆心角所对的扇形的面积?
1°的圆心角所对的扇形面积是多少?
新知探究
n°的圆心角所对的扇形面积是多少?
O
A
R
n
B
O
A
R
n
B
扇形
归纳小结
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
巩固练习
(1)若扇形的半径为6cm,圆心角为60°,求扇形的面积
(2)已知扇形所在圆的半径为3cm,弧长为20πcm,求扇形面积
新知探究
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)
讨论:(1)截面上有水部分的面积是指图上哪一部分?
阴影部分.
(1)
O .
B
A
C
O.
B
A
C
D
(2)
O.
B
A
C
D
(3)
(2)水面高0.3 m是指哪一条线段的长?这条线段应该怎样画出来?
线段DC.过点O作OD垂直符号于AB并长交圆O于C.
(3)要求图中阴影部分面积,应该怎么办?
阴影部分面积=扇形OAB的面积- △OAB的面积
新知探究
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60?, ∠AOB=120?.
O.
B
A
C
D
(3)
新知探究
有水部分的面积:
S=S扇形OAB - SΔOAB
O
B
A
C
D
(3)
新知探究
归纳小结
O
O
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
弓形的面积公式
课堂练习
1.已知扇形的圆心角为50°,半径是18,则该扇形的弧长为 ( )
A.2π B.3π
C.4π D.5π
D
课堂练习
B
课堂练习
3.一个扇形的弧长是11π cm,半径是18 cm,则该扇形的圆心角是_________.
4.若一个扇形的面积为6π,圆心角为45°,则该扇形的半径为_______.
110°
课堂练习
15π
课堂练习
6.如图,点P的坐标为(1 , 3),把点P绕坐标原点O逆时针旋转90°后得到点Q.则点P运动的路径长为______,点Q的坐标是_________.
(-3 , 1)
课堂总结
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
24.4弧长和扇形面积(第1课时)
谢谢观看
圆
圆
24.4弧长和扇形面积(第1课时)
教学目标/Teaching aims
1
经历弧长公式和扇形面积公式的推导过程,能运用弧长公式和扇形面积进行有关计算;
3
通过弧长公式和扇形面积公式的推导,感受数学的严谨性以及数学结论通过使用公式解决实际问题,让学生体验数学与人类生活的密切联系,激发学生学习数学的兴趣.
2
通过弧长和扇形面积公式的推导过程与运用,培养学生的探索和归纳能力,发展学生分析问题、解决问题的能力;
情景导入
在田径200米跑比赛中,运动员的起跑位置相同吗?为什么?
起跑位置不同,为了保证每个人所跑路程为200米
每个跑道应该相距多远呢,关键是应该知道这些弯道的“展直长度”,,如何计算呢?
新知探究
思考:
我们知道,弧是圆的一部分,弧长就是圆周长的一部分.想一想,如何计算圆周长?
圆的周长可以看作是多少度的圆心角所对的弧长?
1°的圆心角所对的弧长是多少?
新知探究
n°的圆心角所对的弧长是多少?
O
A
R
B
弧长公式
用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
巩固练习
(1)在半径为6cm的圆中,求30°的圆心角所对的弧长:
(2)一条弧的长为3 πcm,弧的半径为6cm,求这条弧所对的圆心角:
得
新知探究
例1 制造晚形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图所示的管道的展直长度L(结果取整数).
新知探究
解:由弧长公式,可得弧AB的长
因此所要求的展直长度l=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
归纳小结
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子
表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,
都可求出第三个量.
弧长公式
新知探究
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
如图,绿色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
巩固练习
辨析:下列图片中哪些是扇形,为什么?
(1) (2) (3) (4) (5)
(1)(2)(4)不是;(3)(5)是
新知探究
思考:
由扇形的定义可知,扇形面积就是圆面积的一部分.想一想,如何计算圆的面积?
圆面积可以看作是多少度的圆心角所对的扇形的面积?
1°的圆心角所对的扇形面积是多少?
新知探究
n°的圆心角所对的扇形面积是多少?
O
A
R
n
B
O
A
R
n
B
扇形
归纳小结
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
巩固练习
(1)若扇形的半径为6cm,圆心角为60°,求扇形的面积
(2)已知扇形所在圆的半径为3cm,弧长为20πcm,求扇形面积
新知探究
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)
讨论:(1)截面上有水部分的面积是指图上哪一部分?
阴影部分.
(1)
O .
B
A
C
O.
B
A
C
D
(2)
O.
B
A
C
D
(3)
(2)水面高0.3 m是指哪一条线段的长?这条线段应该怎样画出来?
线段DC.过点O作OD垂直符号于AB并长交圆O于C.
(3)要求图中阴影部分面积,应该怎么办?
阴影部分面积=扇形OAB的面积- △OAB的面积
新知探究
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60?, ∠AOB=120?.
O.
B
A
C
D
(3)
新知探究
有水部分的面积:
S=S扇形OAB - SΔOAB
O
B
A
C
D
(3)
新知探究
归纳小结
O
O
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
弓形的面积公式
课堂练习
1.已知扇形的圆心角为50°,半径是18,则该扇形的弧长为 ( )
A.2π B.3π
C.4π D.5π
D
课堂练习
B
课堂练习
3.一个扇形的弧长是11π cm,半径是18 cm,则该扇形的圆心角是_________.
4.若一个扇形的面积为6π,圆心角为45°,则该扇形的半径为_______.
110°
课堂练习
15π
课堂练习
6.如图,点P的坐标为(1 , 3),把点P绕坐标原点O逆时针旋转90°后得到点Q.则点P运动的路径长为______,点Q的坐标是_________.
(-3 , 1)
课堂总结
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
24.4弧长和扇形面积(第1课时)
谢谢观看
圆
同课章节目录
