13.3.2.2 含30°角的直角三角形的性质 课件(共24张PPT)-2023-2024学年八年级数学上册同步精品课堂(人教版)
文档属性
| 名称 | 13.3.2.2 含30°角的直角三角形的性质 课件(共24张PPT)-2023-2024学年八年级数学上册同步精品课堂(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 31.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 19:59:49 | ||
图片预览



文档简介
(共24张PPT)
第13章
轴对称
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
13.3.2.2
含30°角的直角
三角形的性质
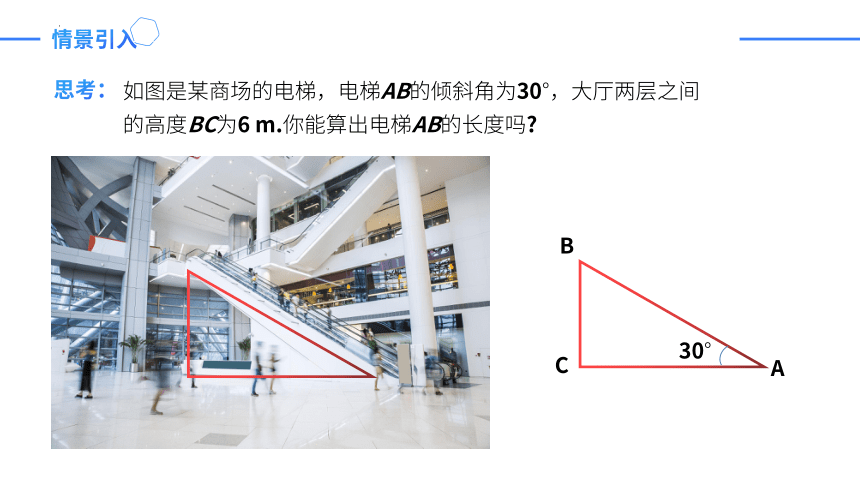
情景引入
如图是某商场的电梯,电梯AB的倾斜角为30°,大厅两层之间
的高度BC为6 m.你能算出电梯AB的长度吗
思考:
B
A
C
30°
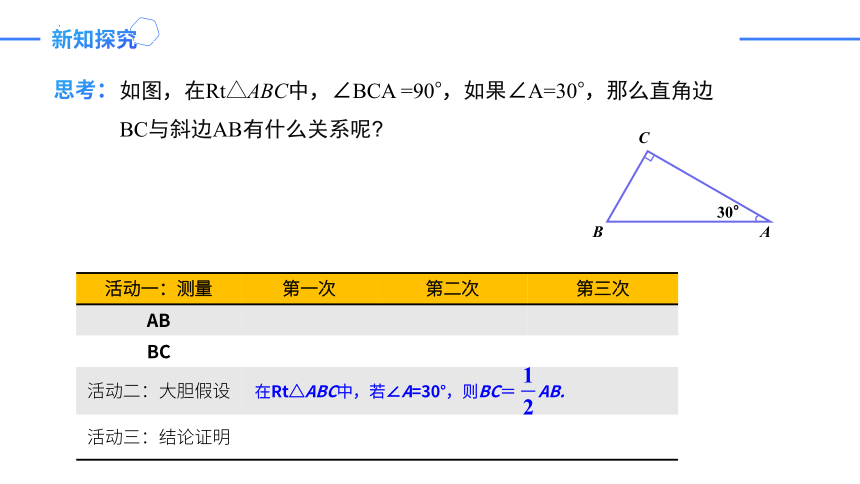
新知探究
思考:
如图,在Rt△ABC中,∠BCA =90°,如果∠A=30°,那么直角边 BC与斜边AB有什么关系呢
C
B
A
30°
活动一:测量 第一次 第二次 第三次
AB
BC
活动二:大胆假设 活动三:结论证明
在Rt△ABC中,若∠A=30°,则BC= AB.
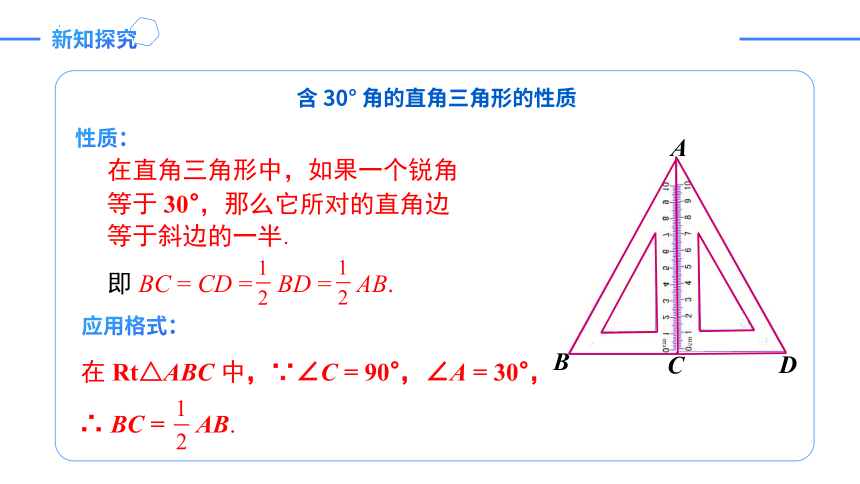
新知探究
含 30° 角的直角三角形的性质
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
即 BC = CD = BD = AB.
性质:
应用格式:
在 Rt△ABC 中,∵∠C = 90°,∠A = 30°,
∴ BC = AB.
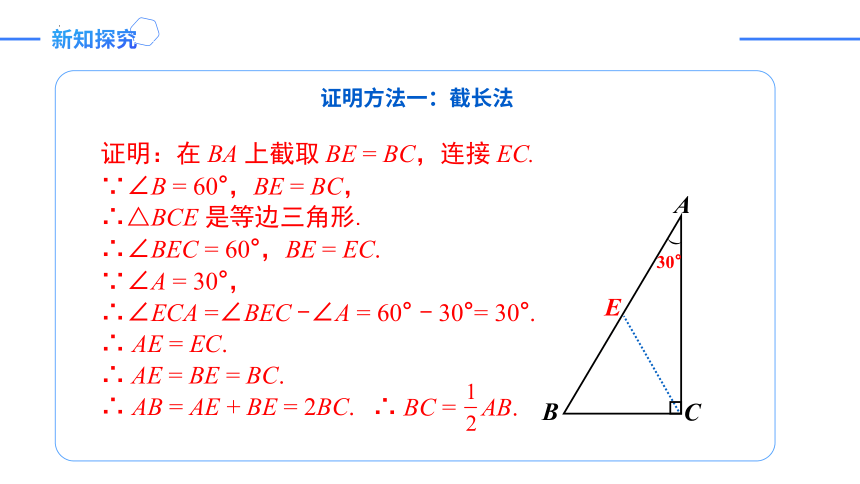
新知探究
证明方法一:截长法
)
证明:在 BA 上截取 BE = BC,连接 EC.
∵∠B = 60°,BE = BC,
∴△BCE 是等边三角形.
∴∠BEC = 60°,BE = EC.
∵∠A = 30°,
∴∠ECA =∠BEC -∠A = 60° - 30°= 30°.
∴ AE = EC.
∴ AE = BE = BC.
∴ AB = AE + BE = 2BC.
E
A
B
C
∴ BC = AB.
30°
新知探究
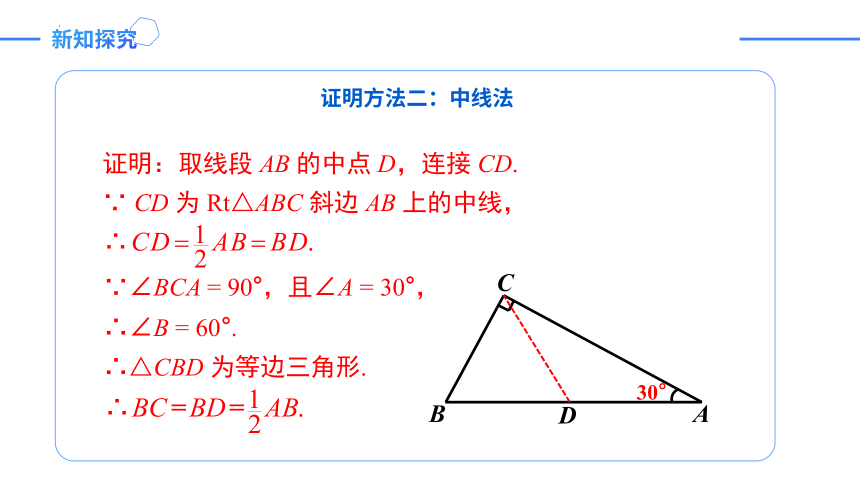
证明方法二:中线法
证明:取线段 AB 的中点 D,连接 CD.
∵ CD 为 Rt△ABC 斜边 AB 上的中线,
A
30°
B
C
D
∵∠BCA = 90°,且∠A = 30°,
∴∠B = 60°.
∴△CBD 为等边三角形.
新知探究
证明方法三:倍长法
证明:在△ABC 中,
∵∠ACB = 90°,∠BAC = 30°,
∴∠B = 60°.
延长 BC 到 D,使 BD = AB,连接 AD,
则△ABD 是等边三角形.
A
B
C
D
∴ BC = BD = AB.
30°
)
新知探究
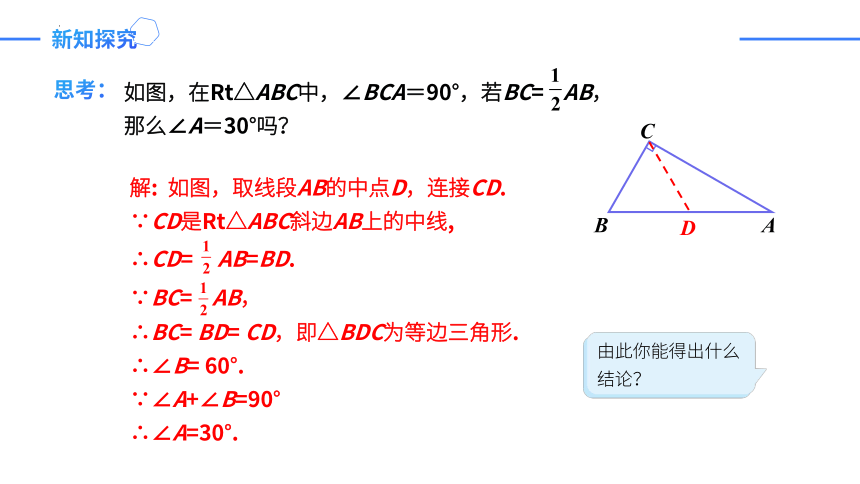
思考:
如图,在Rt△ABC中,∠BCA=90°,若BC= AB,
那么∠A=30°吗?
C
B
A
D
解: 如图,取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD= AB=BD.
∵BC= AB,
∴BC= BD= CD,即△BDC为等边三角形.
∴∠B= 60°.
∵∠A+∠B=90°
∴∠A=30°.
由此你能得出什么结论?
新知探究
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
互为逆命题
典例精析
例1
如图是某商场的电梯,电梯AB的倾斜角为30°,大厅两层之间
的高度BC为6 m.你能算出电梯AB的长度吗
B
A
C
30°
解:在 Rt△ABC 中,∵∠C = 90°,∠A = 30°,
∴ AB=2BC=12m.
典例精析
例2
如图,在△ABC中,已知∠ACB=90°,CD垂直于AB,垂足为点D,∠A=30°.求证: AB=4BD.
解:在Rt△ABC中,∵∠A=30°, ∴BC= AB.
又∠A+∠B=90°,
∴∠B=60°.
在Rt△BCD中,∵∠B+∠BCD=90°,
∴∠BCD=90°-∠B=30°.
故BD= BC.
又BC= AB,
则BD= AB,即AB=4BD.
典例精析
例3
如图,线段AE与BC相交于点D,BD=CD, AD=ED, CA⊥AE,∠1=30°,
且AB=3 cm.那么线段BE多长呢
解:
典例精析
例4
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=2,CD是斜边上的中线,CE是高,F是CD的中点.
(1)求CD的长;
(2)证明:△EDF为等边三角形.
典例精析
例5
将一副三角尺如图所示叠放在一起,若AB=14 cm,求阴影部分
△ACF的面积.
解:
典例精析
例6
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°. 小芳朝正前方笔直行走400 m,此时测得塔尖的仰角为30°.若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗
解:
典例精析
例7
在△ABC 中,AB = AC,∠BAC = 120°,D 是 BC 的中点,DE⊥AB 于 E 点,求证:BE = 3AE.
证明:∵ AB = AC,∠BAC = 120°,
∴∠B =∠C = 30°.
∵ D 是 BC 的中点,∴ AD⊥BC.
∴∠ADC = 90°,∠BAD =∠DAC = 60°.
∴ AB = 2AD. ∵ DE⊥AB,∴∠AED = 90°.
∴∠ADE = 30°,∴ AD = 2AE.
∴ AB = 4AE. ∴ BE = 3AE.
归纳总结
要点
注意
前提条件:含 30° 角的直角三角形中
在直角三角形中,如果一个锐角等于 30°,
那么它所对的直角边等于斜边的一半
含 30°角的直角
三角形的性质
找准 30° 的角所对的直角边,点明斜边
内容
当堂检测
1.已知△ABC中,∠A:∠B:∠C=1: 2: 3,最短边BC=4 cm, 则最长边AB的长是( )
A、5cm B、6 cm
C、7cm D、8 cm
D
解析: ∠A:∠B:∠C=1: 2: 3, ∠A+∠B+∠C=180°
∴ ∠A=30°, ∠B=60°, ∠C=90°
∵BC=4 cm ∴ AB=2BC=8cm
当堂检测
2. 如图,在 △ABC 中,∠ACB = 90°,CD 是高,∠A = 30°,AB = 4.则 BD 的长为 .
A
B
C
D
1
3. 在△ABC中,∠A∶∠B∶∠C = 1∶2∶3,若 AB = 10,
则 BC 的长为 .
5
4. 如图,Rt△ABC 中,∠A = 30°,AB + BC = 12 cm,则
AB =______cm.
A
C
B
8
第4题图
当堂检测
5.如图,是屋架设计图的一部分,点D是斜梁AB的中点,BC为立柱,DE垂直于横梁AC,AB=7.4m, ∠A=30 ° ,求立柱BC,DE的长.
A
B
C
D
E
解:在△ABC中,
∵ BC⊥AC ,∠A=30°,
∴BC= AB= ×7.4=3.7(m).
∵ 点D是AB的中点 ,
∴ AD= AB=3.7(m).
在△ADE中,∵ DE⊥AC ,∠A=30°,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m,DE的长是1.85m.
当堂检测
6.一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘轮船上午8:00从A处出发,10:00到达B处,从B处测得一礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;(2)求出B处到礁石C的距离.
B
C
30°
60°
A
D
解:(1)如图,以B为顶点,向北偏西60°作角,
这角一边与AM交于点C, 则C为礁石所在地.
M
北
(2)∵∠DBC=∠BAC+∠ACB,∠BAC=30 °, ∠DBC=60°,
∴∠ACB=30°,即∠BAC=∠ACB,
∴BC=AB ( 等角对等边) , 即 BC=AB=10×2=20(海里).
答:B处到礁石C的距离为20海里.
当堂检测
7.如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 cm,∠A = 30°,立柱 BC、DE 有多长?
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A = 30°,
∴ BC = AB,DE = AD.
∴ BC = AB = ×7.4 = 3.7.
又 AD = AB = 3.7,
∴ DE = AD = ×3.7 = 1.85.
答:立柱 BC 的长是 3.7 m,DE 的长是 1.85 m.
当堂检测
8. 如图,已知△ABC 是等边三角形,D,E 分别为 BC、AC 上的点,且 CD = AE,AD、BE 相交于点 P,BQ⊥AD 于点 Q, 求证:BP = 2PQ.
∴△ADC≌△BEA (SAS).
证明:∵△ABC 为等边三角形,
∴ AC = BC = AB,∠C =∠BAC = 60°.
∵ CD = AE,
∴∠CAD =∠ABE.
∵∠BAP +∠CAD = 60°,
∴∠BAP +∠ABE = 60°,即∠BPQ = 60°.
又∵ BQ⊥AD,
∴ BP = 2PQ.
∴∠PBQ = 30°.
∴∠BQP = 90°.
第13章
轴对称
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
13.3.2.2
含30°角的直角
三角形的性质
情景引入
如图是某商场的电梯,电梯AB的倾斜角为30°,大厅两层之间
的高度BC为6 m.你能算出电梯AB的长度吗
思考:
B
A
C
30°
新知探究
思考:
如图,在Rt△ABC中,∠BCA =90°,如果∠A=30°,那么直角边 BC与斜边AB有什么关系呢
C
B
A
30°
活动一:测量 第一次 第二次 第三次
AB
BC
活动二:大胆假设 活动三:结论证明
在Rt△ABC中,若∠A=30°,则BC= AB.
新知探究
含 30° 角的直角三角形的性质
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
即 BC = CD = BD = AB.
性质:
应用格式:
在 Rt△ABC 中,∵∠C = 90°,∠A = 30°,
∴ BC = AB.
新知探究
证明方法一:截长法
)
证明:在 BA 上截取 BE = BC,连接 EC.
∵∠B = 60°,BE = BC,
∴△BCE 是等边三角形.
∴∠BEC = 60°,BE = EC.
∵∠A = 30°,
∴∠ECA =∠BEC -∠A = 60° - 30°= 30°.
∴ AE = EC.
∴ AE = BE = BC.
∴ AB = AE + BE = 2BC.
E
A
B
C
∴ BC = AB.
30°
新知探究
证明方法二:中线法
证明:取线段 AB 的中点 D,连接 CD.
∵ CD 为 Rt△ABC 斜边 AB 上的中线,
A
30°
B
C
D
∵∠BCA = 90°,且∠A = 30°,
∴∠B = 60°.
∴△CBD 为等边三角形.
新知探究
证明方法三:倍长法
证明:在△ABC 中,
∵∠ACB = 90°,∠BAC = 30°,
∴∠B = 60°.
延长 BC 到 D,使 BD = AB,连接 AD,
则△ABD 是等边三角形.
A
B
C
D
∴ BC = BD = AB.
30°
)
新知探究
思考:
如图,在Rt△ABC中,∠BCA=90°,若BC= AB,
那么∠A=30°吗?
C
B
A
D
解: 如图,取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD= AB=BD.
∵BC= AB,
∴BC= BD= CD,即△BDC为等边三角形.
∴∠B= 60°.
∵∠A+∠B=90°
∴∠A=30°.
由此你能得出什么结论?
新知探究
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
互为逆命题
典例精析
例1
如图是某商场的电梯,电梯AB的倾斜角为30°,大厅两层之间
的高度BC为6 m.你能算出电梯AB的长度吗
B
A
C
30°
解:在 Rt△ABC 中,∵∠C = 90°,∠A = 30°,
∴ AB=2BC=12m.
典例精析
例2
如图,在△ABC中,已知∠ACB=90°,CD垂直于AB,垂足为点D,∠A=30°.求证: AB=4BD.
解:在Rt△ABC中,∵∠A=30°, ∴BC= AB.
又∠A+∠B=90°,
∴∠B=60°.
在Rt△BCD中,∵∠B+∠BCD=90°,
∴∠BCD=90°-∠B=30°.
故BD= BC.
又BC= AB,
则BD= AB,即AB=4BD.
典例精析
例3
如图,线段AE与BC相交于点D,BD=CD, AD=ED, CA⊥AE,∠1=30°,
且AB=3 cm.那么线段BE多长呢
解:
典例精析
例4
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=2,CD是斜边上的中线,CE是高,F是CD的中点.
(1)求CD的长;
(2)证明:△EDF为等边三角形.
典例精析
例5
将一副三角尺如图所示叠放在一起,若AB=14 cm,求阴影部分
△ACF的面积.
解:
典例精析
例6
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°. 小芳朝正前方笔直行走400 m,此时测得塔尖的仰角为30°.若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗
解:
典例精析
例7
在△ABC 中,AB = AC,∠BAC = 120°,D 是 BC 的中点,DE⊥AB 于 E 点,求证:BE = 3AE.
证明:∵ AB = AC,∠BAC = 120°,
∴∠B =∠C = 30°.
∵ D 是 BC 的中点,∴ AD⊥BC.
∴∠ADC = 90°,∠BAD =∠DAC = 60°.
∴ AB = 2AD. ∵ DE⊥AB,∴∠AED = 90°.
∴∠ADE = 30°,∴ AD = 2AE.
∴ AB = 4AE. ∴ BE = 3AE.
归纳总结
要点
注意
前提条件:含 30° 角的直角三角形中
在直角三角形中,如果一个锐角等于 30°,
那么它所对的直角边等于斜边的一半
含 30°角的直角
三角形的性质
找准 30° 的角所对的直角边,点明斜边
内容
当堂检测
1.已知△ABC中,∠A:∠B:∠C=1: 2: 3,最短边BC=4 cm, 则最长边AB的长是( )
A、5cm B、6 cm
C、7cm D、8 cm
D
解析: ∠A:∠B:∠C=1: 2: 3, ∠A+∠B+∠C=180°
∴ ∠A=30°, ∠B=60°, ∠C=90°
∵BC=4 cm ∴ AB=2BC=8cm
当堂检测
2. 如图,在 △ABC 中,∠ACB = 90°,CD 是高,∠A = 30°,AB = 4.则 BD 的长为 .
A
B
C
D
1
3. 在△ABC中,∠A∶∠B∶∠C = 1∶2∶3,若 AB = 10,
则 BC 的长为 .
5
4. 如图,Rt△ABC 中,∠A = 30°,AB + BC = 12 cm,则
AB =______cm.
A
C
B
8
第4题图
当堂检测
5.如图,是屋架设计图的一部分,点D是斜梁AB的中点,BC为立柱,DE垂直于横梁AC,AB=7.4m, ∠A=30 ° ,求立柱BC,DE的长.
A
B
C
D
E
解:在△ABC中,
∵ BC⊥AC ,∠A=30°,
∴BC= AB= ×7.4=3.7(m).
∵ 点D是AB的中点 ,
∴ AD= AB=3.7(m).
在△ADE中,∵ DE⊥AC ,∠A=30°,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m,DE的长是1.85m.
当堂检测
6.一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘轮船上午8:00从A处出发,10:00到达B处,从B处测得一礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;(2)求出B处到礁石C的距离.
B
C
30°
60°
A
D
解:(1)如图,以B为顶点,向北偏西60°作角,
这角一边与AM交于点C, 则C为礁石所在地.
M
北
(2)∵∠DBC=∠BAC+∠ACB,∠BAC=30 °, ∠DBC=60°,
∴∠ACB=30°,即∠BAC=∠ACB,
∴BC=AB ( 等角对等边) , 即 BC=AB=10×2=20(海里).
答:B处到礁石C的距离为20海里.
当堂检测
7.如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 cm,∠A = 30°,立柱 BC、DE 有多长?
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A = 30°,
∴ BC = AB,DE = AD.
∴ BC = AB = ×7.4 = 3.7.
又 AD = AB = 3.7,
∴ DE = AD = ×3.7 = 1.85.
答:立柱 BC 的长是 3.7 m,DE 的长是 1.85 m.
当堂检测
8. 如图,已知△ABC 是等边三角形,D,E 分别为 BC、AC 上的点,且 CD = AE,AD、BE 相交于点 P,BQ⊥AD 于点 Q, 求证:BP = 2PQ.
∴△ADC≌△BEA (SAS).
证明:∵△ABC 为等边三角形,
∴ AC = BC = AB,∠C =∠BAC = 60°.
∵ CD = AE,
∴∠CAD =∠ABE.
∵∠BAP +∠CAD = 60°,
∴∠BAP +∠ABE = 60°,即∠BPQ = 60°.
又∵ BQ⊥AD,
∴ BP = 2PQ.
∴∠PBQ = 30°.
∴∠BQP = 90°.
