人教版六年级数学下册《圆柱的表面积》课件(共24张PPT)
文档属性
| 名称 | 人教版六年级数学下册《圆柱的表面积》课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
圆柱的表面积
人教版数学六年级下册
情境设疑,导出课题
1
探究总结
3
展开探究,推导公式
2
解决例题,巩固所学
4
爱心捐赠
某文具厂老板将要为贫困地区的孩子
捐献圆柱形的笔筒
制作一个圆柱形的带盖笔筒需要多少硬纸板
要想解决这个问题,
我们需要做的是什么?
想知道制作一个笔筒需要多少硬纸板,
实际上就是计算笔筒的表面积
也就是计算圆柱体的表面积
圆柱包含3个面,分别为上下底面和侧面,
它的表面积就是上下底面和侧面的面积和。
接下来老师将为大家每人分发一个笔筒的圆柱体模型。
按照手上的学习任务单,
在小组之间进行操作探讨,
看看圆柱的表面积具体如何计算吧。
学习任务单
1.从圆柱到新的图形是怎样转化的?
2.新的图形和圆柱各部分之间有怎样的联系?
3.根据新的图形推导出圆柱表面积的计算公式
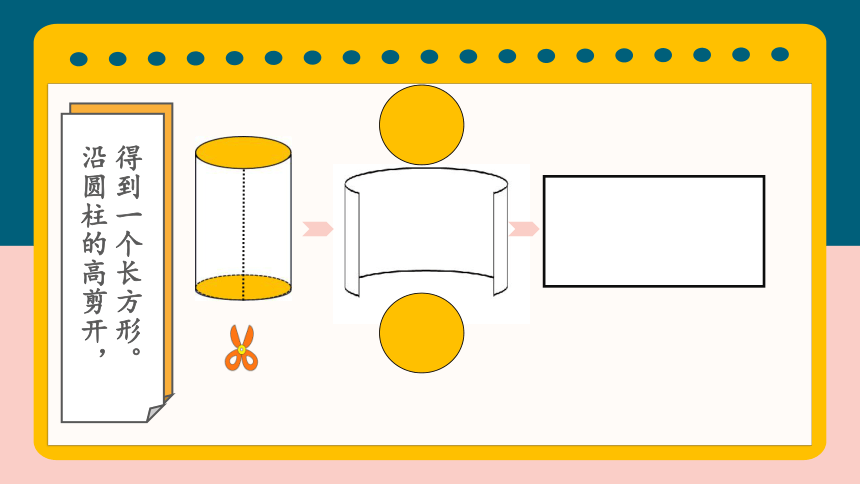
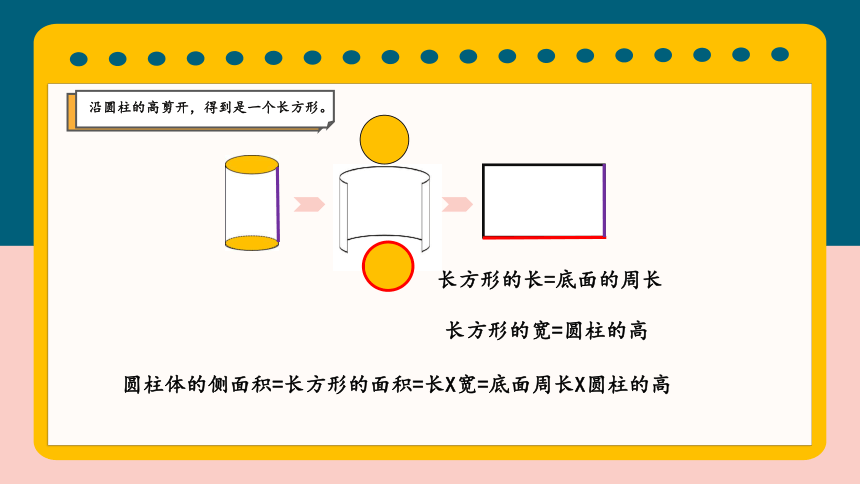
沿圆柱的高剪开,得到一个长方形。
沿圆柱的高剪开,得到是一个长方形。
长方形的长=底面的周长
长方形的宽=圆柱的高
圆柱体的侧面积=长方形的面积=长X宽=底面周长X圆柱的高
沿圆柱的高剪开,得到是一个长方形。
假设底面圆的半径为r,圆柱体的高为h
r
h
底面圆的面积=лr2
圆柱的侧面积=2лrh
圆柱的表面积为:2лr2+2лrh
沿圆柱的高剪开,得到一个正方形。
沿圆柱的高剪开,得到是一个正方形。
正方形的边长=底面的周长
正方形的边长=圆柱的高
圆柱的侧面积=正方形的面积=边长X边长=底面周长X圆柱的高
圆柱的侧面展开图是正方形时,圆柱的底面周长=圆柱的高
沿圆柱的高剪开,得到是一个正方形。
假设底面圆的半径为r,圆柱体的高为h
底面圆的面积=лr2
圆柱的侧面积=2лrh
圆柱的表面积为:2лr2+2лrh
r
h
一起探究一下如果沿着斜线将圆柱体的侧面展开会是什么情况,此时圆柱体的表面积又该如何求呢?
沿圆柱(侧面)的一条斜线剪开,得到一个平行四边形。
沿圆柱(侧面)的一条斜线剪开,得到一个平行四边形。
平行四边形的底=底面的周长
平行四边形的高=圆柱的高
∟
圆柱的侧面积=平行四边形的面积=底X高=底面周长X圆柱的高
沿圆柱(侧面)的一条斜线剪开,得到一个平行四边形。
∟
假设底面圆的半径为r,圆柱体的高为h
底面圆的面积=лr2
圆柱的侧面积=2лrh
圆柱的表面积为:2лr2+2лrh
r
h
通过以上三种情况的探究,我们发现要想探求圆柱的侧面积,沿着圆柱的高将其侧面剪开比较简便。
要想求圆柱的侧面积,我们只需要知道圆柱底面圆的周长和圆柱的高,底面圆的周长和圆的半径有关。
计算圆柱的表面积,就是计算圆柱上下两个底面圆的面积和侧面的面积和,即“圆柱体的表面积=圆柱的侧面积+两个底面的面积;圆柱的侧面积=底面的周长X圆柱的高”,只需要知道底面圆的半径和圆柱的高即可计算出圆柱的表面积,
想要知道制作这批笔筒需要多少硬纸板,首先要确定底面圆的半径以及圆柱的高,然后根据我们所探究到的圆柱表面积的计算公式计算出一个笔筒需要多少硬纸板,之后根据资助贫困孩子的数量,确定一共需要多少硬纸板。
1. 一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数)
在解决这个问题之前,我们首先需要清楚题中的已知信息是什么,需要我们解决的问题是什么
1. 一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数)
已知信息是“帽子为圆柱体,高为30cm,帽顶的直径为20cm”,要解决的问题是“做这样一顶帽子大约要用多少平方厘米的面料?”也就是求这个帽子的表面积
1. 一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数)
不要忘记题中还有一个隐含的条件,制作圆柱体形的帽子,不需要制作下底面,那么求这个圆柱体的表面积时,只需要求圆柱体的侧面积和一个底面积即可。
2.一个圆柱的高是31.4dm,它的侧面展开后得到一个正方形。这个圆柱的表面积是多少?
结合课堂上的探究过程,侧面展开是正方形,推导出圆柱的高=圆柱的底面周长
圆柱的表面积
人教版数学六年级下册
情境设疑,导出课题
1
探究总结
3
展开探究,推导公式
2
解决例题,巩固所学
4
爱心捐赠
某文具厂老板将要为贫困地区的孩子
捐献圆柱形的笔筒
制作一个圆柱形的带盖笔筒需要多少硬纸板
要想解决这个问题,
我们需要做的是什么?
想知道制作一个笔筒需要多少硬纸板,
实际上就是计算笔筒的表面积
也就是计算圆柱体的表面积
圆柱包含3个面,分别为上下底面和侧面,
它的表面积就是上下底面和侧面的面积和。
接下来老师将为大家每人分发一个笔筒的圆柱体模型。
按照手上的学习任务单,
在小组之间进行操作探讨,
看看圆柱的表面积具体如何计算吧。
学习任务单
1.从圆柱到新的图形是怎样转化的?
2.新的图形和圆柱各部分之间有怎样的联系?
3.根据新的图形推导出圆柱表面积的计算公式
沿圆柱的高剪开,得到一个长方形。
沿圆柱的高剪开,得到是一个长方形。
长方形的长=底面的周长
长方形的宽=圆柱的高
圆柱体的侧面积=长方形的面积=长X宽=底面周长X圆柱的高
沿圆柱的高剪开,得到是一个长方形。
假设底面圆的半径为r,圆柱体的高为h
r
h
底面圆的面积=лr2
圆柱的侧面积=2лrh
圆柱的表面积为:2лr2+2лrh
沿圆柱的高剪开,得到一个正方形。
沿圆柱的高剪开,得到是一个正方形。
正方形的边长=底面的周长
正方形的边长=圆柱的高
圆柱的侧面积=正方形的面积=边长X边长=底面周长X圆柱的高
圆柱的侧面展开图是正方形时,圆柱的底面周长=圆柱的高
沿圆柱的高剪开,得到是一个正方形。
假设底面圆的半径为r,圆柱体的高为h
底面圆的面积=лr2
圆柱的侧面积=2лrh
圆柱的表面积为:2лr2+2лrh
r
h
一起探究一下如果沿着斜线将圆柱体的侧面展开会是什么情况,此时圆柱体的表面积又该如何求呢?
沿圆柱(侧面)的一条斜线剪开,得到一个平行四边形。
沿圆柱(侧面)的一条斜线剪开,得到一个平行四边形。
平行四边形的底=底面的周长
平行四边形的高=圆柱的高
∟
圆柱的侧面积=平行四边形的面积=底X高=底面周长X圆柱的高
沿圆柱(侧面)的一条斜线剪开,得到一个平行四边形。
∟
假设底面圆的半径为r,圆柱体的高为h
底面圆的面积=лr2
圆柱的侧面积=2лrh
圆柱的表面积为:2лr2+2лrh
r
h
通过以上三种情况的探究,我们发现要想探求圆柱的侧面积,沿着圆柱的高将其侧面剪开比较简便。
要想求圆柱的侧面积,我们只需要知道圆柱底面圆的周长和圆柱的高,底面圆的周长和圆的半径有关。
计算圆柱的表面积,就是计算圆柱上下两个底面圆的面积和侧面的面积和,即“圆柱体的表面积=圆柱的侧面积+两个底面的面积;圆柱的侧面积=底面的周长X圆柱的高”,只需要知道底面圆的半径和圆柱的高即可计算出圆柱的表面积,
想要知道制作这批笔筒需要多少硬纸板,首先要确定底面圆的半径以及圆柱的高,然后根据我们所探究到的圆柱表面积的计算公式计算出一个笔筒需要多少硬纸板,之后根据资助贫困孩子的数量,确定一共需要多少硬纸板。
1. 一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数)
在解决这个问题之前,我们首先需要清楚题中的已知信息是什么,需要我们解决的问题是什么
1. 一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数)
已知信息是“帽子为圆柱体,高为30cm,帽顶的直径为20cm”,要解决的问题是“做这样一顶帽子大约要用多少平方厘米的面料?”也就是求这个帽子的表面积
1. 一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数)
不要忘记题中还有一个隐含的条件,制作圆柱体形的帽子,不需要制作下底面,那么求这个圆柱体的表面积时,只需要求圆柱体的侧面积和一个底面积即可。
2.一个圆柱的高是31.4dm,它的侧面展开后得到一个正方形。这个圆柱的表面积是多少?
结合课堂上的探究过程,侧面展开是正方形,推导出圆柱的高=圆柱的底面周长
