人教A版(2019)选择性必修第二册 4.3.1等比数列的概念(共2课时)课件(共61张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册 4.3.1等比数列的概念(共2课时)课件(共61张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 09:58:02 | ||
图片预览








文档简介
人教A版(2019)高中数学选择性必修二
4.3.1等比数列的概念
第一课时
一
二
三
学习目标
理解等比数列的概念
会应用定义及通项公式解决一些实际问题
学习目标
掌握等比数列的通项公式
特殊数列
等差数列
等比数列
概念
通项公式
前n项和公式
应用
数列
概念
表示
表格、图像、通项公式、递推公式
特殊化
类比
单元结构
1、等差数列:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数就叫做等差数列的公差(常用字母“d”表示).
数学表达式:
2、等差中项:
如果三个数 a,A,b 成等差数列,那么A叫做a与b的等差中项.
3、等差数列的通项公式:
( n ≥ 2,n ∈N *)
(2A= a+b )
复习回顾
新课导入
我们知道,等差数列的特征是“从第2项起,每一项与它的前一项的差都等于同一个常数” 。
类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
先从哪些方面研究呢?
新知探究一:等比数列的相关概念
实例1 两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
???????????,????????,????????,…,????????????; ①
??????????????????,????????????????,????????????????,…,????????????????????; ②
??????????,?????????,????????,…,????????????. ③
?
新知探究一:等比数列的相关概念
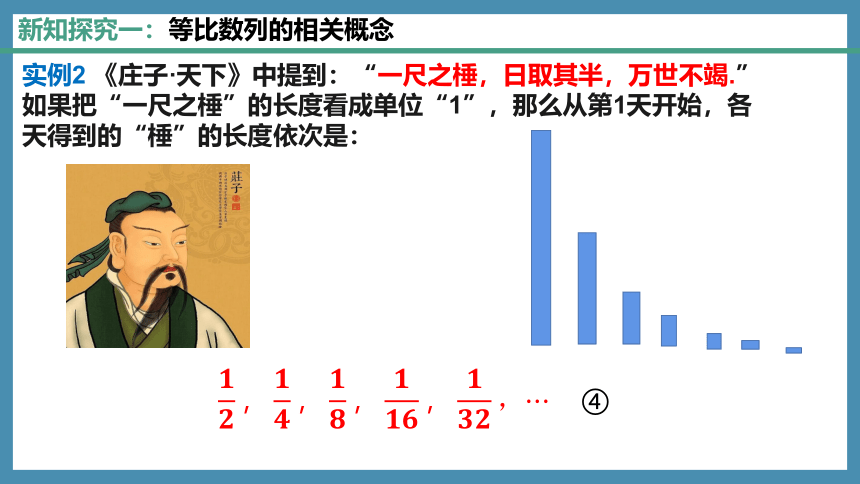
实例2 《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是:
????????,????????,????????,????????????,????????????,??????④
?
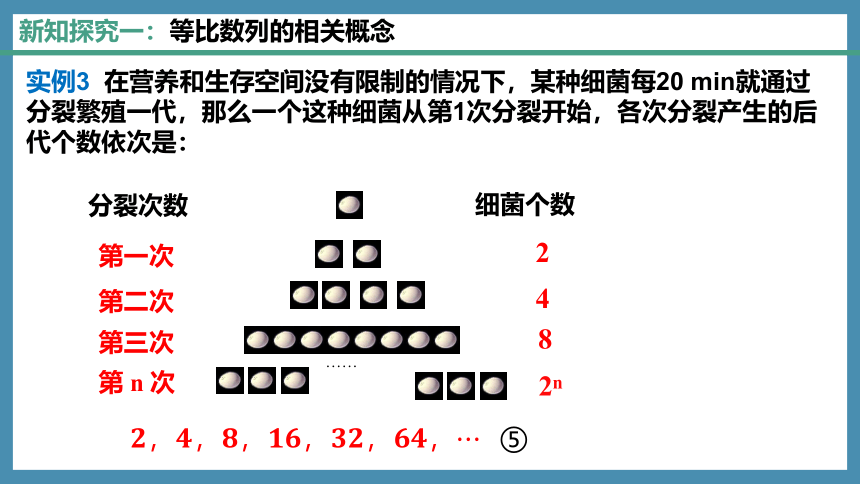
细菌个数
第一次
第二次
第三次
2
4
第 n 次
……
分裂次数
8
2n
实例3 在营养和生存空间没有限制的情况下,某种细菌每20 min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是:
????,????,????,????????,????????,????????,????⑤
?
新知探究一:等比数列的相关概念
新知探究一:等比数列的相关概念
实例4 某人存入银行 ɑ元钱,存期为5年,年利率是r,那么按照复利,他5年内每年末得到的本利和分别是
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息.
????(1+????),????(1+????)2,????(1+????)3,????(1+????)4,????(1+????)5. ⑥
?
问题1 请同学们仔细观察以下六个数列,类比等差数列的研究,你认为可以通过怎样的运算发现以下数列的取值规律?你发现了什么规律?
①
②
③
④
⑤
⑥
取值规律 从第 2 项起,
每一项与它的前一项的比都等于 9.
如果用 表示数列①,那么有
新知探究一:等比数列的相关概念
共同特点: 从第二项起,每一项与前一项的比都等于同一个常数.
????
?
????????????
?
????
?
????????
?
????+????
?
????
?
如果一个数列从第____项起,每一项与它的前一项的___都等于___一个常数,那么这个数列就叫做___________常数叫做等 数列的_____
公比通常用字母 q 表示
二
比
同
等比数列.
公比
如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.常数叫做等差数列的公差.
公差通常用字母d表示
比
an-an-1=d(n≥2,n∈N*)
an+1-an=d(n∈N*)
?????????????????????=????(????≠????,n≥2,n∈N*)
?
????????+????????????=????(????≠????,n∈N*)
?
等差数列的概念
等比数列的概念
问题2 类比等差数列的概念,你能抽象出等比数列的概念吗?
概念生成
符号
(1)
(3) 5,5,5,5,5,5,…
(6)
(2)
思考:观察并判断下列数列是否是等比数列,是的话,指出公比,不是的话请说明理由:
(4) 0,1,2,4,8,…
(5) 2,0,2,0,2,…
是,公比是 2
是,公比是 -2
是,公比是 1
不一定,分类讨论
不是,分母不能为 0
不是,公比不能是 0
概念辨析
1. 判断下列数列是否是等差数列. 如果是,写出它的公差.
课本P31
追问1:等差数列的项、公差均可以是0吗?等比数列呢?
追问2:常数列是等差数列吗?是等比数列吗?
追问3:是否存在既是等差数列又是等比数列的数列?
常数列一定是等差数列,公差为0;
非零常数列是等比数列,公比为1.
非零常数列既是等差数列又是等比数列,公差为0,公比为1.
等差数列的项、公差均可以是0,但等比数列的项和公比均不可以是0
概念辨析
等差中项
等比中项
如果三个数a,A,b组成等差数列,那么A叫做a和b的等差中项.
如果三个数a,G,b组成等比数列,那么G叫做a和b的等比中项
定义
a,A,b成等差数列
a,G,b成等比数列
关系
追问:任意两个实数a,b都有等比中项吗?
若a,b同号则有两个等比中项;若a,b异号则无等比中项.
新知探究二:等比中项
问题3 类比等差中项的概念,你能抽象出等比中项的概念吗?
∴a, G, b成等比数列
?
(ab>0)
新知探究三:等比数列的通项公式
问题4 你能类比等差数列的通项公式推导,根据等比数列的定义及递推公式推导它的通项公式吗?怎么推?
等差数列
类比
法一:不完全归纳法
……
由此归纳等比数列的通项公式可得:
等比数列
新知探究三:等比数列的通项公式
问题4 你能类比等差数列的通项公式推导,根据等比数列的定义及递推公式推导它的通项公式吗?怎么推?
法二:累加法
……
+)
等差数列
类比
……
由等比数列的定义 ?????????????????????=????(????≥????,????∈?????)得
?
n-1个
又a1=a1q0=a1q1-1,即当n=1时上式也成立.
an=a1qn-1 (n∈ ?????)
?
累乘法
等比数列的通项公式:
问题5 已知等比数列的第m项am,公比为q,求通项公式an.
等比数列的任意一项都可以由该数列的某一项和公比表示.
两式相除得
因此
新知探究三:等比数列的通项公式
新知探究四:等比数列与函数的关系
问题6 在等差数列中,公差d ≠ 0的等差数列可以与相应的一次函数建立联系,那么对于等比数列,公比q满足什么条件的数列可以与相应的函数建立类似的联系?
指数型函数
●
●
●
●
●
l
l
问题7 类比指数函数的性质,说说公比????>0的等比数列的单调性.
?
{5940675A-B579-460E-94D1-54222C63F5DA}
0????>1
????=1
指数函数????=????????的单调性
?
等比数列????????=????????的单调性
不变
等比数列????????=????1?????????1的
单调性
????1>0
不变
????1<0
不变
{5940675A-B579-460E-94D1-54222C63F5DA}
?
不变
不变
不变
单调递减
单调递减
单调递减
单调递减
单调递增
单调递增
单调递增
单调递增
例1 若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
典例分析
①
②
②的两边分别除以①的两边,得
????2=14
?
解得
????=12或?12
?
两个????,需对其分类讨论
?
把????=12代入①,得
?
????1=384,
?
此时????5=????1????4=384×124=24
?
把????=?12代入②,得
?
????1=?384,
?
此时????5=????1????4=-384×?124=-24
?
因此,????????的第5项是24或-24
?
例1 若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
典例分析
解法2:
因为????5是????4和????6的等比中项,所以
?
因此,????????的第5项是24或-24
?
????52=????4????6=48×12=576
?
????5=±576=±24
?
所以
例2 已知等比数列{an}的公比为q,试用{an}的第m项am表示an.
等比数列{an}的通项公式:
等差数列{an}的通项公式:
典例分析
例3 数列{an}共有5项,前三项成等比数列,后三项成等差数列,第3项等于80, 第2项与第4项的和等于136,第1项与第5项的和等于132. 求这个数列.
典例分析
注意设法
(1)如果是三个数成等比数列,可设为 ,a,aq
【归纳总结】
对称设元法
(2)如果是四个数成等比数列,可设为 , ,aq,aq3
1.与等差数列有关的数的设元技巧:
2.与等比数列有关的数的设元技巧:
(1)如果是三个数成等差数列,可设为a - d,a, a+d
(2)如果是四个数成等差数列,可设为a+2d , a - d , a+d , a+2d
例题小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a1
a3
a5
a7
q
2
8
2
0.2
2. 已知{an}是一个公比为q等比数列,请在下表中的空格处填入适当的数.
3. 在等比数列{an}中,a1a3=36,a2+a4= 60. 求a1和公比q.
4
16
50
0.08
0.0032
课本P31
课堂小结
等比数列
名称
等差数列
概念
常数
通项
公式1
通项
公式2
中项
从第2项起,每一项与它前一项的差等于同一个常数
公差(d )
d 可正、可负、可零
从第2项起,每一项与它前一项的比等于同一个常数
公比(q )
q可正、可负、不可零
人教A版(2019)高中数学选择性必修二
4.3.1等比数列的概念
第二课时
一
二
三
学习目标
能在具体的问题情境中,发现数列的等比关系,并解决相应的问题.
能根据等比数列的定义推出等比数列的性质,并能运用这些性质简化运算
通过利用等比数列的相关公式解决实际应用问题,提升学生的数学建模和数学运算素养
学习目标
复习回顾
1.等比数列
2. 通项公式
4.等比数列的判断
3. 等比中项
(an)2=an-1.an+1
a,G,b成等比数列
(1) 1,2,4,8,16,…
观察下列数列,他们的单调性与公比有什么关系?
(3) 4,4,4,4,4,4,4,…
(4) 1,-1,1,-1,1,-1,1,…
公比 q=2
公比 q=
公比 q=1
公比 q=-1
问题1 可以从函数的角度,研究等比数列的单调性吗?
新知探究一:等比数列的单调性
等比数列的图象1
数列:1,2,4,8,16,…
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
●
●
●
●
●
递增数列
接下来我们再通过图象观察单调性
新知探究一:等比数列的单调性
那数列:-1,-2,-4,-8,-16,…呢?
等比数列的图象2
1
2
3
4
5
6
7
8
9
10
O
数列:
●
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
10
递减数列
新知探究一:等比数列的单调性
那数列:-8,-4,-2,-1,-12,-14…呢?
?
等比数列的图象3
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
数列:4,4,4,4,4,4,4,…
●
●
●
●
●
●
●
●
●
●
常数列
新知探究一:等比数列的单调性
等比数列的图象4
1
2
3
4
5
6
7
8
9
10
O
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
●
●
数列:1,-1,1,-1,1,-1,1,
摆动数列
-1
新知探究一:等比数列的单调性
新知探究一:等比数列的单调性
4.对于数列{an}, 若点(n, an) (n∈N*)都在函数y=cqx的图象上,其中c, q为常数,且c≠0, q≠0, q≠1,试判断数列{an}是否是等比数列,并证明你的结论.
课本P31
新知探究二:等比数列的性质
问题2 观察等比数列: 2 ,4 ,8 ,16 ,32,64,128,256,……
说出16是那两项的等比中项?并找到它们满足的规律?
思考:观察项的角标满足什么关系?由此你能得到什么固定的结论吗?
2 ,4 ,8 ,16 ,32,64,128
证明:
????????????????=????12????????+?????2
?
????s????????=????12????????+?????2
?
猜想:若{an}是公比为q的等比数列,正整数m,n,p,q满足m+n=s+t,则aman=asat.
特别地:当m+n=2k时,aman=akak=ak2
新知探究二:等比数列的性质
又m+n=s+t
即:下标和相等,对应项的积相等
(2)在有穷数列中,与首末两项“等距离”的两项之积等于首末两项的积
在等比数列{an},中公比为q
注意:等号两侧的项数必须相同
新知探究二:等比数列的性质
性质应用
∴a3a7=a2a8=9.
B
例2. 已知数列{an}为等比数列,a3=3,a11=27,求a7.
相除得q8=9.
所以q4=3,
所以a7=a3·q4
=3 · 3
=9.
练习2.等比数列{an}中,若a9=-2,则此数列前17项之积为________.
练习1.在等比数列{an}中,an>0,a2 a4+2a3a5+a4a6=36,
那么a3+a5=_______.
【解析】由题意知:
a2a4=a32,a4a6=a52
∴a32+2a3a5+a52=36,
即(a3+a5)2=36,
an>0
∴a3+a5=6
解:由题意得
a1a2a3…a15a16a17
=(a1a17)·(a2a16)·(a3a15)·…·a9
=(-2)17
=-217.
5.已知数列{an}是等比数列.
(1) a3, a5, a7是否成等比数列? 为什么? a1, a5, a9呢?
(2) 当n>1时, an-1, an, an+1是否成等比数列? 为什么?
当n>k>0时, an-k, an, an+k是等比数列吗?
课本P31
新知探究三:等比数列的判断
例题小结
例4 已知数列????????的首项????????=????.
(1)若数列????????为等差数列,公差????=2,证明数列????????????为等比数列;
(2)若数列????????为等比数列,公比????=????????,证明数列????????????????????????为等差数列.
?
分析:如何证明一个数列为等差数列或者等比数列
等差数列:
????????+?????????????=????
?
等比数列:
????????+????????????=????
?
利用定义
先求
通项公式
新知探究三:等比数列的判断
例4 已知数列????????的首项????????=????.
(1)若数列????????为等差数列,公差????=2,证明数列????????????为等比数列;
?
证明:
(1)由????1=3,????=2,得????????的通项公式为
?
????????=2????+1
?
设????????=3????????,则
?
????????+1????????=32????+332????+1=9
?
又????1=33=27
?
所以3????????是以27为首项,9为公比的等比数列
?
区分两问的求法有何不同
新知探究三:等比数列的判断
(2)由????1=3, ????=19,得????????的通项公式为
?
????????=3×19?????1=33?2????
?
????????????3????????=????????????333?2????=3?2????
?
所以????????????3????????是首项为1,公差为-2的等差数列
?
两边取以3为底的对数,得
所以????????????3????????+1?????????????3????????=3?2????+1?3?2????=?2
?
又????????????3????1=????????????33=1
?
例4 已知数列????????的首项????????=????.
(2)若数列????????为等比数列,公比????=????????,证明数列????????????????????????为等差数列.
?
新知探究三:等比数列的判断
思考 已知b>0且b≠1,如果数列{an}是等差数列,那么数列 是否一定是等比数列? 如果数列{an}是各项均为正的等比数列,那么数列{logban}是否一定是等差数列?
?
数列{an}是等差数列?数列 是等比数列.
思考 已知b>0且b≠1,如果数列{an}是等差数列,那么数列 是否一定是等比数列? 如果数列{an}是各项均为正的等比数列,那么数列{logban}是否一定是等差数列?
?
数列{an}是正项等比数列
?数列{logban}是等差数列.
2.设数列{an}, {bn}都是等比数列,分别研究下列数列是否是等比数列,若是,证明结论;若不是,请说明理由.
课本P34
新知探究三:等比数列的判断
应用小结
例5 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到?????????????)
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月初本金
月末本利和
1个月
2个月
3个月
?
?
?
12个月
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月初本金
月末本利和
1个月
2个月
3个月
12个月
????????????
?
????????????????+????.????????????%
?
????????????????+????.????????????%????
?
????????????????+????.????????????%????
?
????????????????+????.????????????%
?
????????????????+????.????????????%????
?
????????????????+????.????????????%????????
?
????????????????+????.????????????%????????
?
新知探究四:等比数列的应用
例5 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
解:
(1)设这笔钱存????个月以后的本利和组成一个数列????????,则????????是等比数列.
?
首项????1=1041+0.400%,
?
公比????=1+0.400%
?
所以,????12=1041+0.400%12≈10490.97
?
所以,12个月后的利息为10490.97-10000≈491(元)
?
利息=本利和-本金
新知探究四:等比数列的应用
设季度利率为????,这笔钱存????个季度以后的本利和组成一个数列????????,则????????也是一个等比数列,
?
解:
首项????1=1041+????,公比????=1+????
?
所以,????4=1041+????4
?
因此,以季度复利计息,存4个季度后的利息为1041+????4?104元
?
解不等式1041+????4?104≥491,得
?
????≥1.206%
?
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
?
例5 用10 000元购买某个理财产品一年.
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到?????????????)
?
新知探究四:等比数列的应用
3. 某汽车集团计划大力发展新能源汽车,2017 年全年生产新能源汽车5000辆,如果在后续的几年中,后一年新能源汽车的产量都是前一年的150%,那么2025年全年约生产新能源汽车多少辆(精确到1)?
4.某城市今年空气质量为“优”“良”的天数为105,力争2年后使空气质量为“优”“良”的天数达到240. 这个城市空气质量为“优”“良”的天数的年平均增长率应达到多少(精确到0.01)?
课本P34
例6 某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品。1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
产量
不合格率
数列????????
?
数列????????
?
等比数列
等差数列
分析:
不合格品
产量×不合格率
等差数列×等比数列
????????????????
?
新知探究四:等比数列的应用
新知探究四:等比数列的应用
解: 设从今年1月起 , 各月的产量及不合格率分别构成数列{an}, {bn}.
bn=1-[90%+0.4%(n-1)]=0.104-0.004n, 其中n=1, 2,… , 24,
则从今年1月起,各月不合格产品的数量是
anbn=1050×1.05n-1× (0.104-0.004n)
由题意,知an=1050×1.05n-1,
由计算工具计算(精确到0.1),并列表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}n
1
2
3
4
5
6
7
anbn
105.0
105.8
106.5
107.0
107.2
107.2
106.9
n
8
9
10
11
12
13
14
anbn
106.4
105.5
104.2
102.6
100.6
98.1
95.0
观察发现,数列{anbn}先递增,在第6项以后递减,所以只要设法证明当n≥6时,{anbn}递减,且a13b13<100即可.
得 n>5.
新知探究四:等比数列的应用
所以,当n≥6时,数列{anbn}递减.
又 a13b13≈98<100.
所以, 当13≤ n ≤24时,anbn ≤ a13b13<100.
所以,生产该产品一年后,月不合格的数量能控制在100个以内.
5.已知数列{an}的通项公式为 ,求使an取得最大值时n的值.
课本P34
3.等比数列的单调性
{93296810-A885-4BE3-A3E7-6D5BEEA58F35} 公比q
单调性
首项a1
q>1
0q=1
q<0
a1>0
a1<0
递增数列
递减数列
常数列
摆动数列
递减数列
递增数列
4.等比数列的项与序号的关系
{69CF1AB2-1976-4502-BF36-3FF5EA218861}两项关系
多项关系
4.3.1等比数列的概念
第一课时
一
二
三
学习目标
理解等比数列的概念
会应用定义及通项公式解决一些实际问题
学习目标
掌握等比数列的通项公式
特殊数列
等差数列
等比数列
概念
通项公式
前n项和公式
应用
数列
概念
表示
表格、图像、通项公式、递推公式
特殊化
类比
单元结构
1、等差数列:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数就叫做等差数列的公差(常用字母“d”表示).
数学表达式:
2、等差中项:
如果三个数 a,A,b 成等差数列,那么A叫做a与b的等差中项.
3、等差数列的通项公式:
( n ≥ 2,n ∈N *)
(2A= a+b )
复习回顾
新课导入
我们知道,等差数列的特征是“从第2项起,每一项与它的前一项的差都等于同一个常数” 。
类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
先从哪些方面研究呢?
新知探究一:等比数列的相关概念
实例1 两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
???????????,????????,????????,…,????????????; ①
??????????????????,????????????????,????????????????,…,????????????????????; ②
??????????,?????????,????????,…,????????????. ③
?
新知探究一:等比数列的相关概念
实例2 《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是:
????????,????????,????????,????????????,????????????,??????④
?
细菌个数
第一次
第二次
第三次
2
4
第 n 次
……
分裂次数
8
2n
实例3 在营养和生存空间没有限制的情况下,某种细菌每20 min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是:
????,????,????,????????,????????,????????,????⑤
?
新知探究一:等比数列的相关概念
新知探究一:等比数列的相关概念
实例4 某人存入银行 ɑ元钱,存期为5年,年利率是r,那么按照复利,他5年内每年末得到的本利和分别是
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息.
????(1+????),????(1+????)2,????(1+????)3,????(1+????)4,????(1+????)5. ⑥
?
问题1 请同学们仔细观察以下六个数列,类比等差数列的研究,你认为可以通过怎样的运算发现以下数列的取值规律?你发现了什么规律?
①
②
③
④
⑤
⑥
取值规律 从第 2 项起,
每一项与它的前一项的比都等于 9.
如果用 表示数列①,那么有
新知探究一:等比数列的相关概念
共同特点: 从第二项起,每一项与前一项的比都等于同一个常数.
????
?
????????????
?
????
?
????????
?
????+????
?
????
?
如果一个数列从第____项起,每一项与它的前一项的___都等于___一个常数,那么这个数列就叫做___________常数叫做等 数列的_____
公比通常用字母 q 表示
二
比
同
等比数列.
公比
如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.常数叫做等差数列的公差.
公差通常用字母d表示
比
an-an-1=d(n≥2,n∈N*)
an+1-an=d(n∈N*)
?????????????????????=????(????≠????,n≥2,n∈N*)
?
????????+????????????=????(????≠????,n∈N*)
?
等差数列的概念
等比数列的概念
问题2 类比等差数列的概念,你能抽象出等比数列的概念吗?
概念生成
符号
(1)
(3) 5,5,5,5,5,5,…
(6)
(2)
思考:观察并判断下列数列是否是等比数列,是的话,指出公比,不是的话请说明理由:
(4) 0,1,2,4,8,…
(5) 2,0,2,0,2,…
是,公比是 2
是,公比是 -2
是,公比是 1
不一定,分类讨论
不是,分母不能为 0
不是,公比不能是 0
概念辨析
1. 判断下列数列是否是等差数列. 如果是,写出它的公差.
课本P31
追问1:等差数列的项、公差均可以是0吗?等比数列呢?
追问2:常数列是等差数列吗?是等比数列吗?
追问3:是否存在既是等差数列又是等比数列的数列?
常数列一定是等差数列,公差为0;
非零常数列是等比数列,公比为1.
非零常数列既是等差数列又是等比数列,公差为0,公比为1.
等差数列的项、公差均可以是0,但等比数列的项和公比均不可以是0
概念辨析
等差中项
等比中项
如果三个数a,A,b组成等差数列,那么A叫做a和b的等差中项.
如果三个数a,G,b组成等比数列,那么G叫做a和b的等比中项
定义
a,A,b成等差数列
a,G,b成等比数列
关系
追问:任意两个实数a,b都有等比中项吗?
若a,b同号则有两个等比中项;若a,b异号则无等比中项.
新知探究二:等比中项
问题3 类比等差中项的概念,你能抽象出等比中项的概念吗?
∴a, G, b成等比数列
?
(ab>0)
新知探究三:等比数列的通项公式
问题4 你能类比等差数列的通项公式推导,根据等比数列的定义及递推公式推导它的通项公式吗?怎么推?
等差数列
类比
法一:不完全归纳法
……
由此归纳等比数列的通项公式可得:
等比数列
新知探究三:等比数列的通项公式
问题4 你能类比等差数列的通项公式推导,根据等比数列的定义及递推公式推导它的通项公式吗?怎么推?
法二:累加法
……
+)
等差数列
类比
……
由等比数列的定义 ?????????????????????=????(????≥????,????∈?????)得
?
n-1个
又a1=a1q0=a1q1-1,即当n=1时上式也成立.
an=a1qn-1 (n∈ ?????)
?
累乘法
等比数列的通项公式:
问题5 已知等比数列的第m项am,公比为q,求通项公式an.
等比数列的任意一项都可以由该数列的某一项和公比表示.
两式相除得
因此
新知探究三:等比数列的通项公式
新知探究四:等比数列与函数的关系
问题6 在等差数列中,公差d ≠ 0的等差数列可以与相应的一次函数建立联系,那么对于等比数列,公比q满足什么条件的数列可以与相应的函数建立类似的联系?
指数型函数
●
●
●
●
●
l
l
问题7 类比指数函数的性质,说说公比????>0的等比数列的单调性.
?
{5940675A-B579-460E-94D1-54222C63F5DA}
0????>1
????=1
指数函数????=????????的单调性
?
等比数列????????=????????的单调性
不变
等比数列????????=????1?????????1的
单调性
????1>0
不变
????1<0
不变
{5940675A-B579-460E-94D1-54222C63F5DA}
?
不变
不变
不变
单调递减
单调递减
单调递减
单调递减
单调递增
单调递增
单调递增
单调递增
例1 若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
典例分析
①
②
②的两边分别除以①的两边,得
????2=14
?
解得
????=12或?12
?
两个????,需对其分类讨论
?
把????=12代入①,得
?
????1=384,
?
此时????5=????1????4=384×124=24
?
把????=?12代入②,得
?
????1=?384,
?
此时????5=????1????4=-384×?124=-24
?
因此,????????的第5项是24或-24
?
例1 若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
典例分析
解法2:
因为????5是????4和????6的等比中项,所以
?
因此,????????的第5项是24或-24
?
????52=????4????6=48×12=576
?
????5=±576=±24
?
所以
例2 已知等比数列{an}的公比为q,试用{an}的第m项am表示an.
等比数列{an}的通项公式:
等差数列{an}的通项公式:
典例分析
例3 数列{an}共有5项,前三项成等比数列,后三项成等差数列,第3项等于80, 第2项与第4项的和等于136,第1项与第5项的和等于132. 求这个数列.
典例分析
注意设法
(1)如果是三个数成等比数列,可设为 ,a,aq
【归纳总结】
对称设元法
(2)如果是四个数成等比数列,可设为 , ,aq,aq3
1.与等差数列有关的数的设元技巧:
2.与等比数列有关的数的设元技巧:
(1)如果是三个数成等差数列,可设为a - d,a, a+d
(2)如果是四个数成等差数列,可设为a+2d , a - d , a+d , a+2d
例题小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a1
a3
a5
a7
q
2
8
2
0.2
2. 已知{an}是一个公比为q等比数列,请在下表中的空格处填入适当的数.
3. 在等比数列{an}中,a1a3=36,a2+a4= 60. 求a1和公比q.
4
16
50
0.08
0.0032
课本P31
课堂小结
等比数列
名称
等差数列
概念
常数
通项
公式1
通项
公式2
中项
从第2项起,每一项与它前一项的差等于同一个常数
公差(d )
d 可正、可负、可零
从第2项起,每一项与它前一项的比等于同一个常数
公比(q )
q可正、可负、不可零
人教A版(2019)高中数学选择性必修二
4.3.1等比数列的概念
第二课时
一
二
三
学习目标
能在具体的问题情境中,发现数列的等比关系,并解决相应的问题.
能根据等比数列的定义推出等比数列的性质,并能运用这些性质简化运算
通过利用等比数列的相关公式解决实际应用问题,提升学生的数学建模和数学运算素养
学习目标
复习回顾
1.等比数列
2. 通项公式
4.等比数列的判断
3. 等比中项
(an)2=an-1.an+1
a,G,b成等比数列
(1) 1,2,4,8,16,…
观察下列数列,他们的单调性与公比有什么关系?
(3) 4,4,4,4,4,4,4,…
(4) 1,-1,1,-1,1,-1,1,…
公比 q=2
公比 q=
公比 q=1
公比 q=-1
问题1 可以从函数的角度,研究等比数列的单调性吗?
新知探究一:等比数列的单调性
等比数列的图象1
数列:1,2,4,8,16,…
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
●
●
●
●
●
递增数列
接下来我们再通过图象观察单调性
新知探究一:等比数列的单调性
那数列:-1,-2,-4,-8,-16,…呢?
等比数列的图象2
1
2
3
4
5
6
7
8
9
10
O
数列:
●
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
10
递减数列
新知探究一:等比数列的单调性
那数列:-8,-4,-2,-1,-12,-14…呢?
?
等比数列的图象3
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
数列:4,4,4,4,4,4,4,…
●
●
●
●
●
●
●
●
●
●
常数列
新知探究一:等比数列的单调性
等比数列的图象4
1
2
3
4
5
6
7
8
9
10
O
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
●
●
数列:1,-1,1,-1,1,-1,1,
摆动数列
-1
新知探究一:等比数列的单调性
新知探究一:等比数列的单调性
4.对于数列{an}, 若点(n, an) (n∈N*)都在函数y=cqx的图象上,其中c, q为常数,且c≠0, q≠0, q≠1,试判断数列{an}是否是等比数列,并证明你的结论.
课本P31
新知探究二:等比数列的性质
问题2 观察等比数列: 2 ,4 ,8 ,16 ,32,64,128,256,……
说出16是那两项的等比中项?并找到它们满足的规律?
思考:观察项的角标满足什么关系?由此你能得到什么固定的结论吗?
2 ,4 ,8 ,16 ,32,64,128
证明:
????????????????=????12????????+?????2
?
????s????????=????12????????+?????2
?
猜想:若{an}是公比为q的等比数列,正整数m,n,p,q满足m+n=s+t,则aman=asat.
特别地:当m+n=2k时,aman=akak=ak2
新知探究二:等比数列的性质
又m+n=s+t
即:下标和相等,对应项的积相等
(2)在有穷数列中,与首末两项“等距离”的两项之积等于首末两项的积
在等比数列{an},中公比为q
注意:等号两侧的项数必须相同
新知探究二:等比数列的性质
性质应用
∴a3a7=a2a8=9.
B
例2. 已知数列{an}为等比数列,a3=3,a11=27,求a7.
相除得q8=9.
所以q4=3,
所以a7=a3·q4
=3 · 3
=9.
练习2.等比数列{an}中,若a9=-2,则此数列前17项之积为________.
练习1.在等比数列{an}中,an>0,a2 a4+2a3a5+a4a6=36,
那么a3+a5=_______.
【解析】由题意知:
a2a4=a32,a4a6=a52
∴a32+2a3a5+a52=36,
即(a3+a5)2=36,
an>0
∴a3+a5=6
解:由题意得
a1a2a3…a15a16a17
=(a1a17)·(a2a16)·(a3a15)·…·a9
=(-2)17
=-217.
5.已知数列{an}是等比数列.
(1) a3, a5, a7是否成等比数列? 为什么? a1, a5, a9呢?
(2) 当n>1时, an-1, an, an+1是否成等比数列? 为什么?
当n>k>0时, an-k, an, an+k是等比数列吗?
课本P31
新知探究三:等比数列的判断
例题小结
例4 已知数列????????的首项????????=????.
(1)若数列????????为等差数列,公差????=2,证明数列????????????为等比数列;
(2)若数列????????为等比数列,公比????=????????,证明数列????????????????????????为等差数列.
?
分析:如何证明一个数列为等差数列或者等比数列
等差数列:
????????+?????????????=????
?
等比数列:
????????+????????????=????
?
利用定义
先求
通项公式
新知探究三:等比数列的判断
例4 已知数列????????的首项????????=????.
(1)若数列????????为等差数列,公差????=2,证明数列????????????为等比数列;
?
证明:
(1)由????1=3,????=2,得????????的通项公式为
?
????????=2????+1
?
设????????=3????????,则
?
????????+1????????=32????+332????+1=9
?
又????1=33=27
?
所以3????????是以27为首项,9为公比的等比数列
?
区分两问的求法有何不同
新知探究三:等比数列的判断
(2)由????1=3, ????=19,得????????的通项公式为
?
????????=3×19?????1=33?2????
?
????????????3????????=????????????333?2????=3?2????
?
所以????????????3????????是首项为1,公差为-2的等差数列
?
两边取以3为底的对数,得
所以????????????3????????+1?????????????3????????=3?2????+1?3?2????=?2
?
又????????????3????1=????????????33=1
?
例4 已知数列????????的首项????????=????.
(2)若数列????????为等比数列,公比????=????????,证明数列????????????????????????为等差数列.
?
新知探究三:等比数列的判断
思考 已知b>0且b≠1,如果数列{an}是等差数列,那么数列 是否一定是等比数列? 如果数列{an}是各项均为正的等比数列,那么数列{logban}是否一定是等差数列?
?
数列{an}是等差数列?数列 是等比数列.
思考 已知b>0且b≠1,如果数列{an}是等差数列,那么数列 是否一定是等比数列? 如果数列{an}是各项均为正的等比数列,那么数列{logban}是否一定是等差数列?
?
数列{an}是正项等比数列
?数列{logban}是等差数列.
2.设数列{an}, {bn}都是等比数列,分别研究下列数列是否是等比数列,若是,证明结论;若不是,请说明理由.
课本P34
新知探究三:等比数列的判断
应用小结
例5 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到?????????????)
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月初本金
月末本利和
1个月
2个月
3个月
?
?
?
12个月
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月初本金
月末本利和
1个月
2个月
3个月
12个月
????????????
?
????????????????+????.????????????%
?
????????????????+????.????????????%????
?
????????????????+????.????????????%????
?
????????????????+????.????????????%
?
????????????????+????.????????????%????
?
????????????????+????.????????????%????????
?
????????????????+????.????????????%????????
?
新知探究四:等比数列的应用
例5 用10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获利多少利息(精确到1元)?
解:
(1)设这笔钱存????个月以后的本利和组成一个数列????????,则????????是等比数列.
?
首项????1=1041+0.400%,
?
公比????=1+0.400%
?
所以,????12=1041+0.400%12≈10490.97
?
所以,12个月后的利息为10490.97-10000≈491(元)
?
利息=本利和-本金
新知探究四:等比数列的应用
设季度利率为????,这笔钱存????个季度以后的本利和组成一个数列????????,则????????也是一个等比数列,
?
解:
首项????1=1041+????,公比????=1+????
?
所以,????4=1041+????4
?
因此,以季度复利计息,存4个季度后的利息为1041+????4?104元
?
解不等式1041+????4?104≥491,得
?
????≥1.206%
?
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
?
例5 用10 000元购买某个理财产品一年.
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息.(精确到?????????????)
?
新知探究四:等比数列的应用
3. 某汽车集团计划大力发展新能源汽车,2017 年全年生产新能源汽车5000辆,如果在后续的几年中,后一年新能源汽车的产量都是前一年的150%,那么2025年全年约生产新能源汽车多少辆(精确到1)?
4.某城市今年空气质量为“优”“良”的天数为105,力争2年后使空气质量为“优”“良”的天数达到240. 这个城市空气质量为“优”“良”的天数的年平均增长率应达到多少(精确到0.01)?
课本P34
例6 某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品。1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
产量
不合格率
数列????????
?
数列????????
?
等比数列
等差数列
分析:
不合格品
产量×不合格率
等差数列×等比数列
????????????????
?
新知探究四:等比数列的应用
新知探究四:等比数列的应用
解: 设从今年1月起 , 各月的产量及不合格率分别构成数列{an}, {bn}.
bn=1-[90%+0.4%(n-1)]=0.104-0.004n, 其中n=1, 2,… , 24,
则从今年1月起,各月不合格产品的数量是
anbn=1050×1.05n-1× (0.104-0.004n)
由题意,知an=1050×1.05n-1,
由计算工具计算(精确到0.1),并列表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}n
1
2
3
4
5
6
7
anbn
105.0
105.8
106.5
107.0
107.2
107.2
106.9
n
8
9
10
11
12
13
14
anbn
106.4
105.5
104.2
102.6
100.6
98.1
95.0
观察发现,数列{anbn}先递增,在第6项以后递减,所以只要设法证明当n≥6时,{anbn}递减,且a13b13<100即可.
得 n>5.
新知探究四:等比数列的应用
所以,当n≥6时,数列{anbn}递减.
又 a13b13≈98<100.
所以, 当13≤ n ≤24时,anbn ≤ a13b13<100.
所以,生产该产品一年后,月不合格的数量能控制在100个以内.
5.已知数列{an}的通项公式为 ,求使an取得最大值时n的值.
课本P34
3.等比数列的单调性
{93296810-A885-4BE3-A3E7-6D5BEEA58F35} 公比q
单调性
首项a1
q>1
0
q<0
a1>0
a1<0
递增数列
递减数列
常数列
摆动数列
递减数列
递增数列
4.等比数列的项与序号的关系
{69CF1AB2-1976-4502-BF36-3FF5EA218861}两项关系
多项关系
