人教A版(2019)选择性必修第二册 4.2.2等差数列的前n项和公式(共2课时)课件(共38张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册 4.2.2等差数列的前n项和公式(共2课时)课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 00:00:00 | ||
图片预览










文档简介
人教A版(2019)高中数学选择性必修二
4.2.2等差数列的前n项和公式
第一课时
一
二
三
学习目标
理解公式的推导方法
能较熟练应用等差数列前n项和公式求和
学习目标
掌握等差数列前n项和公式
复习回顾
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
3. 几种计算公差d的方法:
4. 等差中项
m+n=p+q ? am+an=ap+aq .
5. 等差数列的性质
?A=????+?????2
?
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+---+99+100=?
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面 的方法迅速算出了正确答案:
情境导入
1+2+3+…+50+51+…+98+99+100=
5050
50对
101
101
101
101
新知探究一:等差数列的前n项和公式
问题1:计算
新知探究一:等差数列的前n项和公式
高斯的算法实际上解决了求等差数列
1,2,3,???,n,??? ①
前100项的和的问题.
思考 你能说说高斯在求和过程中利用了数列①的什么性质吗?你能从中得到求数列①的前n项和的方法吗?
对于数列1,2,3,???,n,??? ,若设an=n,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了 这一特殊关系.
这里用到了数列的性质:若p+q=s+t,则ap+ aq=as+ at,它使不同数的求和问题转化成了相同数(即101)的求和,从而简化了运算.
动脑思考 探究新知
配对
问题2:
偶数项
奇数项
问题1:
问题3:
思路2(拿出中间项,再首尾配对) 原式=(1+101)+ (2+100)+ (3+99)+… + (50+52)+51
思路1(拿出末项,再首尾配对)原式=(1+2+3+… + 100)+101
思路3(先凑成偶数项,再配对)原式=(1+2+3+… + 100+102)-102
思路4(先凑成偶数项,再配对)原式=0+1+2+3+… + 100+101
将上述方法推广到一般,可以得到:
于是有
当n是偶数时,有
当n是奇数时,有
∴对任意正整数n,都有
问题3: 你能用高斯的方法计算1+2+3+… +n吗?
新知探究一:等差数列的前n项和公式
思考 我们发现,在求前n个正整数的和时,要对n分奇数、偶数进行讨论,比较麻烦. 能否设法避免分类讨论?
这种求和方法叫倒序求和法
性质:如果数列{an} 是等差数列,p,q,s,t∈N*,
且 p+q=s+t,则 ap+aq=as+at
左右两边分别相加
n个
①
②
新知探究一:等差数列的前n项和公式
问题4 那么,对于一般的等差数列,如何求它的前n项和呢?
这就是等差数列前n项和的公式!
等差数列前n项和公式
请记住我
项数
首项
末项
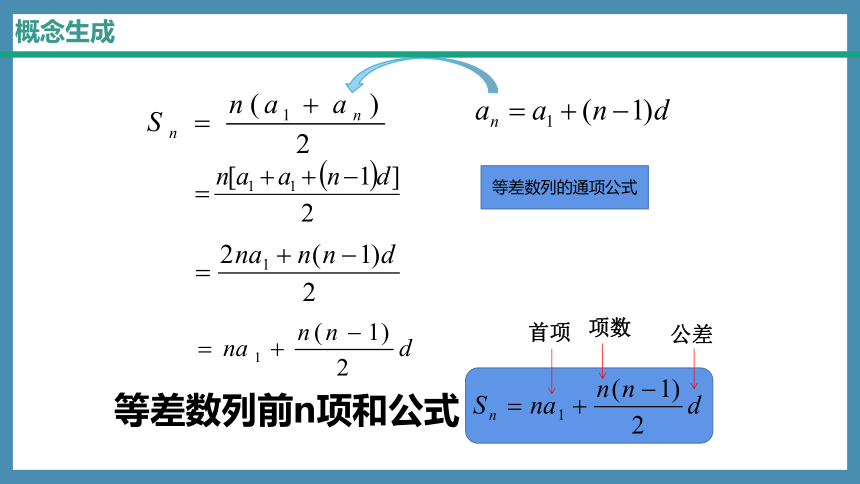
概念生成
等差数列的通项公式
等差数列前n项和公式
首项
项数
公差
概念生成
等差数列{an}的相关公式及性质:
1.等差数列{an}的通项公式:
2.等差数列{an}的前n项和公式:
3.等差数列{an}的重要性质:
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
例6 已知数列{an}是等差数列.
例7 已知一个等 差数列{an}前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗?
根据下列各题中的条件,求相应等差数列{an }的前n项和Sn .
(1) a1=5, an=95, n=10; (2) a1=100, d=-2, n=50;
(3) a1=-4, a8=-18, n=10; (4) a1=14.5, d=0.7, an=32.
课本P22
根据下列各题中的条件,求相应等差数列{an }的前n项和Sn .
(1) a1=5, an=95, n=10; (2) a1=100, d=-2, n=50;
(3) a1=-4, a8=-18, n=10; (4) a1=14.5, d=0.7, an=32.
课本P22
2. 等差数列-1, -3, -5, ???的前多少项的 和是-100 ?
3. 在等差数列{an}中,Sn为其前n项的和,若S4=6,S8=20,求S16 .
课本P23
4. 在等差数列{an}中,若S15=5(a2+a6+ak),求k.
课本P23
等差数列的前n项和公式:
形式1:
形式2:
课堂小结
(1) an=a1+(n-1)d (n≥1).
等差数列通项公式:
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
人教A版(2019)高中数学选择性必修二
4.2.2等差数列的前n项和公式
第二课时
一
二
三
学习目标
掌握等差数列前n项和的应用
能较熟练应用等差数列前n项和公式求和
学习目标
会求等差数列前n项和的最值
等差数列的前n项和公式:
形式1:
形式2:
复习回顾
(1) an=a1+(n-1)d (n≥1).
等差数列通项公式:
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
新知探究一:等差数列的前n项和公式的应用
例1 某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多2个座位.问第1排应安排多少个座位?
分析:将第1排到第20排的座位数依次排成一列,构成数列{an} ,设数列{an} 的前n项和为????????。由题意可知, {an}是等差数列,且公差及前20项和已知,所以可利用等差数列的前n项和公式求首项。
?
1.本题属于与等差数列前n项和有关的应用题,其关键在于构造合适的等差数列.
2.遇到与正整数有关的应用题时,可以考虑与数列知识联系,建立数列模型,具体解决要注意以下两点:
(1)抓住实际问题的特征,明确是什么类型的数列模型.
(2)深入分析题意,确定是求通项公式an,或是求前n项和Sn,还是求项数n.
例题小结
1. 某市一家商场的新年最高促销奖设立了两种领奖方式:第一种,获奖者可以选择2000元的奖金;第二种,从12月20日到第二年的1月1日,每天到该商场领取奖品,第1天领取的奖品价值为100元,第2天为110元,以后逐天增加10元. 你认为哪种领奖方式获奖者受益更多?
课本P24
新知探究二:等差数列的前n项和的最值
例9 已 知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值? 若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
分析1:由????????>????和????< ????,可以证明{????????}是递减数列,且存在正整数????,使得当
????≥????时,?????????
通项公式法求最值
解法1:
注意:当数列的项中有数值为0时,n应有两解.
新知探究二:等差数列的前n项和的最值
分析????:另一方面,等差数列的前n项和公式可写成??????????=????2?????2+????1?????2????,
所以当????≠0时, ????????可以看成二次函数????=????2?????2+????1?????2????(????∈????),
当????= ????时函数值。如图,当????< 0时, ????????关于????的图像是一条开口向下
的抛物线上的一些点,因此,可以利用二次函数求相应的????, ????????的值。
?
前n项和公式法求最值
解法2:
例题小结
求等差数列的前n项和最值的两种常用方法
方法一:通项公式法求最值
情形1:当a1>0,d<0时,
数列前面有若干项为正, 此时所有非负项的和为Sn的最大值.
此时由an≥0且an+1≤0求n的值
情形2: 当a1<0,d>0时,
数列前面有若干项为负, 此时所有非正项的和为Sn的最小值.
此时由an≤0 且an+1 ≥ 0求n的值
方法二:前n项和公式法求最值
例题小结
思考:我们发现,等差数列{an}的前n项和公式 可化简为 , 这个函数式与函数 有什么关系?
当d=0 时,Sn的图象是一条直线上的均匀分布的点.
当d≠0 时, 是二次函数
当x = n时的函数值.
几何意义:前n项和公式Sn的图象是一条过坐标原点的抛物线上孤立的点.
常数列
例题小结
情形1:当a1>0,d<0 时,Sn的图象是一条开口向下的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
情形2:当a1<0,d>0 时,Sn的图象是一条开口向上的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法1
由S3=S11得
∴ d=-2
∴当n=7时,Sn取最大值49.
7
n
11
3
Sn
巩固练习
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法2
由S3=S11得
d=-2<0
∴当n=7时,Sn取最大值49.
则Sn的图象如图所示
又S3=S11
所以图象的对称轴为
7
n
11
3
Sn
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法3
由S3=S11得
d=-2
∴当n=7时,Sn取最大值49.
∴ an=13+(n-1) ×(-2)=-2n+15
由
得
∴a7+a8=0
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法4
由S3=S11得
∴当n=7时,Sn取最大值49.
a4+a5+a6+……+a11=0
而 a4+a11=a5+a10=a6+a9=a7+a8
又d=-2<0,a1=13>0
∴a7>0,a8<0
当堂达标
解析∵S6>S7,∴a7<0,∵S7>S5,∴a6+a7>0,∴a6>0,∴d<0,A正确.
AB
又S11=????????????(a1+a11)=11a6>0,B正确.
?
S12=????????????(a1+a12)=6(a6+a7)>0,C不正确.
?
{Sn}中最大项为S6,D不正确.
3. 已知等差数列-4.2,-3.7,-3.2,???的前n项和为Sn,Sn是否存在最大(小)值? 如果存在,求出取得最值时n的值.
课本P24
(1)当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值. 此时由an≥0且an+1≤0求n的值;
(2)当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值. 此时由an≤0 且an+1 ≥ 0求n的值;
注意:当数列的项中有数值为0时,n应有两解.
求等差数列{an}的前n项和Sn的最值的方法
1.前n项和公式法
2.通项公式法
利用Sn=An2+Bn进行配方,求二次函数的最值,
此时n应取最接近????????????? 的正整数值;
?
利用等差数列的增减性及an的符号变化
课堂小结
4.2.2等差数列的前n项和公式
第一课时
一
二
三
学习目标
理解公式的推导方法
能较熟练应用等差数列前n项和公式求和
学习目标
掌握等差数列前n项和公式
复习回顾
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
3. 几种计算公差d的方法:
4. 等差中项
m+n=p+q ? am+an=ap+aq .
5. 等差数列的性质
?A=????+?????2
?
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+---+99+100=?
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面 的方法迅速算出了正确答案:
情境导入
1+2+3+…+50+51+…+98+99+100=
5050
50对
101
101
101
101
新知探究一:等差数列的前n项和公式
问题1:计算
新知探究一:等差数列的前n项和公式
高斯的算法实际上解决了求等差数列
1,2,3,???,n,??? ①
前100项的和的问题.
思考 你能说说高斯在求和过程中利用了数列①的什么性质吗?你能从中得到求数列①的前n项和的方法吗?
对于数列1,2,3,???,n,??? ,若设an=n,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了 这一特殊关系.
这里用到了数列的性质:若p+q=s+t,则ap+ aq=as+ at,它使不同数的求和问题转化成了相同数(即101)的求和,从而简化了运算.
动脑思考 探究新知
配对
问题2:
偶数项
奇数项
问题1:
问题3:
思路2(拿出中间项,再首尾配对) 原式=(1+101)+ (2+100)+ (3+99)+… + (50+52)+51
思路1(拿出末项,再首尾配对)原式=(1+2+3+… + 100)+101
思路3(先凑成偶数项,再配对)原式=(1+2+3+… + 100+102)-102
思路4(先凑成偶数项,再配对)原式=0+1+2+3+… + 100+101
将上述方法推广到一般,可以得到:
于是有
当n是偶数时,有
当n是奇数时,有
∴对任意正整数n,都有
问题3: 你能用高斯的方法计算1+2+3+… +n吗?
新知探究一:等差数列的前n项和公式
思考 我们发现,在求前n个正整数的和时,要对n分奇数、偶数进行讨论,比较麻烦. 能否设法避免分类讨论?
这种求和方法叫倒序求和法
性质:如果数列{an} 是等差数列,p,q,s,t∈N*,
且 p+q=s+t,则 ap+aq=as+at
左右两边分别相加
n个
①
②
新知探究一:等差数列的前n项和公式
问题4 那么,对于一般的等差数列,如何求它的前n项和呢?
这就是等差数列前n项和的公式!
等差数列前n项和公式
请记住我
项数
首项
末项
概念生成
等差数列的通项公式
等差数列前n项和公式
首项
项数
公差
概念生成
等差数列{an}的相关公式及性质:
1.等差数列{an}的通项公式:
2.等差数列{an}的前n项和公式:
3.等差数列{an}的重要性质:
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
例6 已知数列{an}是等差数列.
例7 已知一个等 差数列{an}前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗?
根据下列各题中的条件,求相应等差数列{an }的前n项和Sn .
(1) a1=5, an=95, n=10; (2) a1=100, d=-2, n=50;
(3) a1=-4, a8=-18, n=10; (4) a1=14.5, d=0.7, an=32.
课本P22
根据下列各题中的条件,求相应等差数列{an }的前n项和Sn .
(1) a1=5, an=95, n=10; (2) a1=100, d=-2, n=50;
(3) a1=-4, a8=-18, n=10; (4) a1=14.5, d=0.7, an=32.
课本P22
2. 等差数列-1, -3, -5, ???的前多少项的 和是-100 ?
3. 在等差数列{an}中,Sn为其前n项的和,若S4=6,S8=20,求S16 .
课本P23
4. 在等差数列{an}中,若S15=5(a2+a6+ak),求k.
课本P23
等差数列的前n项和公式:
形式1:
形式2:
课堂小结
(1) an=a1+(n-1)d (n≥1).
等差数列通项公式:
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
人教A版(2019)高中数学选择性必修二
4.2.2等差数列的前n项和公式
第二课时
一
二
三
学习目标
掌握等差数列前n项和的应用
能较熟练应用等差数列前n项和公式求和
学习目标
会求等差数列前n项和的最值
等差数列的前n项和公式:
形式1:
形式2:
复习回顾
(1) an=a1+(n-1)d (n≥1).
等差数列通项公式:
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
新知探究一:等差数列的前n项和公式的应用
例1 某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多2个座位.问第1排应安排多少个座位?
分析:将第1排到第20排的座位数依次排成一列,构成数列{an} ,设数列{an} 的前n项和为????????。由题意可知, {an}是等差数列,且公差及前20项和已知,所以可利用等差数列的前n项和公式求首项。
?
1.本题属于与等差数列前n项和有关的应用题,其关键在于构造合适的等差数列.
2.遇到与正整数有关的应用题时,可以考虑与数列知识联系,建立数列模型,具体解决要注意以下两点:
(1)抓住实际问题的特征,明确是什么类型的数列模型.
(2)深入分析题意,确定是求通项公式an,或是求前n项和Sn,还是求项数n.
例题小结
1. 某市一家商场的新年最高促销奖设立了两种领奖方式:第一种,获奖者可以选择2000元的奖金;第二种,从12月20日到第二年的1月1日,每天到该商场领取奖品,第1天领取的奖品价值为100元,第2天为110元,以后逐天增加10元. 你认为哪种领奖方式获奖者受益更多?
课本P24
新知探究二:等差数列的前n项和的最值
例9 已 知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值? 若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
分析1:由????????>????和????< ????,可以证明{????????}是递减数列,且存在正整数????,使得当
????≥????时,?????????
通项公式法求最值
解法1:
注意:当数列的项中有数值为0时,n应有两解.
新知探究二:等差数列的前n项和的最值
分析????:另一方面,等差数列的前n项和公式可写成??????????=????2?????2+????1?????2????,
所以当????≠0时, ????????可以看成二次函数????=????2?????2+????1?????2????(????∈????),
当????= ????时函数值。如图,当????< 0时, ????????关于????的图像是一条开口向下
的抛物线上的一些点,因此,可以利用二次函数求相应的????, ????????的值。
?
前n项和公式法求最值
解法2:
例题小结
求等差数列的前n项和最值的两种常用方法
方法一:通项公式法求最值
情形1:当a1>0,d<0时,
数列前面有若干项为正, 此时所有非负项的和为Sn的最大值.
此时由an≥0且an+1≤0求n的值
情形2: 当a1<0,d>0时,
数列前面有若干项为负, 此时所有非正项的和为Sn的最小值.
此时由an≤0 且an+1 ≥ 0求n的值
方法二:前n项和公式法求最值
例题小结
思考:我们发现,等差数列{an}的前n项和公式 可化简为 , 这个函数式与函数 有什么关系?
当d=0 时,Sn的图象是一条直线上的均匀分布的点.
当d≠0 时, 是二次函数
当x = n时的函数值.
几何意义:前n项和公式Sn的图象是一条过坐标原点的抛物线上孤立的点.
常数列
例题小结
情形1:当a1>0,d<0 时,Sn的图象是一条开口向下的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
情形2:当a1<0,d>0 时,Sn的图象是一条开口向上的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法1
由S3=S11得
∴ d=-2
∴当n=7时,Sn取最大值49.
7
n
11
3
Sn
巩固练习
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法2
由S3=S11得
d=-2<0
∴当n=7时,Sn取最大值49.
则Sn的图象如图所示
又S3=S11
所以图象的对称轴为
7
n
11
3
Sn
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法3
由S3=S11得
d=-2
∴当n=7时,Sn取最大值49.
∴ an=13+(n-1) ×(-2)=-2n+15
由
得
∴a7+a8=0
练习1:已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法4
由S3=S11得
∴当n=7时,Sn取最大值49.
a4+a5+a6+……+a11=0
而 a4+a11=a5+a10=a6+a9=a7+a8
又d=-2<0,a1=13>0
∴a7>0,a8<0
当堂达标
解析∵S6>S7,∴a7<0,∵S7>S5,∴a6+a7>0,∴a6>0,∴d<0,A正确.
AB
又S11=????????????(a1+a11)=11a6>0,B正确.
?
S12=????????????(a1+a12)=6(a6+a7)>0,C不正确.
?
{Sn}中最大项为S6,D不正确.
3. 已知等差数列-4.2,-3.7,-3.2,???的前n项和为Sn,Sn是否存在最大(小)值? 如果存在,求出取得最值时n的值.
课本P24
(1)当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值. 此时由an≥0且an+1≤0求n的值;
(2)当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值. 此时由an≤0 且an+1 ≥ 0求n的值;
注意:当数列的项中有数值为0时,n应有两解.
求等差数列{an}的前n项和Sn的最值的方法
1.前n项和公式法
2.通项公式法
利用Sn=An2+Bn进行配方,求二次函数的最值,
此时n应取最接近????????????? 的正整数值;
?
利用等差数列的增减性及an的符号变化
课堂小结
