展开与折叠(黑龙江省大庆市)

课件39张PPT。展开与折叠想一想:
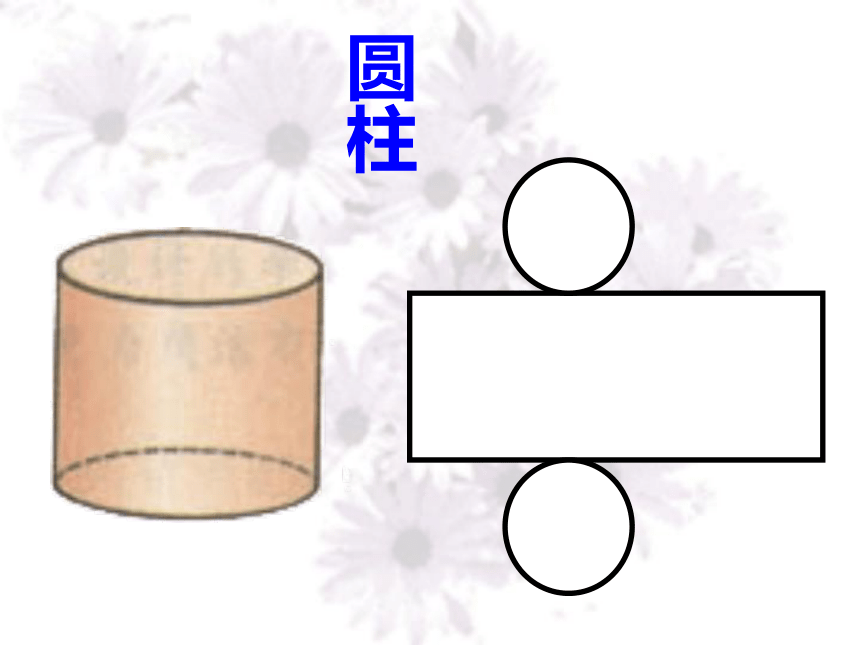
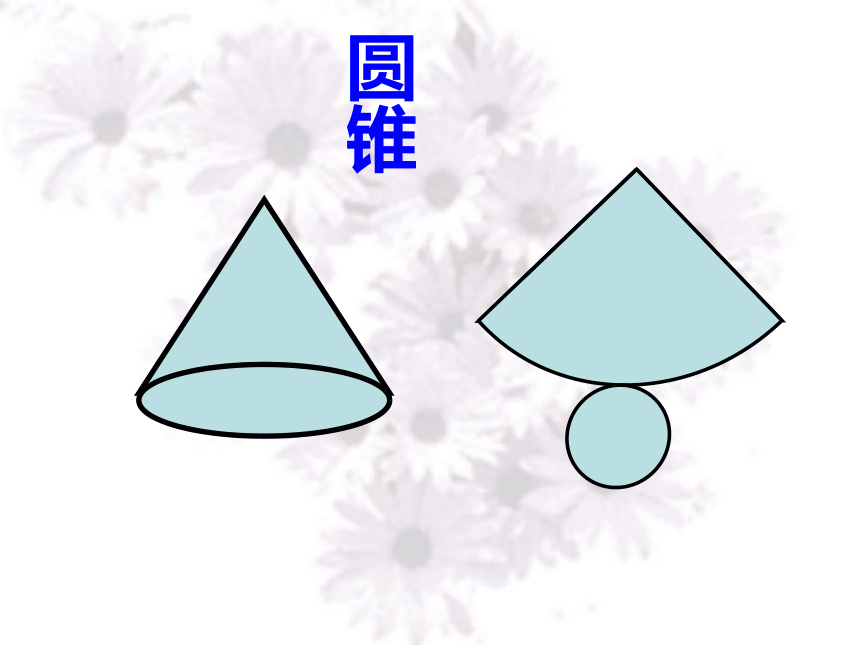
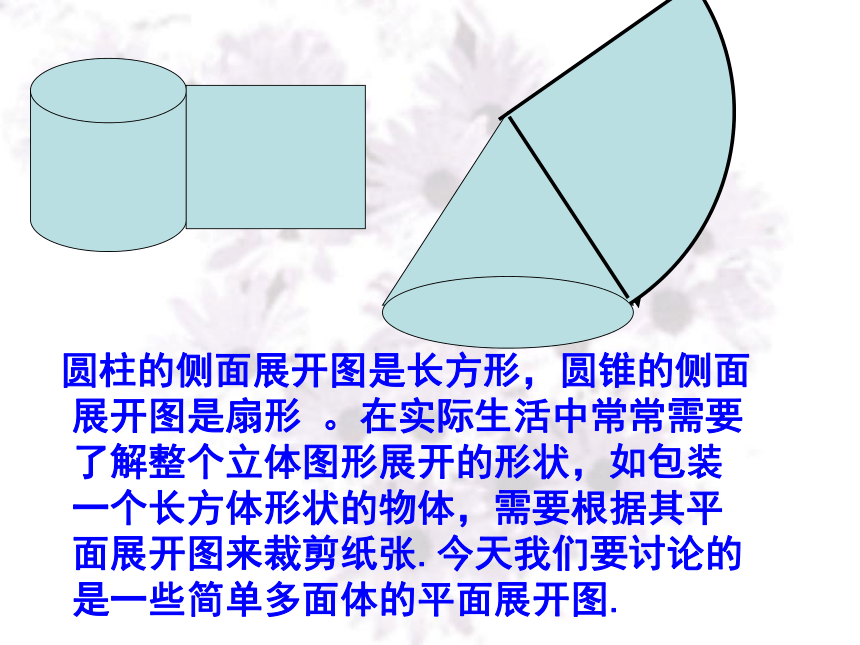
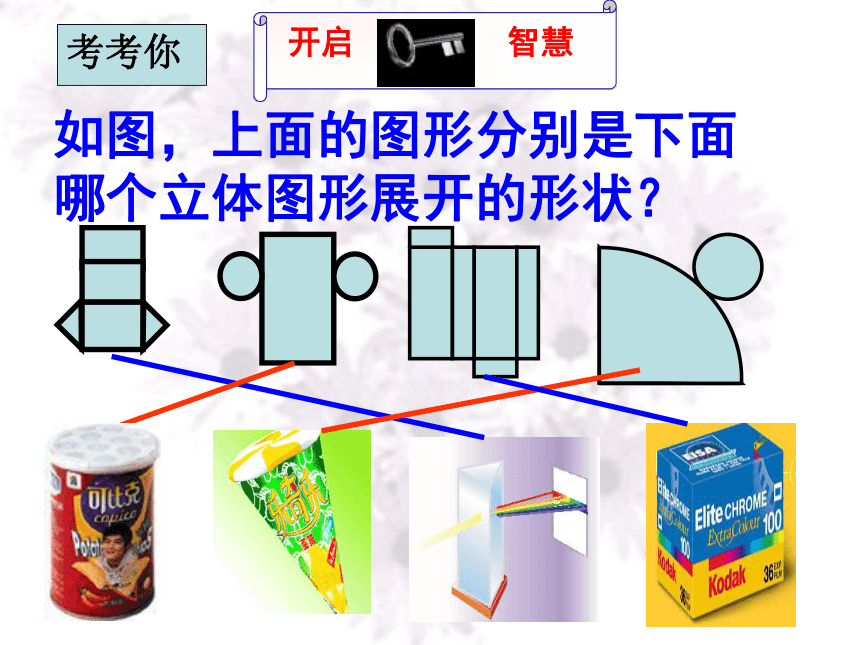
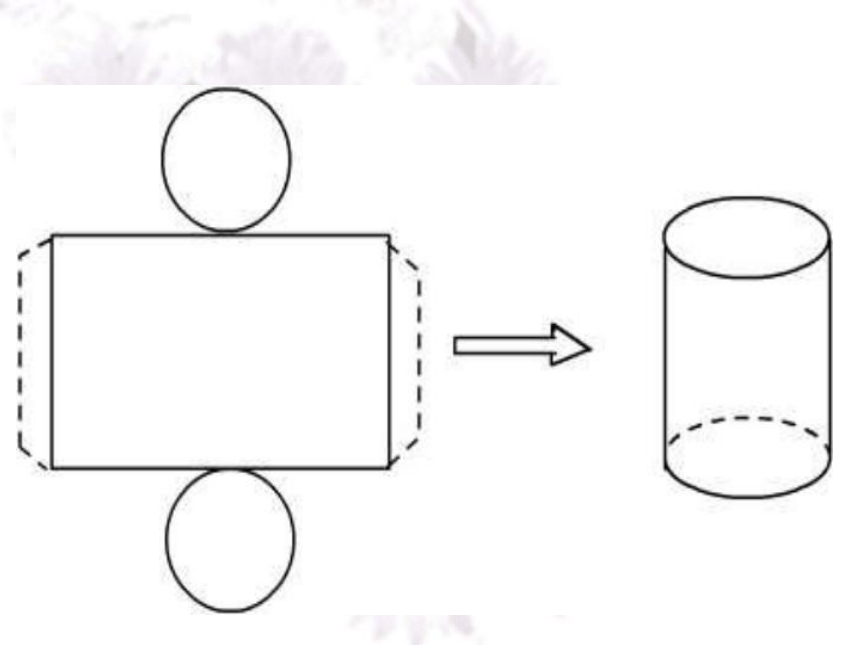
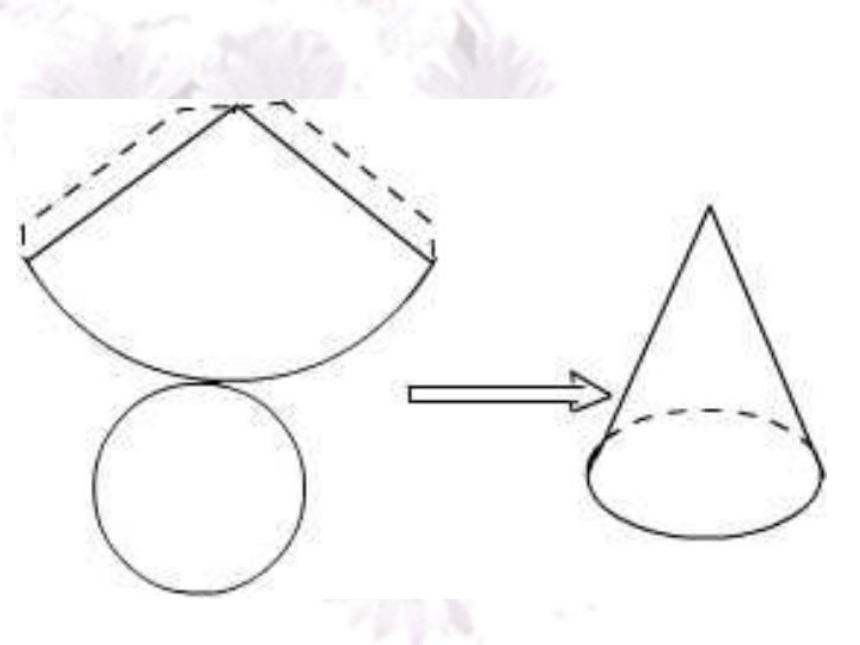
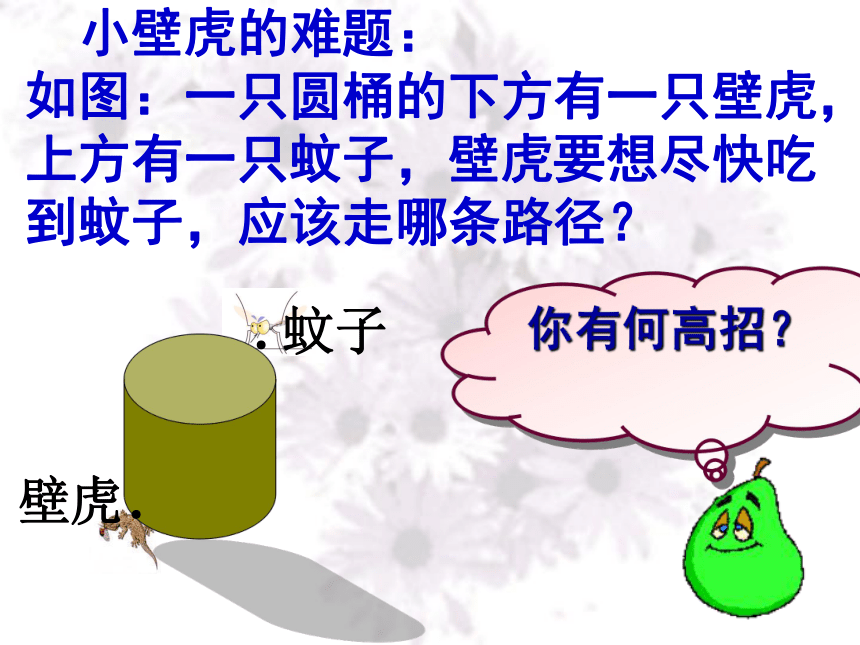
把圆锥、圆柱的侧面展开，会得到什么图形？圆柱圆锥 圆柱的侧面展开图是长方形，圆锥的侧面展开图是扇形 。在实际生活中常常需要了解整个立体图形展开的形状，如包装一个长方体形状的物体，需要根据其平面展开图来裁剪纸张.今天我们要讨论的是一些简单多面体的平面展开图. 仔细观察，下面各种包装盒分别是什么几何体？这些包装盒有什么用呢？你会做这些包装盒吗？如图，上面的图形分别是下面哪个立体图形展开的形状？考考你 小壁虎的难题：
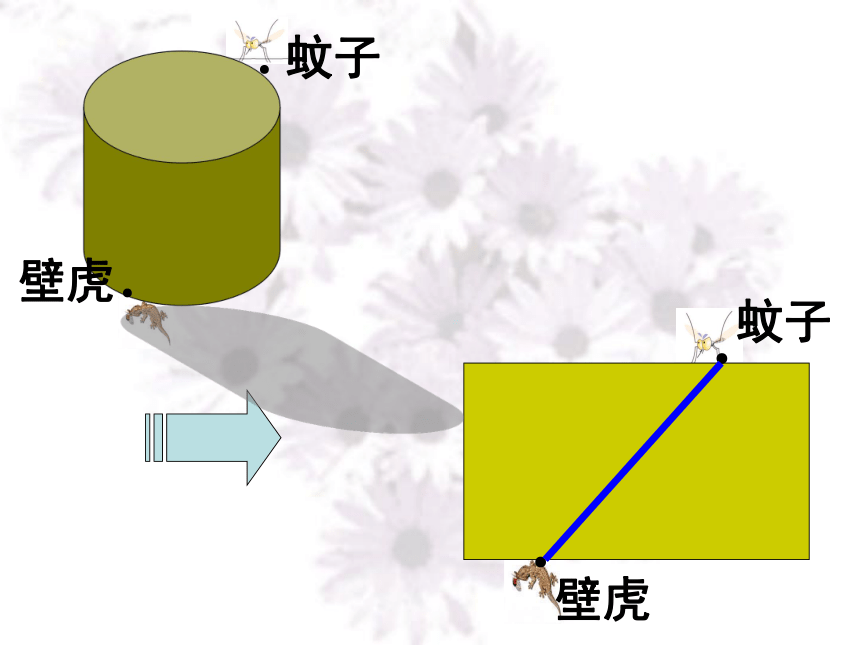
如图：一只圆桶的下方有一只壁虎，上方有一只蚊子，壁虎要想尽快吃到蚊子，应该走哪条路径？你有何高招？ 请一名同学剪开正方体纸盒，铺平，看看它的展开图是由哪些平面图形组成的。小实验探究1:
把一个正方体的表面沿某些棱剪开，展成一个平面图形，能得到哪些平面图形？画出你所得到的展开图请与同伴进行交流。
议一议:怎样把所得到的正方体表面展开图进行分类?
第一类，中间四连方，两侧各一个，共六种。 第二类，中间三连方，两侧各有一、二个，共三种。第三类，中间二连方，两侧各有二个，只有一种。第四类，两排各三个，只有一种。一共十一种记得规律最长两边走，田、凹不能有。（1）（2）下面的图形都是正方体的
展开图吗？（1）（2）（3）右图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学补画的
情况（图中绿色部分），
其中正确的是（ ） A． Ｂ．　 Ｃ．　　 Ｄ．
B长方体 以下哪些图形经过折叠可以围成一个棱柱? ⑴⑵ ⑶⑷想一想、折一折练习巩固：下图中的那些图形可以沿虚线折叠成长方体包装盒，先想一想，再折一折。
下列图形哪个不是长方体的表面展开图？AD C B 把下面的正三角形沿虚线折叠后的几何体是什么？将下图中五角星状的图形沿虚线折叠，得到一个几何体，你在生活中见过和这个几何体形状类似的物体吗？ 下面六个正方形连在一起的图形，经折叠后能围成正方体的图形有哪几个？GFEDCBA如图，这是一个正方体的展开图，如果将它组成原来的正方体，哪些点与点P重合。
有一个正方体，在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色。甲、乙、丙三位同学从三个不同的角度去观察此正方体，结果如下图，问这个正方体各个面的对面的颜色是什么？黑红红兰兰黄黄白绿甲乙丙 有一正方体木块，它的六个面分别标上数字1——6，下图是这个正方体木块从不同面所观察到的数字情况。请问数字1和5对面的数字各是多少？
把左图中长方体的表面展开图，折叠成一个长方体，那么与字母 J重合的点是哪几个？ 多面体(polyhedron)是由平面图形围成的立体图形，沿着多面体的棱将它剪开，可以把多面体变成一个平面图形. 根据正多面体填写下表612826812122222020304结论：面数f +顶点数v -棱数e = 22、下面是一多面体的展开图，平面图形的旁边都标注了字母，请根据要求回答问题：
(1)如果A面在多面体的底部，哪一面会在上面?
(2)如果面F在前面，面B在左面，哪一面会在上面?
(3)如果面C在右面，面D在后面，哪一面会在上面? 本节课你学到了什么?1、 学会了简单几何体（如棱柱，正方体等）的平面展开图，知道按不同的方式展开会得到不同的展开图。2、学会了动手实践，与同学合作。3、友情提醒：不是所有立体图形都有平面展开图，比如球体。下图是一些立体图形的展开图，用它们能围成怎样的立体图形？ 下面请发挥你的聪明才智，与小组内的其他同学合作，设计并制作一个模型，尽可能使设计美观、大方。做一做，比一比。提示：可以是生活中的常用物品，也可以是正方体、长方体、圆柱、圆锥、棱柱、棱锥等几何体或者它们的组合体。