1.1等腰三角形

1.1.1等腰三角形的性质
【学习目标】
1、了解作为证明基础的几条公理的内容，掌握证明的基本步骤和书写格式。
2、经历“探索－发现－猜想－证明”的过程。能够用综合法证明等腰三角形的有关性质定理。
【课前预习】
Ⅰ、预习指导：
1、 前置准备：请你用自己的语言说一说证明的基本步骤。
2、 列举我们已知道的公理：（八年级上p168）
（1）公理：同位角 ，两直线平行。
（2）公理： 的两个三角形全等。（简称 ，字母表示 ）
（3）公理： 的两个三角形全等。 （简称 ，字母表示 ）
（4）公理： 的两个三角形全等。（简称 ，字母表示 ）
Ⅱ、预习自测：
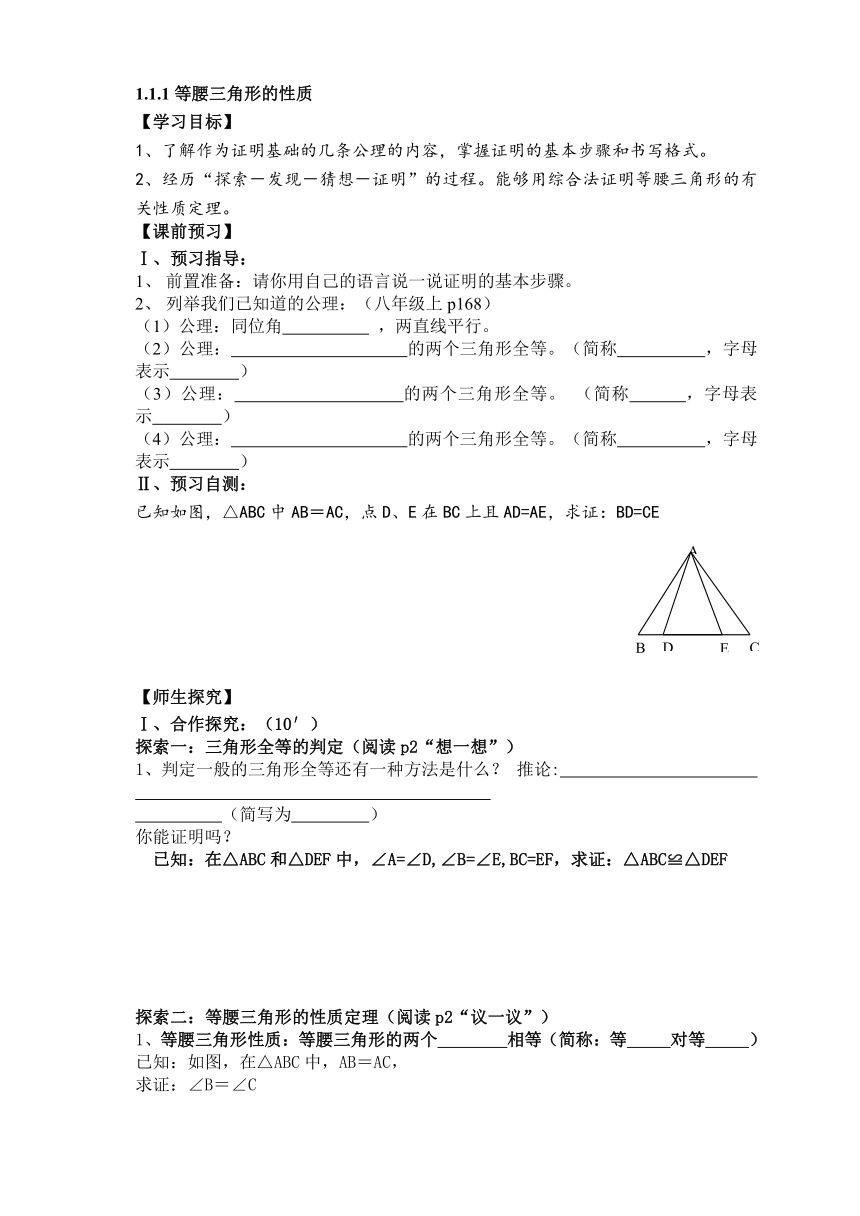
已知如图，△ABC中AB＝AC，点D、E在BC上且AD=AE，求证：BD=CE
【师生探究】
Ⅰ、合作探究：（10′）
探索一：三角形全等的判定（阅读p2“想一想”）
判定一般的三角形全等还有一种方法是什么？ 推论:
（简写为 ）
你能证明吗？
已知：在△ABC和△DEF中，∠A=∠D,∠B=∠E,BC=EF，求证：△ABC≌△DEF
探索二：等腰三角形的性质定理（阅读p2“议一议”）
1、等腰三角形性质：等腰三角形的两个 相等（简称：等 对等 ）
已知：如图，在△ABC中，AB＝AC，
求证：∠B＝∠C
2、推论：等腰三角形的顶角的 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) 、底边上的 、底边上的 互相重合（简称： ）
3、请证明：
推论2：等边三角形的三个角都是 ，并且每个角都等于 。
Ⅱ、自主展示（15′）
Ⅲ、质疑点拨（5′）
Ⅳ、总结归纳（5′）
【当堂检测】（10′）
p3随堂练习
（1）解： (2)解:
2、(1)证明： （2）解：
3、如图，已知：∥，AB=CD，若要使△ABE≌△CDF,仍需添加一个条件，
下列条件中，哪一个不能使△ABE≌△CDF的是（ ）
A、∠A=∠B ; B、BF=CE;
C、AE∥DF; D、AE=DF.
4、P4第3题
Ⅱ、“日日清”
1、（1）某等腰三角形的两条边长分别为3cm和6cm，则它的周长为 。
（2）等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的腰长为 。
2、如图1线段AC与BD交于点O，且OA=OC，请添加一个条件 ，使△OAB≌△OCD
3、如图2，△ABC中AB＝AC，点Ｄ在AC上，且BD=BC=AD，则∠A的度数为
4、已知等腰三角形的两内角的度数之比为1：4，则这个等腰三角形的顶角度数为
5、如图3，A、B、F、D在同一直线上，AB=DF，AE=BC，且AE∥BC。
求证：⑴△AEF≌△BCD，
⑵EF∥CD
A
B
D
E
C
A
B
C
D
图2
D
C
O
A
B
图1
A
B
F
D
E
C
图3