2023-2024学年鲁教版(五四制)数学八年级上册第五章平行四边形回顾与复习(2)学案(无答案)
文档属性
| 名称 | 2023-2024学年鲁教版(五四制)数学八年级上册第五章平行四边形回顾与复习(2)学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 639.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 08:39:09 | ||
图片预览


文档简介
平行四边形复习课(2)
【知识梳理】
知识点一
三角形中位线定理 符号语言:
三角形中位线逆定理 符号语言:
温馨提示:
(1)三角形中位线定理的作用:
位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
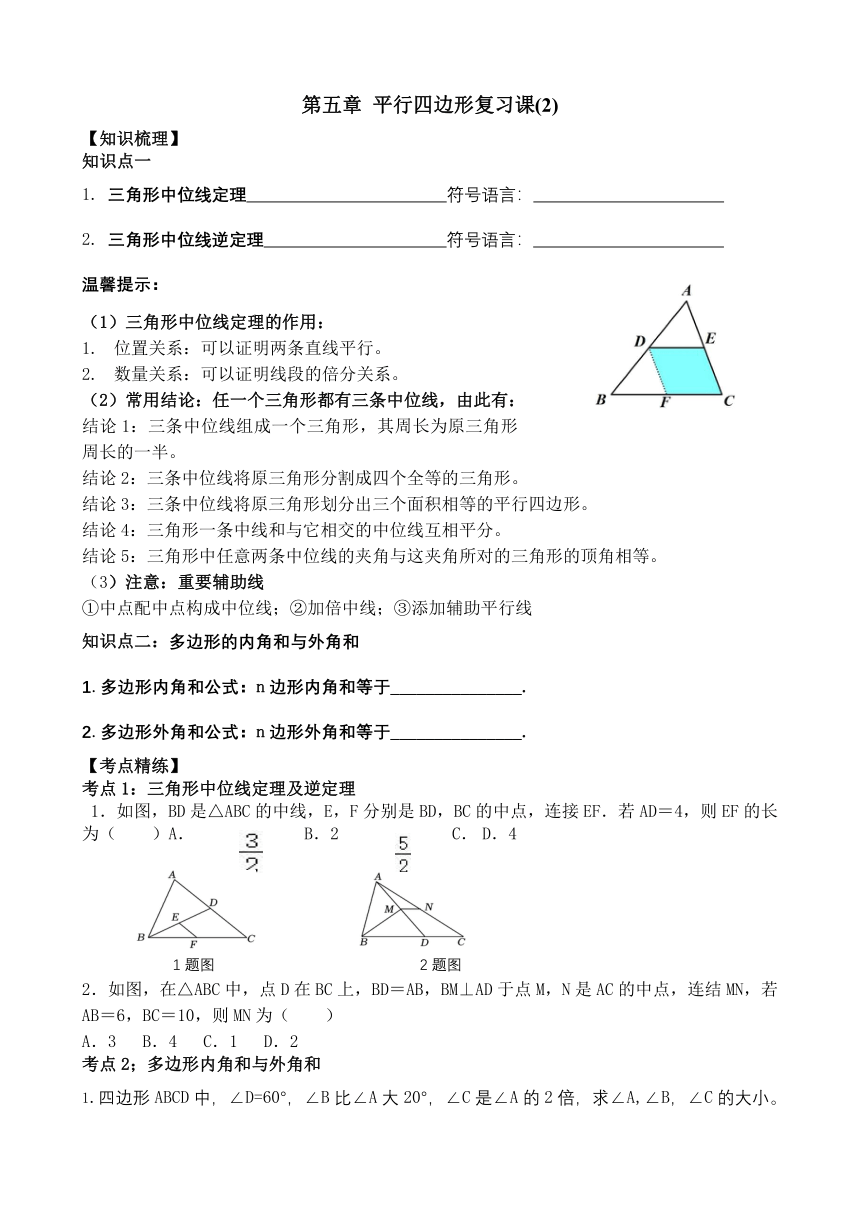
(2)常用结论:任一个三角形都有三条中位线,由此有:
结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形。
结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论5:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等。
(3)注意:重要辅助线
①中点配中点构成中位线;②加倍中线;③添加辅助平行线
知识点二:多边形的内角和与外角和
1.多边形内角和公式:n边形内角和等于_______________.
2.多边形外角和公式:n边形外角和等于_______________.
【考点精练】
考点1:三角形中位线定理及逆定理
1.如图,BD是△ABC的中线,E,F分别是BD,BC的中点,连接EF.若AD=4,则EF的长为( )A. B.2 C. D.4
1题图 2题图
2.如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连结MN,若AB=6,BC=10,则MN为( )
A.3 B.4 C.1 D.2
考点2;多边形内角和与外角和
1.四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小。
2.四边形ABCD中,∠A+∠D=210°,∠ABC与∠BCD的平分线交于点P,求∠P的度数。
【综合测评】 共计100分
选择题(共8小题,每题4分)
1.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
2 B.3 C.4 D.5
1题图 3题图 4题图
2.若一个多边形增加一条边,则它的内角和( )。
A.增加180° B.减少180° C.不变 D.增加360°
3.如图,小林从P点向西直走12m后,向左转,转动的角度为α,再走12m,如此重复,小林共走了108m回到点P,则α=( )A.30° B.40° C.80° D.不存在
4.如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
5.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )A.28 B.14 C.10 D.7
5题图 6题图 7题图
6.如图,在△ABC中,AB=5,AC=11,点D在AC上,若BD=CD=6,AE平分∠BAC,则AE的长为( )A.3 B.4 C.5 D.6
7.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度( )A.保持不变B.逐渐变小C.先变大,再变小 D.逐渐变大
8.如图,依次连接周长为1的小等边三角形各边的中点,得到第二个小等边三角形,再依次连接第二个小等边三角形各边的中点,得到第三个小等边三角形……按这样的规律,第2023个小等边三角形的周长为( )
A. B. C. D.
二、填空题(每小题4分,每题4分)
9.如图,在△ABC中,点D、E分别是AC、BC的中点,以A为圆心,AD为半径作圆弧交AB于点F,若AD=5,DE=4,则BF的值为 .
9题图 10题图 11题图 12题图
10.如图,在四形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,依次连接E、G、F、H得到四边形是 .
11.如图,CD是△ABC的中线,E是CD的中点,F是BE延长线与AC的交点,若AF=2,则AC长为 .
12.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是 .
三、解答题(共4小题,每题13分)
13.在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点E,F分别为BC,AC的中点
求证:DF=BE
14.在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连接DH,则线段DH的长为多少?
15.在△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,求DF的长。
16.(提升题)在四边形ABCD中,AB=CD,点E,F分别是边AD,BC的中点.
(1)如图1,点P为对角线BD的中点,连接PE,PF,若∠PEF=26°,则∠EPF= 128° ;
(2)如图2,直线EF分别与BA,CD的延长线交于点M,N.求证:∠BMF=∠CNF.
【知识梳理】
知识点一
三角形中位线定理 符号语言:
三角形中位线逆定理 符号语言:
温馨提示:
(1)三角形中位线定理的作用:
位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
(2)常用结论:任一个三角形都有三条中位线,由此有:
结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形。
结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论5:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等。
(3)注意:重要辅助线
①中点配中点构成中位线;②加倍中线;③添加辅助平行线
知识点二:多边形的内角和与外角和
1.多边形内角和公式:n边形内角和等于_______________.
2.多边形外角和公式:n边形外角和等于_______________.
【考点精练】
考点1:三角形中位线定理及逆定理
1.如图,BD是△ABC的中线,E,F分别是BD,BC的中点,连接EF.若AD=4,则EF的长为( )A. B.2 C. D.4
1题图 2题图
2.如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连结MN,若AB=6,BC=10,则MN为( )
A.3 B.4 C.1 D.2
考点2;多边形内角和与外角和
1.四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小。
2.四边形ABCD中,∠A+∠D=210°,∠ABC与∠BCD的平分线交于点P,求∠P的度数。
【综合测评】 共计100分
选择题(共8小题,每题4分)
1.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
2 B.3 C.4 D.5
1题图 3题图 4题图
2.若一个多边形增加一条边,则它的内角和( )。
A.增加180° B.减少180° C.不变 D.增加360°
3.如图,小林从P点向西直走12m后,向左转,转动的角度为α,再走12m,如此重复,小林共走了108m回到点P,则α=( )A.30° B.40° C.80° D.不存在
4.如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
5.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )A.28 B.14 C.10 D.7
5题图 6题图 7题图
6.如图,在△ABC中,AB=5,AC=11,点D在AC上,若BD=CD=6,AE平分∠BAC,则AE的长为( )A.3 B.4 C.5 D.6
7.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度( )A.保持不变B.逐渐变小C.先变大,再变小 D.逐渐变大
8.如图,依次连接周长为1的小等边三角形各边的中点,得到第二个小等边三角形,再依次连接第二个小等边三角形各边的中点,得到第三个小等边三角形……按这样的规律,第2023个小等边三角形的周长为( )
A. B. C. D.
二、填空题(每小题4分,每题4分)
9.如图,在△ABC中,点D、E分别是AC、BC的中点,以A为圆心,AD为半径作圆弧交AB于点F,若AD=5,DE=4,则BF的值为 .
9题图 10题图 11题图 12题图
10.如图,在四形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,依次连接E、G、F、H得到四边形是 .
11.如图,CD是△ABC的中线,E是CD的中点,F是BE延长线与AC的交点,若AF=2,则AC长为 .
12.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是 .
三、解答题(共4小题,每题13分)
13.在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点E,F分别为BC,AC的中点
求证:DF=BE
14.在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连接DH,则线段DH的长为多少?
15.在△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,求DF的长。
16.(提升题)在四边形ABCD中,AB=CD,点E,F分别是边AD,BC的中点.
(1)如图1,点P为对角线BD的中点,连接PE,PF,若∠PEF=26°,则∠EPF= 128° ;
(2)如图2,直线EF分别与BA,CD的延长线交于点M,N.求证:∠BMF=∠CNF.
