2023—2024学年苏科版数学八年级上册期中复习卷(无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学八年级上册期中复习卷(无答案) | 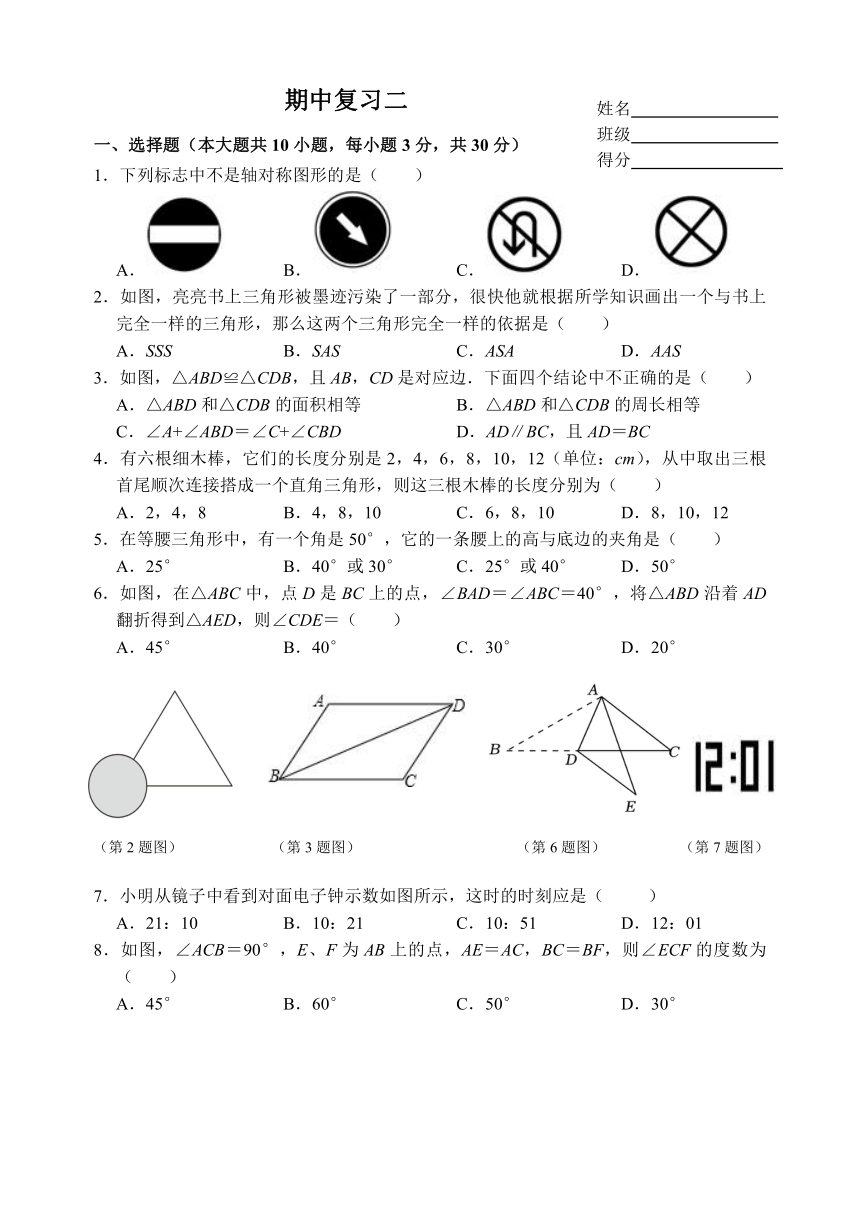 | |
| 格式 | docx | ||
| 文件大小 | 118.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 07:17:15 | ||
图片预览


文档简介
(
姓名
班级
得分
)期中复习二
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列标志中不是轴对称图形的是( )
A. B. C. D.
2.如图,亮亮书上三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.ASA D.AAS
3.如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )
A.△ABD和△CDB的面积相等 B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC
4.有六根细木棒,它们的长度分别是2,4,6,8,10,12(单位:cm),从中取出三根首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
A.2,4,8 B.4,8,10 C.6,8,10 D.8,10,12
5.在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是( )
A.25° B.40°或30° C.25°或40° D.50°
如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=( )
A.45° B.40° C.30° D.20°
(第2题图) (第3题图) (第6题图) (第7题图)
7.小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
A.21:10 B.10:21 C.10:51 D.12:01
8.如图,∠ACB=90°,E、F为AB上的点,AE=AC,BC=BF,则∠ECF的度数为( )
A.45° B.60° C.50° D.30°
(第8题图) (第10题图) (第12题图)
9.△ABC中,AB=13,AC=15,高AD=12,则BC的长为( )
A.14 B.4 C.14或4 D.以上都不对
10.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A.30,2 B.60,2 C.60, D.60,
二.填空题(本大题共8小题,每小题3分,共24分)
11.已知等腰三角形的顶角为80°,那么它的一个底角为 .
12.如图,已知∠1=∠2=90°,AD=AE,那么图中有 对全等三角形.
13.如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长是 cm.
(第13题图) (第14题图) (第15题图)
14.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为 °.
15.如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是 .
16.如图,在△ABC中,AB=AC,BC=BD=ED=EA,求∠A的度数= .
(第16题图) (第17题图) (第18题图)
17.如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为 .
18.如图,在△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB等腰三角形,则符合条件的点P共有 个.
三.解答题(共4小题,共46分)
19.(10分)如图,A、B、C三家公司设想共建一个污水处理站M,使得该站到B、C两公司的距离相等,且使A公司到污水处理站M的管线最短,试确定这污水处理站M的位置.(不写作法,保留作图痕迹)
20(12分).如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:△CEB≌△ADC;
(2)若AD=2.5cm,DE=1.7cm,求BE的长.
21.(12分)我们规定:三角形任意两边的“极化值”等于第三边上的中线与第三边一半的平方差.如图,在△ABC中,OA是边BC上的中线,AB与AC的“极化值”就等于OA2﹣OB2的值,可理解为AB△AC=AO2﹣BO2.若∠BAC=90°,AB=8,AC=6,OA是边BC上的中线,求下面式子的值:
(1)AB△AC;
(2)OC△OA.
22.(12分)如图①△ABC是正三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N,连接MN.
(1)探究BM、MN、NC之间的关系,并说明理由.
(2)若△ABC的边长为2,求△AMN的周长.
(3)若点M、N分别是AB、CA延长线上的点,其它条件不变,在图②中画出图形,并说出BM、MN、NC之间的关系.
姓名
班级
得分
)期中复习二
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列标志中不是轴对称图形的是( )
A. B. C. D.
2.如图,亮亮书上三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.ASA D.AAS
3.如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )
A.△ABD和△CDB的面积相等 B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC
4.有六根细木棒,它们的长度分别是2,4,6,8,10,12(单位:cm),从中取出三根首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
A.2,4,8 B.4,8,10 C.6,8,10 D.8,10,12
5.在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是( )
A.25° B.40°或30° C.25°或40° D.50°
如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=( )
A.45° B.40° C.30° D.20°
(第2题图) (第3题图) (第6题图) (第7题图)
7.小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
A.21:10 B.10:21 C.10:51 D.12:01
8.如图,∠ACB=90°,E、F为AB上的点,AE=AC,BC=BF,则∠ECF的度数为( )
A.45° B.60° C.50° D.30°
(第8题图) (第10题图) (第12题图)
9.△ABC中,AB=13,AC=15,高AD=12,则BC的长为( )
A.14 B.4 C.14或4 D.以上都不对
10.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A.30,2 B.60,2 C.60, D.60,
二.填空题(本大题共8小题,每小题3分,共24分)
11.已知等腰三角形的顶角为80°,那么它的一个底角为 .
12.如图,已知∠1=∠2=90°,AD=AE,那么图中有 对全等三角形.
13.如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长是 cm.
(第13题图) (第14题图) (第15题图)
14.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为 °.
15.如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是 .
16.如图,在△ABC中,AB=AC,BC=BD=ED=EA,求∠A的度数= .
(第16题图) (第17题图) (第18题图)
17.如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为 .
18.如图,在△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB等腰三角形,则符合条件的点P共有 个.
三.解答题(共4小题,共46分)
19.(10分)如图,A、B、C三家公司设想共建一个污水处理站M,使得该站到B、C两公司的距离相等,且使A公司到污水处理站M的管线最短,试确定这污水处理站M的位置.(不写作法,保留作图痕迹)
20(12分).如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:△CEB≌△ADC;
(2)若AD=2.5cm,DE=1.7cm,求BE的长.
21.(12分)我们规定:三角形任意两边的“极化值”等于第三边上的中线与第三边一半的平方差.如图,在△ABC中,OA是边BC上的中线,AB与AC的“极化值”就等于OA2﹣OB2的值,可理解为AB△AC=AO2﹣BO2.若∠BAC=90°,AB=8,AC=6,OA是边BC上的中线,求下面式子的值:
(1)AB△AC;
(2)OC△OA.
22.(12分)如图①△ABC是正三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N,连接MN.
(1)探究BM、MN、NC之间的关系,并说明理由.
(2)若△ABC的边长为2,求△AMN的周长.
(3)若点M、N分别是AB、CA延长线上的点,其它条件不变,在图②中画出图形,并说出BM、MN、NC之间的关系.
同课章节目录
