2023-—2024学年鲁教版(五四制)数学八年级上册4.4.2图形变化的简单应用(2)学案(无答案)
文档属性
| 名称 | 2023-—2024学年鲁教版(五四制)数学八年级上册4.4.2图形变化的简单应用(2)学案(无答案) | 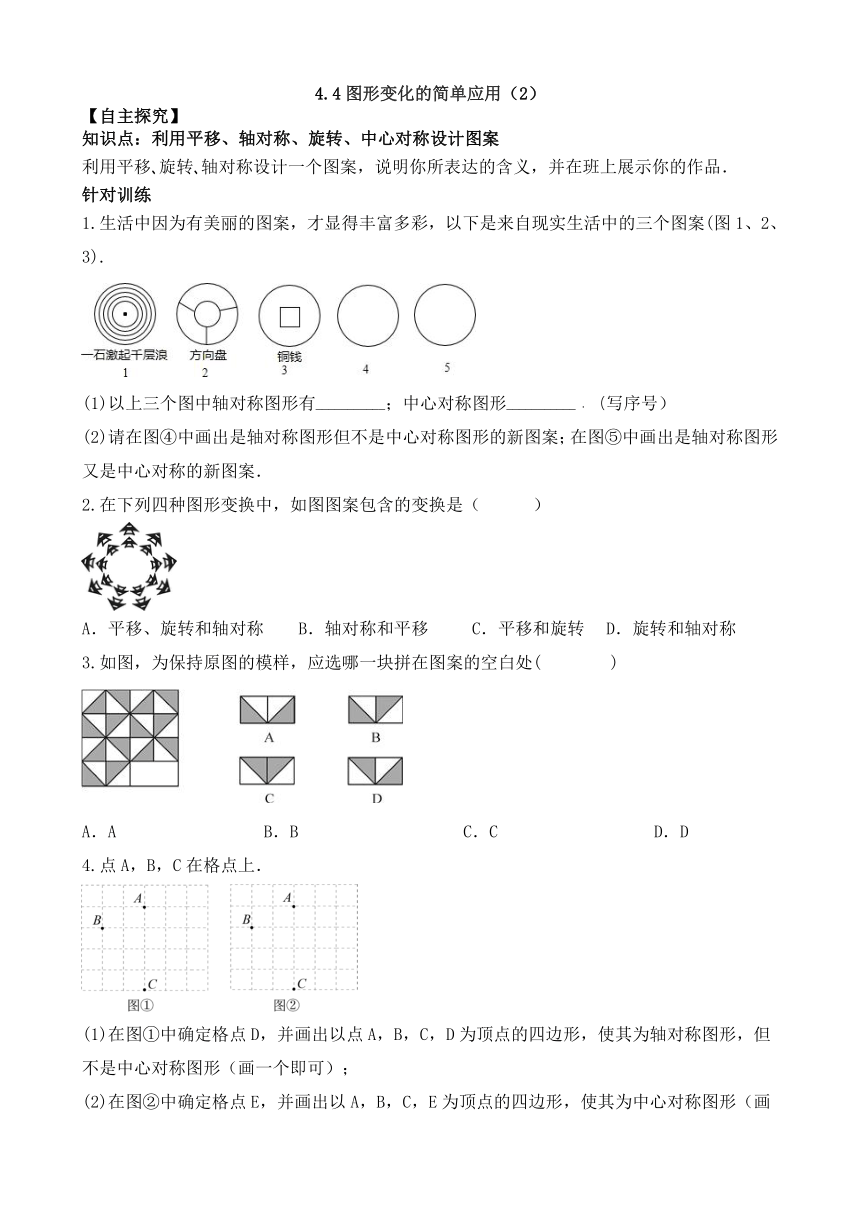 | |
| 格式 | docx | ||
| 文件大小 | 336.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 08:59:32 | ||
图片预览


文档简介
4.4图形变化的简单应用(2)
【自主探究】
知识点:利用平移、轴对称、旋转、中心对称设计图案
利用平移 旋转 轴对称设计一个图案,说明你所表达的含义,并在班上展示你的作品.
针对训练
1.生活中因为有美丽的图案,才显得丰富多彩,以下是来自现实生活中的三个图案(图1、2、3).
(1)以上三个图中轴对称图形有___________;中心对称图形___________.(写序号)
(2)请在图④中画出是轴对称图形但不是中心对称图形的新图案;在图⑤中画出是轴对称图形又是中心对称的新图案.
2.在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移 C.平移和旋转 D.旋转和轴对称
3.如图,为保持原图的模样,应选哪一块拼在图案的空白处( )
A.A B.B C.C D.D
4.点A,B,C在格点上.
(1)在图①中确定格点D,并画出以点A,B,C,D为顶点的四边形,使其为轴对称图形,但不是中心对称图形(画一个即可);
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).
5.如图,下列4×4网格图都是由16个相同的小正方形组成,每个网格图中有4个小正方形已涂上阴影,请你在空白小正方形中,按下列要求涂上阴影:
(1)在图1中选取1个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
【基础巩固】
1.如图所示图案分别是汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2.下列图形均可由“基本图案”通过变换得到:(只填序号)
(1)可以平移但不能旋转的是 ;
(2)可以旋转但不能平移的是 ;
(3)既可以平移,也可以旋转的是 .
3.请认真观察图(1)的4个图中阴影部分构成的图案,回答下列问题:
请写出这四个图案都具有的两个共同特征:特征1: ;特征2:
(2)请在图(2)中设计出你心中最美的图案,使它也具备你所写出的上述特征(用阴影表示).
4.在平面直角坐标系中,将坐标为(0,0),(1,3),(2,0),(3,3)的点用线段依次连接起来得到一个图案N.
(1)在图(1)中,分别画出图案N关于x轴和y轴对称的图案;
(2)在图(2)中,将图案N先向左平移3个单位长度,再向下平移4个单位长度,画出第二次平移后的图案;
(3)在图(3)中,以原点为对称中心,画出与图案N成中心对称的图案.
【素养提优】
下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.
请将“弦图”中的四个直角三角形通过你所学过的图形变换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠;(2)所设计的图案(不含方格纸)必须一个是中心对称图形,另一个是轴对称图形.
【中考链接】
(2018·宁波)如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有 种不同的涂法.
【方法提炼】
利用平移、轴对称、旋转、中心对称设计图案,解题的关键是掌握轴对称图形、旋转和中心对称图形的概念.
【达标测评】(共10分)(教师寄语:自信源于实力!)总得分:__________
1.(2分)在下列四个图案中,既包含图形的旋转,又有图形的轴对称设计的是( )
A. B. C. D.
2.(3分)如图所示,图形(1)经过 变换成图形(2),图形(2)经过 变换成图形(3),图形(3)经过 变换成图形(4).
3.(2分)如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是 (请填写正确答案的序号)
①黑(1,5),白(5,5); ②黑(3,2),白(3,3);
③黑(3,3),白(3,1); ④黑(3,1),白(3,3)
4.(3分)图①、图②均是6×5的正方形网格,每个小正方形的顶点称为格点,点A、B、C均在格点上,在给定的网格中按要求画图.要求:
(1)在图①中画一个BCD,使△DBC≌ABC全等;
(2)在图②中画一个ACE使它与ABC全等.
【自主探究】
知识点:利用平移、轴对称、旋转、中心对称设计图案
利用平移 旋转 轴对称设计一个图案,说明你所表达的含义,并在班上展示你的作品.
针对训练
1.生活中因为有美丽的图案,才显得丰富多彩,以下是来自现实生活中的三个图案(图1、2、3).
(1)以上三个图中轴对称图形有___________;中心对称图形___________.(写序号)
(2)请在图④中画出是轴对称图形但不是中心对称图形的新图案;在图⑤中画出是轴对称图形又是中心对称的新图案.
2.在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移 C.平移和旋转 D.旋转和轴对称
3.如图,为保持原图的模样,应选哪一块拼在图案的空白处( )
A.A B.B C.C D.D
4.点A,B,C在格点上.
(1)在图①中确定格点D,并画出以点A,B,C,D为顶点的四边形,使其为轴对称图形,但不是中心对称图形(画一个即可);
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).
5.如图,下列4×4网格图都是由16个相同的小正方形组成,每个网格图中有4个小正方形已涂上阴影,请你在空白小正方形中,按下列要求涂上阴影:
(1)在图1中选取1个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
【基础巩固】
1.如图所示图案分别是汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2.下列图形均可由“基本图案”通过变换得到:(只填序号)
(1)可以平移但不能旋转的是 ;
(2)可以旋转但不能平移的是 ;
(3)既可以平移,也可以旋转的是 .
3.请认真观察图(1)的4个图中阴影部分构成的图案,回答下列问题:
请写出这四个图案都具有的两个共同特征:特征1: ;特征2:
(2)请在图(2)中设计出你心中最美的图案,使它也具备你所写出的上述特征(用阴影表示).
4.在平面直角坐标系中,将坐标为(0,0),(1,3),(2,0),(3,3)的点用线段依次连接起来得到一个图案N.
(1)在图(1)中,分别画出图案N关于x轴和y轴对称的图案;
(2)在图(2)中,将图案N先向左平移3个单位长度,再向下平移4个单位长度,画出第二次平移后的图案;
(3)在图(3)中,以原点为对称中心,画出与图案N成中心对称的图案.
【素养提优】
下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.
请将“弦图”中的四个直角三角形通过你所学过的图形变换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠;(2)所设计的图案(不含方格纸)必须一个是中心对称图形,另一个是轴对称图形.
【中考链接】
(2018·宁波)如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有 种不同的涂法.
【方法提炼】
利用平移、轴对称、旋转、中心对称设计图案,解题的关键是掌握轴对称图形、旋转和中心对称图形的概念.
【达标测评】(共10分)(教师寄语:自信源于实力!)总得分:__________
1.(2分)在下列四个图案中,既包含图形的旋转,又有图形的轴对称设计的是( )
A. B. C. D.
2.(3分)如图所示,图形(1)经过 变换成图形(2),图形(2)经过 变换成图形(3),图形(3)经过 变换成图形(4).
3.(2分)如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是 (请填写正确答案的序号)
①黑(1,5),白(5,5); ②黑(3,2),白(3,3);
③黑(3,3),白(3,1); ④黑(3,1),白(3,3)
4.(3分)图①、图②均是6×5的正方形网格,每个小正方形的顶点称为格点,点A、B、C均在格点上,在给定的网格中按要求画图.要求:
(1)在图①中画一个BCD,使△DBC≌ABC全等;
(2)在图②中画一个ACE使它与ABC全等.
